1
На каком из следующих рисунков больше всего треугольников?

2
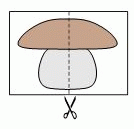
Арик разрезал следующий рисунок пополам и переложил две половинки. Что у него могло получиться?

3
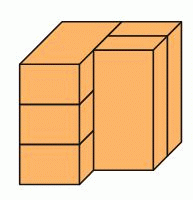
Фигура на рисунке состоит из пяти одинаковых кирпичей. Сколько из этих кирпичей касаются ровно трёх других кирпичей?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
4
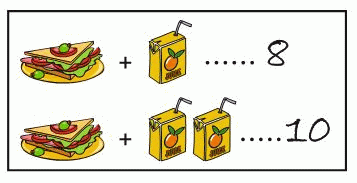
Сэндвич и сок стоят 8 рублей. Сэндвич и два сока стоят 10 рублей. Сколько стоит один сок?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
5
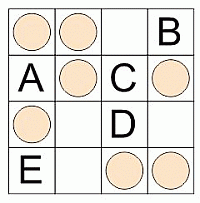
На некоторых клетках таблицы находятся монеты. На какую клетку нужно положить ещё одну монету так, чтобы в каждой строчке и в каждом столбце таблицы было ровно по 2 монеты?
A) A Б) B В) C Г) D Д) E
6
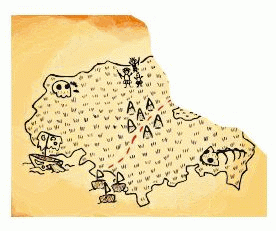
Обезьянка оторвала кусок от карты капитана Джека. Каким может быть этот кусок?

7

Петя сложил квадрат из четырёх плиток пазла на рисунке. Какой квадрат у него получился?

8

На клетчатый лист бумаги разлились чернила, как показано на рисунке. Сколько клеток оказались (частично или полностью) залиты чернилами?
A) 16 Б) 17 В) 18 Г) 19 Д) 20
9

Кенгуру написал число, а затем накрыл цифры фигурками (одинаковые цифры – одинаковыми фигурками, а разные разными). Каким из следующих чисел может быть число, написанное Кенгуру?
A) 34426 Б) 34526 В) 34423 Г) 34424 Д) 32446
10

В каждой из следующих корзин спит по одному зверьку. Медвежонок и лисёнок спят в корзинах одинаковой формы с одинаковым узором. У Кенгурёнка и котёнка одинаковый узор на корзинках. В какой корзине спит щенок?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
11
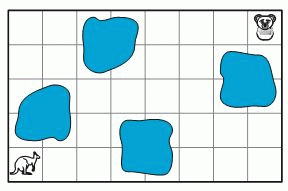
Кенгуру хочет пройти до клетки с коалой по неокрашенным клеткам. Какой путь ему следует выбрать?
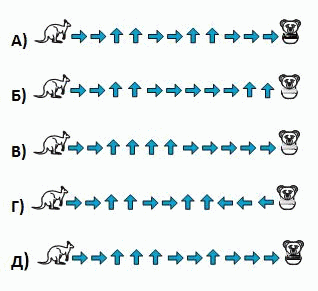
12
Вася сложил 5 зверюшек из геометрических фигур. Одна из таких фигур есть только у одной зверюшки. У какой?
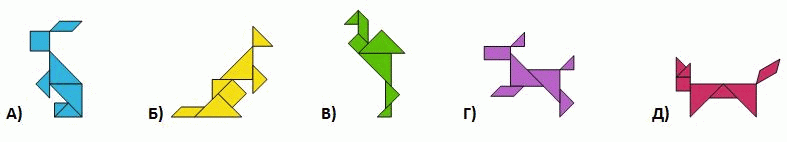
13
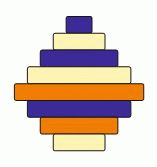
Какой вид сверху имеет следующая пирамидка, сложенная из разноцветных дисков?

14
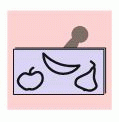
Какой отпечаток делает штамп на рисунке сверху?

15
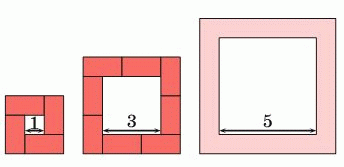
Катя строит вокруг квадратов «забор» из доминошек, состоящих из двух клеток со стороной 1, как показано на рисунке. Сколько доминошек ей понадобится, чтобы построить «забор» вокруг квадрата со стороной 5?
A) 10 Б) 11 В) 12 Г) 14 Д) 16
16
У Ани есть стикеры:

Она клеит их друг на друга. Звезду она наклеила после квадрата, но до того, как наклеила треугольник. Что у неё могло получиться в результате?

17
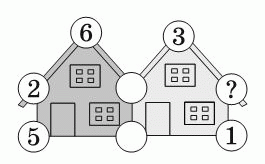
Сумма чисел в кружочках на краях каждого домика равна 20. Некоторые из этих чисел указаны на рисунке. Какое число должно быть в кружочке, отмеченном знаком вопроса?
A) 3 Б) 4 В) 7 Г) 9 Д) 14
18
На следующих рисунках изображены газоны. Какой из них самый маленький?

19
Каждый год Марии на день рождения дарили плюшевых мишек. На свой первый день рождения ей подарили 1 мишку, на второй – 2 мишки. На каждый следующий день рождения она получала на одного мишку больше, чем на предыдущий день рождения. Сколько всего плюшевых мишек подарили Марии за первые 6 лет?
A) 19 Б) 20 В) 21 Г) 22 Д) 23
20
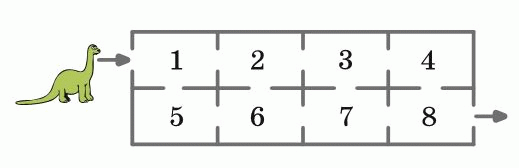
Дино идет сквозь здание от входа к выходу. Через каждую комнату он может пройти не более чем один раз. Проходя через комнаты, Дино складывает номера комнат. Какая наибольшая сумма может получиться у Дино, когда он выйдет из здания?
A) 27 Б) 29 В) 32 Г) 34 Д) 36
21
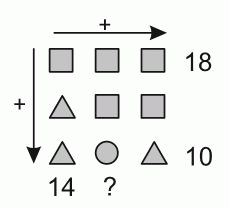
На рисунке фигуры обозначают числа (одинаковые фигуры – одинаковые числа, разные фигуры – разные числа). Суммы чисел в двух строчках и в одном столбце указаны. Чему равна сумма чисел в среднем столбце?
A) 10 Б) 12 В) 14 Г) 16 Д) 18
22
На конкурсе красоты участвуют три зебры. Побеждает та, у которой больше всего полос. У Руны 15 полос, а у Зары на 3 полосы больше. У Руны на 5 полос меньше, чем у Бибы. Сколько полос у победительницы?
A) 16 Б) 18 В) 20 Г) 22 Д) 24
23
Автомобиль Кенги может поворачивать только налево, но не может поворачивать направо. Какой из следующих маршрутов может быть маршрутом Кенги?

24

В ряд расположено пять карт так, как показано на рисунке. За один ход можно поменять местами любые две карты. За какое наименьшее число ходов можно расположить карты так, чтобы числа на них шли в порядке возрастания?
A) 1 Б) 2 В) 3 Г) 4 Д) 5