1
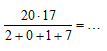
A) 3,4 Б) 17 В) 34 Г) 201,7 Д) 340
2
Вася любит строить модели машин в масштабе 1 : 87. Он даже построил модель автомобиля своего папы. Длина модели оказалась равной 5 см. Чему равна действительная длина автомобиля Васиного папы?
A) 4,35 м Б) 4,55 м В) 4,75 м Г) 4,85 м Д) 5,22 м
3
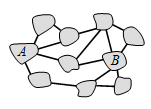
На рисунке показаны 10 островов, соединённых 15 мостами. Какое наименьшее число мостов нужно закрыть, чтобы нельзя было добраться по мостам от острова A до острова B?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
4
Известно, что 75% числа a равны 40% числа b. Это означает, что …
A) 15a = 8b
Б) 7a = 8b
В) 3a = 2b
Г) 5a = 12b
Д) 8a = 5b
5
Четыре из следующих рисунков являются фрагментами графика одной и той же квадратичной функции. Какой из рисунков не является фрагментом этой функции?
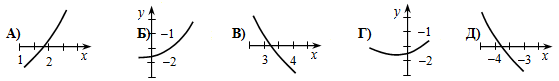
6
Дан круг с центром O. Отрезки AB и CX – его диаметры, OB = BC (см. рис.). Какая (по площади) часть этого круга заштрихована?
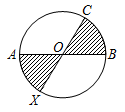
A) 2/5 Б) 1/3 В) 2/7 Г) 3/8 Д) 4/11
7
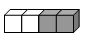
Брусок склеен из двух белых и двух серых кубиков как показано на рисунке выше. Какой из следующих параллелепипедов можно построить из четырёх таких брусков?
8
Какая четверть координатной плоскости не содержит точек графика функции y = -3,5x + 7?
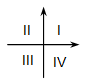
A) I
Б) II
В) III
Г) IV
Д) такой четверти нет
9
В следующих пяти коробках находятся синие и красные шары, как указывают надписи. Из какой коробки вероятность достать наугад синий шар является наибольшей?
10
График какой из следующих функций имеет больше всего общих точек с графиком y = x?
A) y = x2
Б) y = x3
В) y = x4
Г) y = -x4
Д) y = -x
11
Три попарно касающиеся окружности с центрами A, B и C имеют радиусы 3, 2 и 1 соответственно. Чему равна площадь треугольника ABC?
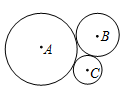
A) 6
Б) 4√3
В) 3√2
Г) 9
Д) 2√6
12
Числа p и q такие, что 0 < p < 1 < q. Какое из следующих выражений имеет наибольшее значение?
A) pq
Б) p + q
В) p : q
Г) p
Д) q
13
Два цилиндра A и B имеют одинаковый объем. Радиус основания у цилиндра B на 10% больше, чем у цилиндра A. На сколько высота цилиндра A больше высоты цилиндра B?
A) на 5%
Б) на 10%
В) на 11%
Г) на 20%
Д) на 21%
14
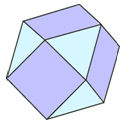
Многогранник на рисунке имеет только треугольные и квадратные грани. Каждая квадратная грань окружена четырьмя треугольными, а каждая треугольная грань окружена тремя квадратными. Количество квадратных граней равно 6. Сколько треугольных граней имеет данный многогранник?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
15
Имеется четыре одинаковых правильных тетраэдра. На гранях каждого тетраэдра записаны цифры 2, 0, 1 и 7. Если подбросить все 4 тетраэдра (как игральные кубики), то какова вероятность того, что они выпадут так, что можно будет составить число 2017, используя ровно одну из трёх видимых цифр каждого тетраэдра?
A) 1/256 Б) 63/64 В) 81/256 Г) 3/32 Д) 29/32
16
Коэффициенты a и b многочлена 5x3 + ax2 + bx + 24 являются целыми числами. Какое из следующих чисел заведомо не может быть корнем этого многочлена?
A) 1 Б) -1 В) 3 Г) 5 Д) 6
17
У Юли есть 2017 фишек, 1009 из них – чёрные, а остальные – белые. Она решила сложить из фишек квадрат наибольших размеров так, чтобы цвета фишек чередовались, как показано на рисунке. В левом верхнем углу она положила чёрную фишку. Сколько фишек каждого цвета у Юли останется?
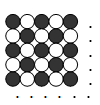
A) ни одной
Б) по 40
В) по 41
Г) 40 чёрных и 41 белая
Д) 40 белых и 41 чёрная
18
Два последовательных натуральных числа таковы, что сумма цифр каждого из них делится на 7. Из какого наименьшего числа цифр состоит меньшее из этих двух чисел?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
19
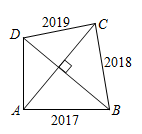
В выпуклом четырёхугольнике ABCD диагонали перпендикулярны. Длины трёх сторон указаны на рисунке. Найдите длину четвёртой стороны.
A) 2016
Б) 2018
В) √20202 - 4
Г) √20182 + 2
Д) 2020
20
Тутти старается быть хорошим кенгурёнком, но очень любит приврать для забавы. Поэтому каждое третье его утверждение ложно, а остальные – правдивы. Иногда он начинает с ложного утверждения, иногда с одного или двух правдивых. Тутти задумал двузначное число и сообщил о нём своему другу следующее:
1) «одна из цифр этого числа – цифра 2»
2) «это число больше 50»
3) «оно чётное»
4) «это число меньше 30»
5) «оно делится на 3»
6) «одна цифр этого числа – цифра 7»
Чему равна сумма цифр числа, задуманного Тутти?
A) 9 Б) 12 В) 13 Г) 15 Д) 17
21
Сколько натуральных чисел обладает свойством: если у данного числа стереть последнюю цифру, то полученное число будет в 14 раз меньше исходного?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
22
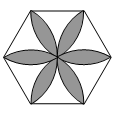
На рисунке изображён правильный шестиугольник со стороной 1. Цветок построен с помощью дуг окружностей радиуса 1 с центрами в вершинах данного шестиугольника. Чему равна площадь цветка?
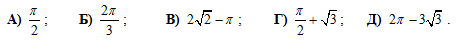
23
Последовательность an задана следующим образом: a1 = 2017 и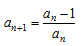 
для всех n≥1. Тогда a2017 = ...
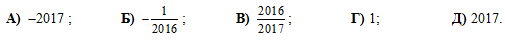
24
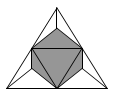
Из правильного тетраэдра вырезали четыре угла по плоскостям, проходящим через середины соседних рёбер. Какую часть от объема исходного тетраэдра составляет объем полученного тела?
A) 4/5 Б) 3/4 В) 2/3 Г) 1/2 Д) 1/3
25
Периметр прямоугольного треугольника равен 18, а сумма квадратов его сторон равна 128. Чему равна площадь этого треугольника?
A) 18 Б) 16 В) 12 Г) 10 Д) 9
26
У вас есть 5 коробок, 5 белых шаров и 5 чёрных шаров. Вы выбираете, как разложить шары по коробкам (в каждую коробку нужно положить хотя бы один шар). Ваш оппонент выбирает коробку и вытаскивает, не глядя, один шар. Он выигрывает, если этот шар окажется белым, в противном случае выигрываете вы. Как вам следует разложить шары по коробкам, чтобы иметь наибольшие шансы выиграть?
A) по одному белому и чёрному шару в каждую коробку
Б) все чёрные шары в 3 коробки и все белые в две коробки
В) все чёрные шары в 4 коробки и все белые в одну коробку
Г) по одному чёрному шару в каждую коробку и все белые в одну из них
Д) по одному белому шару в каждую коробку и все чёрные в одну из них
27
Девять целых чисел вписали в таблицу 3 × 3. Сумма всех вписанных чисел равна 500, любые два числа в соседних по стороне клетках отличаются на 1. Какое число вписано в центральную клетку?
A) 50 Б) 54 В) 55 Г) 56 Д) 57
28
Если |x| + x + y = 5 и x + |y| - y = 10, то x + y = ...
A) 1 Б) 2 В) 3 Г) 4 Д) 5
29
Сколько существует трёхзначных чисел abc, таких, что (a + b)c есть трёхзначное число, которое является степенью числа 2?
A) 15 Б) 16 В) 18 Г) 20 Д) 21
30
Каждый из 2017 жителей острова либо лжец (всегда лжёт), либо правдивый (всегда говорит правду). Более 1000 островитян приняли участие в банкете и уселись за одним большим круглым столом. Каждый из них сказал: «Один из моих соседей, сидящих рядом, лжец, а другой – правдивый». Какое наибольшее число правдивых может быть на этом острове?
A) 1683 Б) 668 В) 670 Г) 1344 Д) 1343