1
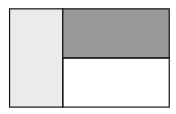
Флаг Кенгуру – прямоугольник, состоящий из трёх равных прямоугольников (см. рис.). Как относятся ширина и длина флага?
A) 1 : 2
Б) 1 : 3
В) 2 : 3
Г) 3 : 4
Д) 2 : 5
2

В клетки таблицы 2×2 вписаны числа 1, 2, 3 и 4. Затем были подсчитаны суммы чисел в строчках и столбцах. Две из этих сумм оказались равны 4 и 5. Чему равны две другие суммы?
A) 6 и 6
Б) 3 и 5
В) 4 и 5
Г) 4 и 6
Д) 5 и 6
3
Прямоугольник был окрашен несколькими способами так, как показано ниже. В каком из вариантов ответа площадь серой части наибольшая?

4

Три треугольника соединены так, как показано на рисунке. В каком из следующих ответов эти три треугольника соединены так же?

5
У пирамиды 23 грани. Сколько у этой пирамиды рёбер?
A) 23 Б) 24 В) 44 Г) 48 Д) 69
6
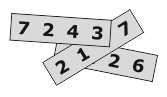
На каждой из трёх полосок бумаги написано четырёхзначное число (см. рис.). Сумма этих трёх чисел равна 11126. Три цифры скрыты. Какие это цифры?
A) 1, 4 и 6
Б) 1, 5 и 7
В) 3, 3 и 3
Г) 4, 5 и 6
Д) 4, 5 и 7
7
Чему равна первая (слева) цифра наименьшего числа, сумма цифр которого равна 2019?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
8
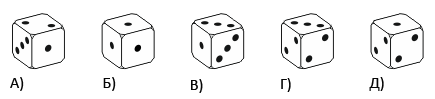
На рёбрах кубика отмечены 1, 2 или 3 точки так, что вероятность выпадения 1 равна 1/2, а вероятность выпадения 2 равна 1/3. Каким из следующих не может быть такой кубик?
9
Миша изобрёл новую операцию:
x * y = y – x.
Если числа a, b, с удовлетворяют равенству
(a * b) * c = a * (b * c),
то какое из следующих равенств заведомо верно?
A) a = b
Б) b = c
В) a = c
Г) a = 0
Д) c = 0
10
Сколько натуральных чисел от 210 до 213 включительно делятся на 210?
A) 2 Б) 4 В) 6 Г) 8 Д) 16
11
На какую наибольшую степень числа 3 делится (7! + 8! + 9!)? (n! = 1 • 2 • 3 • … • n)
A) 32 Б) 34 В) 35 Г) 36 Д) другой ответ
12
В этом году число юношей в моём классе увеличилось на 20%, а число девушек уменьшилось на 20%. В результате, на одного учащегося стало больше. Какое из следующих чисел может быть числом учащихся в моём классе теперь?
A) 22 Б) 26 В) 29 Г) 31 Д) 34
13
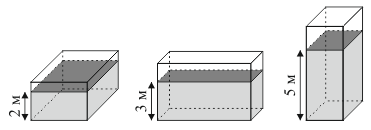
Одинаковые сосуды, имеющие форму прямоугольного параллелепипеда, частично наполнены 120 м3 воды. Уровни воды в зависимости от того, какая грань является основанием сосуда, показаны на рисунке. Чему равен объем сосуда?
A) 100 м3
Б) 180 м3
В) 200 м3
Г) 220 м3
Д) 240 м3
14
Три кенгуру Алекс, Боб и Карл ходят на прогулку каждый день. Если Алекс гуляет без шляпы, то Боб гуляет в шляпе. А если Боб гуляет без шляпы, то Карл гуляет в шляпе. Сегодня Карл гуляет без шляпы. Кто из них наверняка сегодня гуляет в шляпе?
A) только Алекс или Боб
Б) только Алекс
В) любой из них
Г) не Алекс и не Боб
Д) только Боб
15
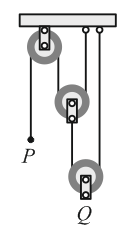
Система на рисунке состоит из трёх блоков с вертикальными верёвками. На сколько см поднимется вверх блок Q, если потянуть за конец верёвки P вниз на 24 см?
A) 24 Б) 12 В) 8 Г) 6 Д) 24/5
16
Будем называть натуральное число n хорошим, если наибольший делитель n (исключая само n) равен n – 6. Сколько существует хороших чисел?
A) 1 Б) 2 В) 3 Г) 6 Д) бесконечно много
17
Из вершин n-угольника случайным образом выбирают две вершины. Вероятность того, что выбранные вершины являются концами диагонали, равна 0,8. Чему равно n?
A) 8 Б) 9 В) 10 Г) 11 Д) 12
18
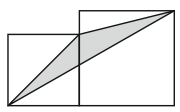
Два квадрата со сторонами a и b (a < b) расположены так, как показано на рисунке. Найдите площадь заштрихованного треугольника.
19
Чему равна целая часть числа 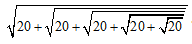 ?
?
A) 4 Б) 5 В) 6 Г) 20 Д) 25
20
Света делила на калькуляторе (a + b) на с (a, b и с – натуральные числа). Она получила a + b : c = 11. А также она получила что, b + a : c = 14. Света поняла, что калькулятор сначала выполняет деление, а потом сложение. Чему равно значение (a + b) : c?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
21
Пусть a – сумма всех натуральных делителей числа 1024, а b – произведение всех этих делителей. Тогда
A) (a – 1)5 = b
Б) (a + 1)5 = b
В) a5 = b
Г) a5 – 1 = b
Д) a5 + 1 = b
22
При каких значениях параметра a уравнение 2 – |x| = ax имеет ровно два решения?
A) (–∞; –1]
Б) (–1; –1)
В) [1; +∞)
Г) {0}
Д) {–1; 0,1}
23
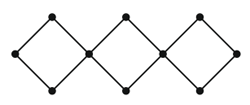
Вершины квадратов на рисунке пронумерованы числами от 1 да 10 так, что суммы чисел в вершинах всех трёх квадратов одинаковы. Какое наименьшее значение может иметь эта сумма?
A) 18 Б) 19 В) 20 Г) 21 Д) 22
24
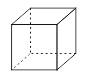
Сколько различных плоскостей проходят, по крайней мере, через три вершины данного куба?
A) 6 Б) 8 В) 12 Г) 16 Д) 20
25
Парабола y = x2 – 2 пересекается в восьми точках с четырьмя прямыми, проходящими через начало координат. Каким может быть произведение абсцисс всех восьми точек пересечения?
A) только 16
Б) только –16
В) только 8
Г) только –8
Д) возможны несколько различных значений
26
Сколько существует различных целых n, при которых |n2 – 2n – 3| является простым числом?
A) 1 Б) 2 В) 3 Г) 4 Д) бесконечно много
27
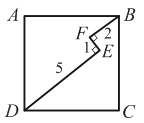
Ломаная DEFB лежит внутри квадрата ABCD. EF ⊥ FB, DE ⊥ EF, FB = 2, EF = 1, DE = 5. Чему равна длина стороны данного квадрата?
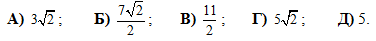
28
Последовательность a1, a2, a3, … начинается с a1 = 49. Каждый следующий член равен квадрату увеличенной на 1 суммы цифр предыдущего члена. Например,
a2 = (4 + 9 + 1)2 = 196. Чему равно a2019?
A) 121 Б) 25 В) 64 Г) 400 Д) 49
29
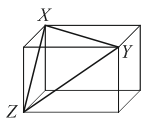
Дан прямоугольный параллелепипед (см. рис.). Стороны треугольника XYZ равны 8 см, 9 см и √55 см. Чему равна диагональ параллелепипеда?
A) √90 см
Б) 10 cм
В) √120 см
Г) 11 cм
Д) 12 cм
30

В клетки квадрата на рисунке вписаны натуральные числа так, что в каждой строчке и в каждом столбце имеется по одному из чисел 1, 2, 3, 4, 5. Кроме того, суммы чисел в трёх частях квадрата, выделенных на рисунке, одинаковы. Если в нижнем левом углу квадрата вписано число 2, то какое число вписано в правом верхнем углу?
A) 1 Б) 2 В) 3 Г) 5 Д) 6