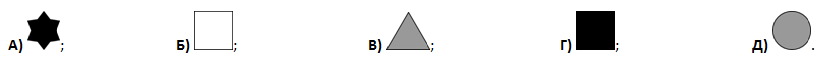1
Чему равна сумма двух последних цифр произведения
1 • 2 • 3 • 4 • 5 • 4 • 3 • 2 • 1?
A) 2 Б) 4 В) 6 Г) 8 Д) 16
2
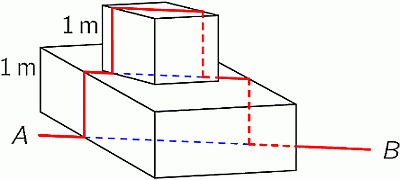
Муравей ходил каждый день по прямой горизонтальной линии от точки А до В, которые находятся на расстоянии 5 м друг от друга. Однажды люди разместили на его пути два блока высотой 1 м каждый (см. рис.). Теперь муравей идёт так, чтобы вертикальной проекцией его пути на поверхность был отрезок АВ. Чему теперь равна длина его пути?
A) 7 м
Б) 9 м
В) 5 + 4√2 м
Г) 9 - 2√2 м
Д) длина зависит от того, под какими углами к направлению пути расположены блоки
3
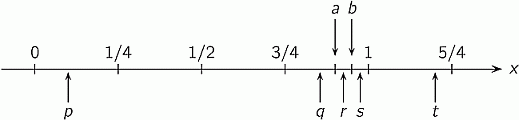
Рене обозначил на числовой прямой две точки a и b. Какое из чисел p, q, r, s, t наиболее точно изображает произведение ab?
A) p Б) q В) r Г) s Д) t
4
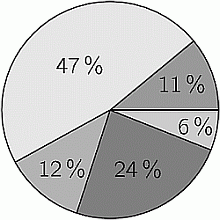
Круговая диаграмма показывает, как ученики добираются в школу. Тех, кто едет на велосипеде, примерно вдвое больше, чем тех, кто едет на общественном транспорте. На автомобиле приезжают примерно столько же, сколько приходят пешком. Остальные пользуются мопедом. Сколько процентов школьников приезжают на мопеде?
A) 6% Б) 11% В) 12% Г) 24% Д) 47%
5

Сумма пяти трёхзначных чисел на рисунке справа равна 2664. Чему равна сумма A + B + C + D + E ?
A) 4 Б) 14 В) 24 Г) 34 Д) 44
6
Чему равно значение выражения 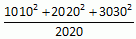 ?
?
A) 22020 Б) 3030 В) 4040 Г) 6060 Д) 7070
7
Пусть a, b, c – натуральные числа, удовлетворяющие условиям 1 ≤ a ≤ b ≤ c и abc = 1000000. Какое наибольшее значение может иметь b?
A) 100 Б) 250 В) 500 Г) 1000 Д) 2000
8
Если D собак весят K килограммов, а E слонов весят столько же, сколько M собак, то сколько килограммов весит один слон?
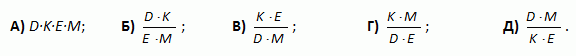
9
Имеется два кубика, у каждого две грани красные, две грани синие и две грани белые. Если бросить оба кубика вместе, то какова вероятность, что на них выпадут одинаковые цвета?
A) 1/12 Б) 1/9 В) 1/6 Г) 2/9 Д) 1/3
10
Какое из следующих выражений не делится на 3 ни при каких целых значениях n?
A) 5n + 1
Б) n2
В) n(n + 1)
Г) 6n - 1
Д) n3 - 2
11
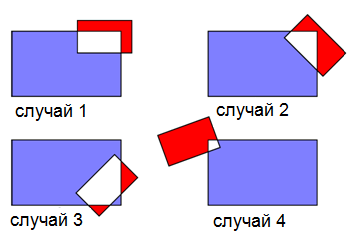
Синий и красный прямоугольники перекрываются. На рисунке показано 4 соответствующих случая. Обозначим через B площадь части синего прямоугольника, которая не является общей для обоих прямоугольников, а через R – площадь части красного прямоугольника, которая не является общей для этих прямоугольников. В каком случае разность B – R наибольшая?
A) в 1-м
Б) во 2-м
В) в 3-м
Г) в 4-м
Д) во всех случаях одинаковая
12
Пять монет лежат на столе «решкой» вверх. За один ход можно перевернуть ровно три монеты. Какое наименьшее количество таких ходов нужно сделать, чтобы все монеты лежали «орлом» вверх?
A) 2 Б) 3 В) 4 Г) 5 Д) это сделать невозможно
13
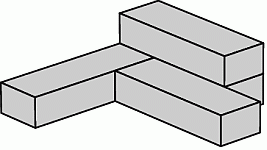
Четыре одинаковых коробки склеили так, что получилась конструкция, изображённая на рисунке. Чтобы целиком окрасить одну такую коробку требуется 1 литр краски. Сколько литров краски нужно, чтобы окрасить полученную конструкцию?
A) 2,5 Б) 3 В) 3,25 Г) 3,5 Д) 4
14
Какое из следующих значений не может принимать выражение
(a - b)2 + (b - c)2 + (c - a)2
ни при каких целых a, b и c?
A) 0 Б) 1 В) 2 Г) 6 Д) 8
15
Две первые цифры 100-значного числа равны 2 и 9 (в указанном порядке). Сколько цифр имеет квадрат этого числа?
A) 101 Б) 199 В) 200 Г) 201 Д) невозможно определить
16
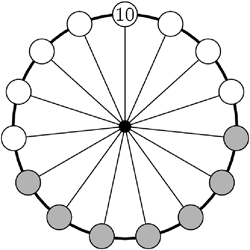
Митя вписал 15 чисел в кружочки на колесе. На рисунке показано только одно из них – число 10. Известно, что сумма чисел в любых семи последовательных кружочках (например, серых на рисунке) одна и та же. Сколько из чисел 75, 216, 365 и 2020 могут быть суммами всех 15-и вписанных чисел?
A) ни одно Б) одно В) два Г) три Д) четыре
17
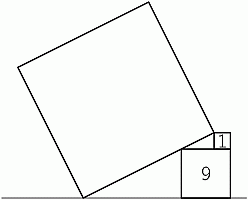
Большой квадрат касается двух меньших квадратов, площади 1 и 9, так, как показано на рисунке. Чему равна площадь большого квадрата?
A) 49 Б) 80 В) 81 Г) 82 Д) 100
18
Последовательность fn задана следующим образом: f1 = 1, f2 = 3 и fn+2 = fn + fn+1 для всех n ≥ 1. Сколько чисел среди первых 2020 членов последовательности являются чётными?
A) 673 Б) 674 В) 1000 Г) 1011 Д) 1347
19
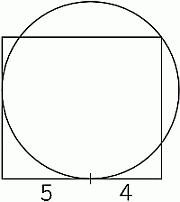
Круг касается двух сторон прямоугольника и проходит через одну из его вершин. Одна из точек касания делит соответствующую сторону на отрезки длиной 5 и 4 (см. рис.). Чему равна площадь данного прямоугольника?
A) 27π Б) 25π В) 72 Г) 63 Д) другой ответ
20
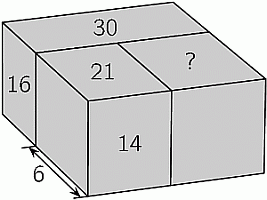
Прямоугольный параллелепипед построен из трёх меньших так, как показано на рисунке. Ширина одного из них равна 6, а площади некоторых их граней равны 14, 21, 16, 30 (см. рис.). Чему равна площадь грани, отмеченной знаком вопроса?
A) 18 Б) 24 В) 28 Г) 30 Д) невозможно определить
21
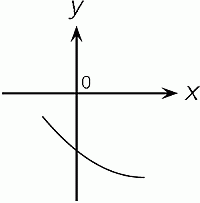
На рисунке показана часть параболы y = ax2 + bx + c . Какое из следующих чисел является положительным?
A) с
Б) b + с
В) ас
Г) bс
Д) аb
22
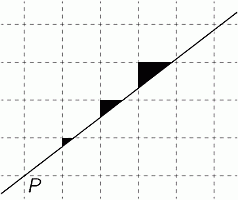
На клетчатой бумаге кенгурёнок рисует линию, проходящую через вершину клетки P, и окрашивает три треугольника, как показано на рисунке. Каким может быть отношение площадей этих треугольников?
A) 1: 2: 3
Б) 1: 2: 4
В) 1: 3: 9
Г) 1: 4: 8
Д) ни одним из указанных в А) – Г)
23
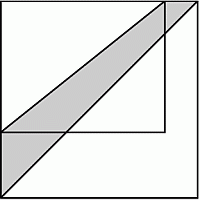
Одну сторону прямоугольника увеличили на 20%, а другую – на 50%. В результате получился квадрат (см. рис.). Площадь серого четырёхугольника равна 30 см2. Чему равна площадь исходного прямоугольника?
A) 60 см2
Б) 65 см2
В) 70 см2
Г) 75 см2
Д) 80 см2
24
Натуральное число N делится на все числа от 2 до 11, кроме каких-то двух из них. Какими могут быть эти два числа?
A) 2 и 3
Б) 4 и 5
В) 6 и 7
Г) 7 и 8
Д) 10 и 11
25
Утром в магазине продавали мороженое 16 разных вкусов. Аня составила себе мороженое с двумя разными вкусами. К вечеру несколько видов мороженого были распроданы. Белла составило себе мороженое с тремя из оставшихся вкусов. Оказалось, что и у Анны и Беллы было одинаковое число способов составить своё мороженое. Сколько видов мороженого было распродано к вечеру?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
26
У Толи в коробке лежит 71 камешек. Ему разрешается вынуть ровно 30 камешков из коробки или вложить в неё ровно 18 камешков. Толя может применять эти операции любое количество раз. Какое наименьшее количество камешков Толя может оставить в коробке?
A) 1 Б) 3 В) 5 Г) 7 Д) 11
27
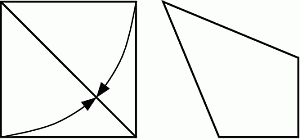
Ваня взял квадратный лист бумаги со стороной 1 и сложил две его стороны к диагонали, как показано на рисунке. Чему равна площадь полученного четырёхугольника?
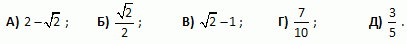
28
Айсберг имеет форму куба. Ровно 90% его объёма скрыто под поверхностью воды. Над поверхностью воды видна только одна вершина и, частично, три ребра этого куба. Длины видимых частей этих рёбер: 24 м, 25 м и 27 м. Чему равна длина всего ребра куба?
A) 30 м Б) 33 м В) 34 м Г) 35 м Д) 39 м
29
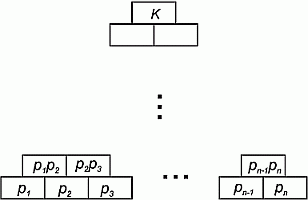
В нижнем ряду пирамиды записано n различных простых чисел, от p1 до pn. Пирамиду заполнили числами так, что над двумя соседними одного ряда всегда записано их произведение. В вершине куба записано число
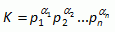
Известно, что α2 = 8. Сколько чисел таблицы делятся на p4?
A) 4 Б) 16 В) 24 Г) 28 Д) 36
30
Адам и Бритт пытаются выяснить, какая из следующих фигур нравится Карлу.

Адам знает, что Карл сообщил Бритту её форму. Бритт знает, что Карл сообщил Адаму её цвет. Затем состоялся следующий разговор. Адам: «Я не знаю, какая фигура нравится Карлу, и я знаю, что Бритт тоже не знает. Бритт: «Сначала, я не знал любимую фигуру Карла, но теперь я её знаю». Адам: «Теперь я тоже её знаю». Какая фигура нравится Карлу?