1
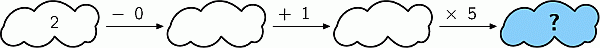
A) 6 Б) 7 В) 8 Г) 10 Д) 15
2
У Эрика есть 10 одинаковых металлических пластин.
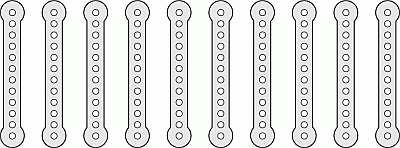
Он свинтил их парами в 5 более длинных пластин (см. рис.). Какая из них самая длинная?
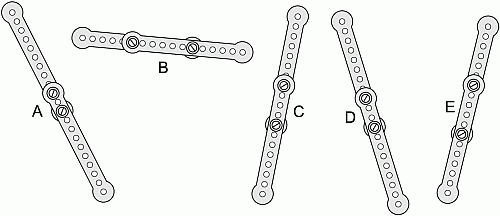
A) A Б) B В) C Г) D Д) E
3
Какое число закрыто квадратом на втором из двух следующих правильных равенств, если известно, что треугольниками закрыты одинаковые числа?
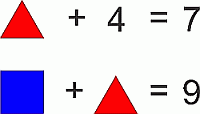
A) 2 Б) 3 В) 4 Г) 5 Д) 6
4
Произведение цифр некоторого двузначного числа равно 15. Чему равна сумма цифр этого числа?
A) 2 Б) 4 В) 6 Г) 8 Д) 10
5
Мы хотим соединить отрезками 9 точек на окружности. Начав c точки 1, будем проводить отрезки к каждой второй точке, пока не вернёмся в точку 1. Первые два отрезка уже нарисованы на рисунке.
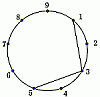
Какую фигуру мы получим, когда процесс будет закончен?

6
У Люси в кошельке было несколько кенго (см. рис.).
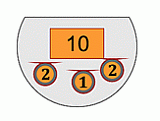
Она зашла в магазин и купила мячик за 7 кенго. Сколько кенго осталось в кошельке у Люси после покупки мячика?

7
На рисунке изображён остров с необычной береговой линией и несколькими лягушками. Сколько из этих лягушек сидит на острове?
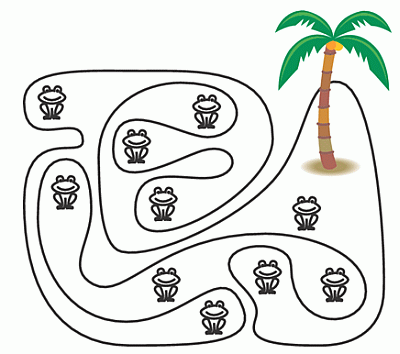
A) 5 Б) 6 В) 7 Г) 8 Д) 9
8
Сверху на зонтике написано слово KANGAROO (см. рис.).
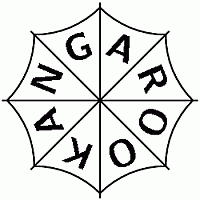
На каком из следующих рисунков изображён вид зонтика сбоку?

9
Вася хочет разрезать бумажную фигуру на рисунке
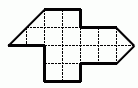
на треугольники вида  . Сколько треугольников у него получится?
. Сколько треугольников у него получится?
A) 8 Б) 12 В) 14 Г) 15 Д) 16
10
У Люси есть 7 яблок и 2 банана. Она дала 2 яблока Юре, который взамен дал ей несколько бананов. В результате у Люси яблок и бананов стало поровну. Сколько бананов дал Юра Люсе?
A) 2 Б) 3 В) 4 Г) 5 Д) 7
11
Толя сложил куб из серых и белых кубиков (см. рис.) так, что никакие два кубика одного цвета не соприкасаются по грани. Сколько белых кубиков Толя использовал?

A) 10 Б) 12 В) 13 Г) 14 Д) 15
12
В конькобежных соревнованиях участвовало 10 спортсменов. Коля опередил на 3 гонщика больше, чем опередили его. Какое место занял Коля?
A) 1 Б) 3 В) 4 Г) 6 Д) 7
13
У Иосифа есть 4 игрушки: автомобиль, самолёт, мяч и корабль. Он хочет расставить их в ряд на полке так, чтобы рядом с автомобилем стояли корабль и самолёт. Сколько существует способов так расставить игрушки?
A) 2 Б) 4 В) 5 Г) 6 Д) 8
14
Петя едет на велосипеде по дорожкам в парке (см. рис.). Он стартует из пункта S в направлении стрелки. На первом перекрёстке Петя поворачивает направо, затем налево, потом снова направо, затем налево, и т. д. Какой из пунктов он не сможет проехать ни разу?
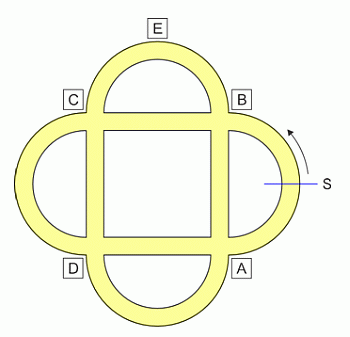
A) A Б) B В) C Г) D Д) E
15

На рисунке – 5 божьих коровок. Две божьи коровки дружат между собой, если количества пятен у них на крыльях отличаются ровно на 1. В день проведения конкурса «Кенгуру» каждая из божьих коровок отправила одно приветственное SMS каждой своей подружке. Сколько поздравительных SMS было отправлено?
A) 2 Б) 4 В) 6 Г) 8 Д) 9
16

Фигуру на рисунке разрезали на 3 одинаковые части. Как может выглядеть одна такая часть?

17
Лиза вырезала из бумаги фигуру (см. рис.) и хочет свернуть её так, чтобы получился куб. Но по ошибке одна клетка у этой фигуры оказалась лишняя. Какую клетку из этой фигуры нужно вырезать, чтобы фигура не распалась на части, и чтобы после этого её можно было бы свернуть в куб?
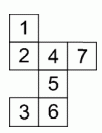
A) 1 Б) 2 В) 3 Г) 6 Д) 7
18
Имеются три квадратные пластины со светлыми прозрачными и чёрными непрозрачными клетками (см. рис.). Какое наибольшее число чёрных клеток можно будет увидеть, если наложить эти квадраты друг на друга так, чтобы их вершины совпали, и посмотреть на них сверху? (Квадраты можно поворачивать, но не переворачивать.)

A) 5 Б) 6 В) 7 Г) 8 Д) 9
19
В пять клеток креста нужно вписать числа 2, 3, 5, 6 и 7 (каждое по одному разу) так, чтобы сумма трёх чисел в столбце равнялась сумме трёх чисел в строке. Какое число нужно вписать в центральную клетку?

A) только 3
Б) только 5
В) только 7
Г) 5 или 7
Д) 3, 5 или 7
20

У Пети есть десять шариков, пронумерованных числами от 0 до 9. Он раздал их трём своим друзьям: 3 шарика – Диме, 4 – Жене и 3 – Ане. После этого друзья Пети вычислили произведения чисел на полученных ими шариках. У Димы получилось 0, у Жени – 72, а у Ани – 90. Чему равна сумма чисел на шариках, которые получил Дима?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
21
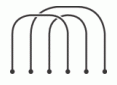
На рисунке показаны три верёвки. С какими из следующих трёх верёвок их нужно связать, совместив концы в том же порядке, как они изображены на рисунках, чтобы получилась одна замкнутая верёвка?

22
На клетчатой бумаге отмечено 16 точек так, как показано на рисунке. Сколько всего существует не равных квадратов с вершинами в отмеченных точках?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
23
Том нарисовал кабана, акулу и носорога и разрезал каждого из них на три части так, как показано на рисунке. Сколько различных (реальных и нереальных) животных можно получить, если из всех этих частей выбрать одну переднюю, одну среднюю и одну заднюю часть и склеить их соответствующим образом?

A) 3 Б) 9 В) 15 Г) 27 Д) 30
24
Аня, Берта, Чарли, Дэвид и Лиза пекли печенье в субботу и воскресенье. За два дня Аня испекла 24 печенья, Берта – 25, Чарли – 26, Дэвид – 27, а Лиза – 28. При этом, кто-то из них в течение двух дней испек в 2 раза больше печенья, чем в субботу, кто-то – в 3 раза больше, чем в субботу, кто-то – в 4 раза, кто-то – в 5 раз, а кто-то – в 6 раз. Кто из этих детей испёк больше всего печенья в субботу?
A) Аня Б) Берта В) Чарли Г) Дэвид Д) Лиза