1
Аня, Боря, Ваня, Галя и Дима подбросили по два игральных кубика. Их результаты показаны на рисунке. Кто выиграл, набрав больше всего очков?

A) Аня Б) Боря В) Ваня Г) Галя Д) Дима
2
Маленькому кенгурёнку 7 недель и 2 дня отроду. Через сколько дней ему исполнится 8 недель?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
3
Какое число следует вписать в клетку со знаком «?» на схеме?
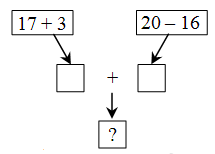
A) 24 Б) 28 В) 36 Г) 56 Д) 80
4

Что увидит клоун Пипо (см. рис.), если посмотрит на себя в зеркало?
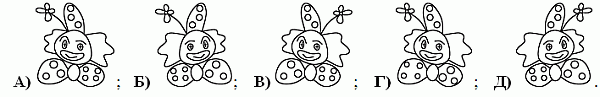
5
Женя с папой пришли в цирк. На входе висит указатель (см. рис.).
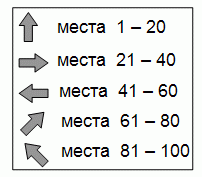
У Жени и папы билеты на места 71 и 72. В каком направлении им следует идти?
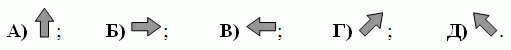
6
Аня поделилась яблоками со своими 5 подругами. Ей и её подругам досталось по половине яблока каждой. Сколько яблок было у Ани?
A) 2 с половиной Б) 3 В) 4 Г) 5 Д) 6
7
Какой фигурой является часть чёрного квадрата, которая накрыта серым прямоугольником (см. рис.)?

A) треугольником Б) квадратом В) пятиугольником Г) кругом Д) прямоугольником
8
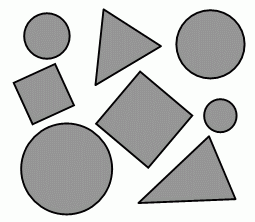
Какое из следующих высказываний о рисунке является верным?
A) кругов и квадратов поровну
Б) кругов меньше, чем треугольников
В) кругов в 2 раза больше, чем треугольников
Г) квадратов больше, чем треугольников
Д) треугольников на 2 больше, чем кругов
9
Сумма цифр года 2016 равна 9. Через какое наименьшее число лет сумма цифр года будет также равна 9?
A) 8 Б) 9 В) 10 Г) 18 Д) 90
10
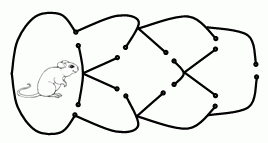
Мышь хочет выбраться из лабиринта. Сколько способов у неё есть, чтобы это сделать, не пролезая ни через одну щель более одного раза?
A) 2 Б) 4 В) 5 Г) 6 Д) 8
11

У Зои есть две карточки. На каждой стороне карточек записано по одному числу. Сумма чисел на одной карточке равна сумме чисел на другой карточке, а сумма всех четырёх чисел на карточках равна 32. На лицевых сторонах карточек записаны числа 5 и 12 (см. рис.). Какие числа записаны на оборотных сторонах карточек?
A) 7 и 0
Б) 8 и 11
В) 11 и 4
Г) 9 и 2
Д) 6 и 3
12
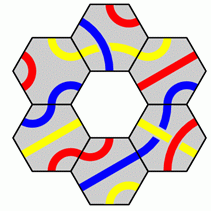
Какую плитку нужно вложить в центр на рисунке, чтобы все линии на ней соединились с такими же линиями на соседних плитках?

13
У каждого из пятерых детей есть по 3 карточки: квадрат, круг и треугольник. Каждый ребёнок положил свои карточки друг на друга, как показано на рисунке. Сколько детей положили треугольник выше квадрата?

A) 1 Б) 2 В) 3 Г) 4 Д) 5
14
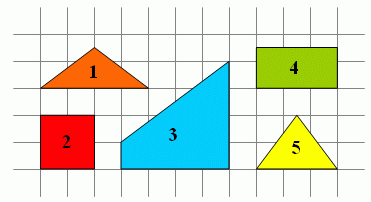
Какие из следующих плиток можно сложить так, чтобы получился квадрат?
A) 1, 3 и 5
Б) 1, 2 и 5
В) 1, 4 и 5
Г) 3, 4 и 5
Д) 2, 3 и 5
15
Лёня решил вписать в каждую клетку таблицы (см. рис.) одно из чисел 1, 2 или 3 так, чтобы в каждой строчке и в каждом столбце было по одному из этих чисел. Два числа он уже вписал так, как показано на рисунке. Чему будет равна сумма чисел в двух серых клетках?

A) 2 Б) 3 В) 4 Г) 5 Д) 6
16
Женя положил 8 монет в какие-то 8 подряд идущих клеток из 11 клеток на рисунке. Сколько всего существует клеток, в которых наверняка находится монета?
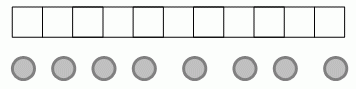
A) 1 Б) 3 В) 4 Г) 5 Д) 6
17
Карточка лежит на столе рисунком вниз. Перевернув её через правую сторону, мы увидим то, что показано на рисунке. Что мы увидели бы, если бы перевернули эту же карточку через верхнюю сторону?
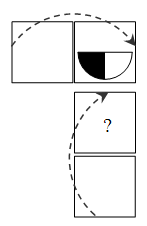

18
Тим, Том и Джим – тройняшки (родились в один день). Их брат Пол старше братьев на 3 года. Какое из следующих чисел может быть суммой возрастов этих четырёх братьев?
A) 25 Б) 27 В) 29 Г) 30 Д) 60
19
При проведении конкурса этот вопрос не оценивался или правильными являются два варианта ответа.
Поэтому при тестовом выполнении он пропускается. При проверке своих ответов вы сможете посмотреть и пропущенный вопрос.
20
У моих собак число ног на 18 больше, чем число носов. Сколько у меня собак?
A) 4 Б) 15 В) 6 Г) 18 Д) 19
21
Катя взвесила пять наборов предметов и четыре из них разместила в порядке возрастания веса слева направо: Q, R, S, T (см. рис.). Между какими наборами
ей следует разместить набор Z, чтобы этот порядок сохранился?
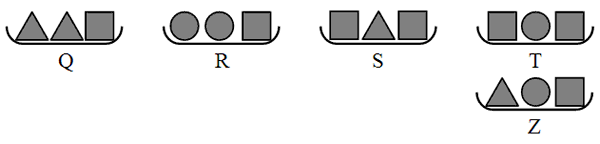
A) слева от Q
Б) между Q и R
В) между R и S
Г) между S и T
Д) правее T
22
Рая сложила 7 чисел и получила сумму 2016. Затем одно из них – число 201 – она заменила числом 102 и снова сложила все числа. Какой результат она получила?
A) 1815 Б) 1914 В) 1917 Г) 2115 Д) 2118
23

Конструкция на рисунке состоит из 27 брусков Lego. Миша разбивает её на две меньших конструкции так, чтобы в одной было в 2 раза больше брусков, чем в другой. Затем он выбирает любую из имеющихся конструкций и делит её на две меньшие части по такому же правилу (пока это возможно). Какую из следующих конструкций он не сможет получить, продолжая этот процесс?
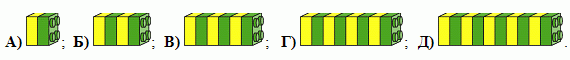
24

Пять воробьёв сидят на проводе так, как показано на рисунке. Некоторые из них смотрят налево, остальные – направо. Каждый воробей чирикнул один раз каждому из воробьёв, сидящих на той стороне, куда он смотрит. Например, Грегор чирикнул 3 раза. Затем один из воробьёв повернулся и стал смотреть в противоположную сторону. После этого снова каждый воробей чирикнул один раз каждому из воробьёв, сидящих на той стороне, куда он смотрит. Во второй раз чириканьев оказалось больше, чем в первый раз. Какой из воробьёв повернулся?
A) Алекс Б) Барт В) Винни Г) Грегор Д) Дэвид