1
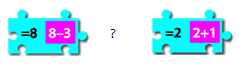
Какую из следующих карточек пазла нужно разместить между карточками на рис. выше, чтобы получились два правильных равенства?
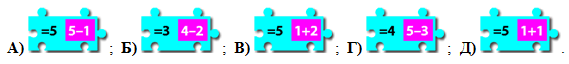
2

Глядя из своего окна, Женя может видеть половину из всех кенгуру в зоопарке (см. рис.). Сколько всего кенгуру в зоопарке?
A) 12 Б) 14 В) 16 Г) 18 Д) 20
3

Двумя стеклянными квадратами, у которых белые клетки прозрачны, а чёрные – нет, накрыли квадрат, изображённый между ними. Какой рисунок будет виден?
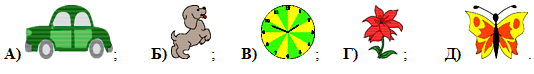
4
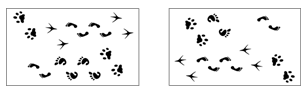
Рисунок с изображением следов перевернули через правую сторону, а потом через нижнюю. Какие следы исчезли?
5

Какое число закрывает панда?
A) 16 Б) 18 В) 20 Г) 24 Д) 28
6
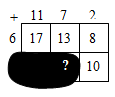
На рисунке показан фрагмент таблицы сложения. Его часть скрывает чернильное пятно. Какое число должно быть в клетке со знаком «?»?
A) 10 Б) 11 В) 12 Г) 13 Д) 15
7
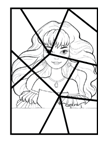
Даша нечаянно разбила зеркало, и оно раскололось на несколько кусков. Сколько из этих кусков являются четырёхугольными, т.е. имеют ровно четыре стороны?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
8
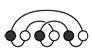
На рисунке показано ожерелье с 6 бусинками. Как оно может выглядеть, если его развернуть?
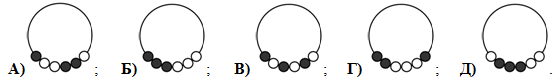
9

На рисунке изображён вид спереди дома, в котором живёт Аня. На обратной стороне её дома есть 3 окна, и нет ни одной двери. Какой вид может иметь обратная сторона Аниного дома?

10
Дано: 
Какое из следующих равенств верно?
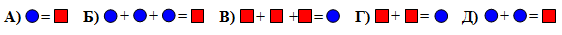
11
Мария покупает шары в пакетах по 5, 10 и 25 штук. Какое наименьшее число пакетов ей нужно купить, чтобы в них было ровно 70 шаров?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
12

Вася сложил лист бумаги в несколько слоёв и проколол сложенный лист ровно один раз. Затем он развернул лист и увидел, что получилось 4 дырки (см. рис. выше). Каким из следующих способов был сложен этот лист?

13
Для участия в турнире по минифутболу сначала записалось 13 детей, а потом ещё 19. Какого наименьшего числа детей ещё не хватает, чтобы всех участников турнира можно было разбить на 6 команд с одинаковым количеством детей в каждой команде?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
14
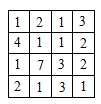
В клетки таблицы 4 × 4 вписаны числа так, как показано на рисунке. Мария нашла в этой таблице квадрат 2 × 2, сумма четырёх чисел которого является наибольшей. Чему равна эта сумма?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
15
Даша хочет приготовить 5 блюд на плите с двумя горелками. На их приготовление требуется 40, 15, 35, 10 и 45 минут. Каждое блюдо может готовиться на любой горелке, но должно полностью готовиться только на одной из них. За какое наименьшее время Даша может приготовить все блюда?
A) 60 минут
Б) 70 минут
В) 75 минут
Г) 80 минут
Д) 85 минут
16
Какое число нужно вписать в кружок, отмеченный знаком «?» на рисунке?
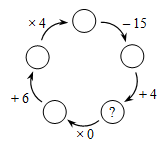
A) 10 Б) 11 В) 12 Г) 13 Д) 14
17
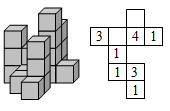
На рисунке показана конфигурация из кубиков, и справа от неё изображён план этой конфигурации. Чему должна быть равна сумма чисел в пустых клетках на плане?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
18
Какова длина поезда на рисунке?

A) 55 м Б) 115 м В) 170 м Г) 220 м Д) 230 м
19
Женя ездит в школу на автобусе. До остановки автобуса ему идти 5 минут. Автобусы ходят через каждые 10 минут. В автобусе до школы Жене ехать 15 минут. От автобусной остановки до школы ему идти 5 минут. Занятия в школе начинаются в 8:00. В какое самое позднее время Женя может выйти из дома, чтобы наверняка успеть к началу занятий?
A) 7:15 Б) 7:25 В) 7:30 Г) 7:35 Д) 7:40
20
В зверинце есть жираф, слон, лев и черепаха. Сюзанна хочет посетить ровно двух из этих животных. Но первым не должен быть лев. Сколько всего таких различных посещений зверинца она может осуществить?
A) 3 Б) 7 В) 8 Г) 9 Д) 12
21
Четыре брата съели 11 пирожных. Каждый из них съел не менее одного пирожного, никакие двое не съели одинакового количества пирожных. Трое из братьев съели вместе 9 пирожных, а один из них съел 3 пирожных. Сколько пирожных съел тот брат, который съел их больше всего?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
22
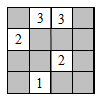
В некоторых клетках таблицы справа Зоя нарисовала по одному смайлику ☺. Затем в некоторых пустых клетках она записала число смайликов в соседних (по стороне или по вершине) клетках. Все эти числа указаны в таблице. Сколько смайликов нарисовала Зоя?
A) 4 Б) 5 В) 7 Г) 8 Д) 11
23
В десяти коробках находятся различные количества конфет: от 1 до 10. Пятеро мальчиков взяли по две коробки. Андрею досталось 5 конфет, Васе – 7, Вадиму – 9, Грише – 15. Сколько конфет досталось пятому мальчику, Диме?
A) 9 Б) 11 В) 13 Г) 17 Д) 19
24

У Кати четыре ромашки: с 6, 7, 8 и 11 лепестками. Катя выбирает какие-то три из этих цветков и отрывает у них по одному лепестку. Затем она снова выбирает какие-то три из этих цветков и отрывает у них по одному лепестку. Катя повторяет такие действия до тех пор, пока это возможно. Какое наименьшее число лепестков может остаться в конце, когда очередного действия нельзя будет выполнить?
A) 1 Б) 2 В) 3 Г) 4 Д) 5