1
Гриб растёт непрерывно. Маша фотографировала его каждый день с понедельника по пятницу. Какой из следующих снимков она сделала во вторник?

2

Какая из следующих плиток дополняет узор на рисунке?

3

Тима решил закрасить все клетки, в которых значение записанного выражения равно 20. Что у него должно получиться?

4
У какой из следующих фигур окрашенная часть имеет наибольшую площадь?

5
У Коли есть фигурки, изображённые на рисунке. Какую из следующих композиций он может составить из этих фигурок?
6
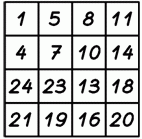
Кенгуру прыгает по клеткам квадрата, начиная с числа 1. Каждый следующий прыжок приходится на клетку с числом, большим на 3. До какого наибольшего числа Кенгуру сможет допрыгать?
A) 11 Б) 14 В) 18 Г) 19 Д) 24
7

Жора наклеил шесть стикеров на грани кубика. На рисунке показан вид кубика с двух сторон. Какой стикер находится на грани, противоположной грани с уткой?

8

Лена хочет разрезать полоску на рисунке по сторонам клеток так, чтобы все части были разной длины. Какое наибольшее число частей у неё может получиться?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
9
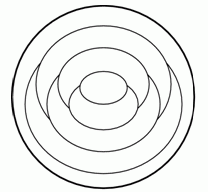
Света окрашивает каждую часть круга на рисунке в красный, синий или жёлтый цвет. Части, имеющие общую границу, она красит в разные цвета. Внешнюю часть Света окрасила в красный цвет. Сколько всего частей она окрасит в красный цвет?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
10
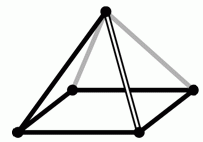
Леся смотрит на пирамиду сверху. Что она видит?

11
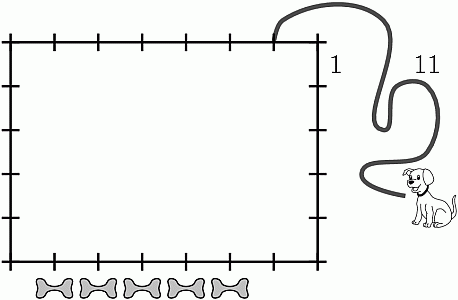
Денис привязал собаку на поводок длиной 11 метров на расстоянии 1 метр от угла сарая 7 × 5 метров. Возле сарая лежат 5 косточек, как показано на рисунке. До скольких из них собака может добраться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
12
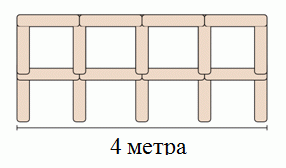
Лёня строит забор из столбов длины 1 метр. На рисунке показан его фрагмент забора длиной 4 метра. Сколько всего столбов нужно Лёне, чтобы построить 10-метровый забор?
A) 22 Б) 30 В) 33 Г) 40 Д) 42
13
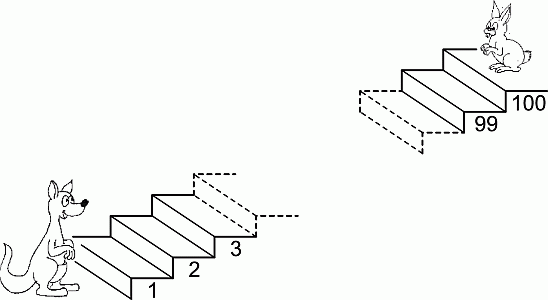
Каждый раз, когда Кенгуру прыгает на 7 ступенек вверх, Кролик прыгает на 3 ступеньки вниз. На какой ступеньке они встретятся?
A) 53 Б) 60 В) 63 Г) 70 Д) 73
14
Карина задумала три числа. Их сумма равна 50. Из каждого задуманного числа Карина вычла некоторое секретное число. В результате она получила 24, 13 и 7. Какое из следующих чисел является одним из задуманных чисел?
A) 9 Б) 11 В) 13 Г) 17 Д) 23
15
Амалия хочет построить корону из 10 одинаковых пятиугольников вида
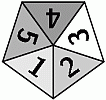 .
.
Они должны соприкасаться сторонами треугольников с одинаковыми числами. Какое число окажется в треугольнике, отмеченном знаком X?
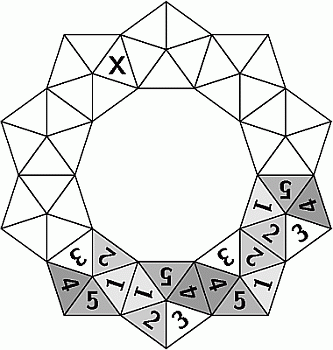
A) 1 Б) 2 В) 3 Г) 4 Д) 5
16
У Феди есть два вида палочек: короткие длиной 1 см и длинные длиной 3 см. Из какого из следующих наборов палочек Федя может сложить квадрат, если палочки нельзя ломать и накладывать друг на друга?
A) 5 коротких, 2 длинных
Б) 3 коротких, 3 длинных
В) 4 коротких, 2 длинных
Г) 6 коротких
Д) 6 длинных
17
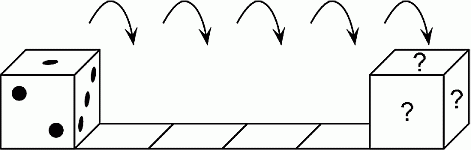
У стандартного кубика сумма точек на противоположных гранях равна 7. Кубик лежит так, как показано на рисунке. Чему будет равна сумма точек на гранях, отмеченных знаком «?» после пяти перекатываний вправо?
A) 6 Б) 7 В) 9 Г) 11 Д) 12
18
Шестеро школьников заказали по одному шарику мороженого: 3 ванильного, 2 шоколадного и 1 лимонного. Они добавили к мороженым 3 вишни, 2 вафли и 1 дольку мандарина, к каждому мороженому что-то одно. При этом одинаковых сочетаний не получилось. Какое из следующих сочетаний не могло получиться?
A) шоколадное с вишней
Б) ванильное с вишней
В) лимонное с вафлей
Г) шоколадное с вафлей
Д) ванильное с мандарином
19
У людей некоторых народов бывает несколько имен. Один из братьев Гримм решил узнать, как зовут невесту его брата. Он задал ей 3 вопроса: "Вас зовут Адель Лилли Клео?", "Вас зовут Адель Лаура Кора?", "Вас зовут Эбби Лора Клео?" Каждый раз ровно одно имя было верным и стояло на нужном месте. Как зовут невесту брата?
A) Эбби Лили Кора
Б) Эбби Лаура Кора
В) Адель Лаура Клео
Г) Адель Лили Кора
Д) Эбби Лаура Клео
20
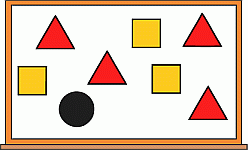
Учитель написал все числа от 1 до 8 на доске. Затем он закрыл их треугольниками, квадратами и кружочком. Сумма всех чисел, закрытых треугольниками, равна 10, а сумма всех чисел, закрытых квадратами, равна 20. Какое число закрыто кружком?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
21

У Жени есть несколько одинаковых рисунков попугаев. Она хочет раскрасить голову, хвост и крылья каждого попугая в красный, синий и зелёный цвета так, чтобы все три цвета присутствовали на каждом рисунке. Она окрасила голову одного попугая в красный цвет, крылья – в зелёный, а хвост – в синий. Сколько ещё попугаев она может раскрасить так, чтобы все попугаи были окрашены по-разному?
A) 1 Б) 2 В) 4 Г) 5 Д) 8
22
В летний лагерь «Кенгуру» съехались 43 школьника из нескольких стран, по 5 или 6 человек из каждой страны. Сколько стран прислали школьников в этот лагерь?
A) 4 Б) 6 В) 7 Г) 8 Д) 9
23
Какую из следующих фигур нельзя разрезать на три различные связные части с одинаковым количеством клеток? Разрезы можно делать только по сторонам клеток.
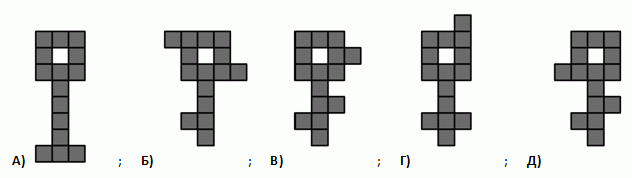
24
Какое наибольшее значение может иметь выражение
KAN + GA – ROO,
если в нём буквы заменить ненулевыми цифрами (одинаковые буквы – одинаковыми цифрами, а разные – разными).
A) 925 Б) 933 В) 939 Г) 942 Д) 948