1
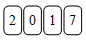
В ряд лежат 4 карты (см. рис.). Какой ряд из этих карт нельзя получить, поменяв местами только две из карт?
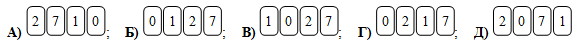
2
У мухи 6 ног, а у паука 8 ног. Вместе у 3 мух и 2 пауков столько же ног, сколько ног у 9 цыплят и …
A) 2 котят
Б) 3 котят
В) 4 котят
Г) 5 котят
Д) 6 котят
3
У Алисы есть 4 плитки вида 
. Какую из следующих фигур Алиса не сможет сложить из этих плиток?
4
Коля знает, что 1111 × 1111 = 1234321. Чему равно произведение 1111 × 2222 ?
A) 3456543
Б) 2345432
В) 2234322
Г) 2468642
Д) 4321234
5
На некоторой планете 10 островов соединены 12 мостами так, как показано на рисунке. Какое наименьшее число мостов нужно закрыть, чтобы нельзя было добраться по мостам от острова A до острова B?
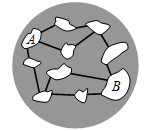
A) 1 Б) 2 В) 3 Г) 4 Д) 5
6
Носороги Джейн, Кейт и Линн вышли на прогулку. Джейн идёт впереди, а Линн – позади. Джейн весит на 500 кг больше, чем Кейт. Кейт весит на 1000 кг меньше, чем Линн. На каком из следующих рисунков показано правильное расположение носорогов на прогулке?
7
На каждой грани специального кубика записано некоторое число. Суммы чисел у пар противоположных граней равны. На пяти из граней записаны числа 5, 6, 9, 11 и 14. Какое число записано на шестой грани?
A) 4 Б) 7 В) 8 Г) 13 Д) 15
8
Мартин хочет окрасить клетки таблицы на рисунке так, чтобы треть клеток были синими, половина – жёлтыми, а остальные красными. Сколько клеток должны быть красными?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
9
Пока Петя решает 2 задачи на конкурсе «Кенгуру», Вася успевает решить 3 задачи. Всего вдвоём они решили 30 задач. На сколько задач Вася решил больше, чем Петя?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
10
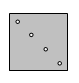
Боря сложил лист бумаги и проколол его ровно один раз. Когда он развернул лист, то увидел 4 дырки (см. рис.). На каком из следующих рисунков показано, как Боря складывал лист?
11
В мебельном магазине продаются диваны, двухместные кресла и обычные кресла. Все они изготовлены из одинаковых модульных частей, как показано на рисунке. Ширина дивана (включая подлокотники) равна 220 см, а двухместного кресла – 160 см. Чему равна ширина кресла?
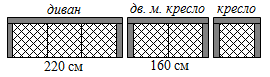
A) 60 см Б) 80 см В) 90 см Г) 100 см Д) 120 см
12
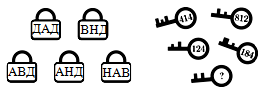
5 ключей на рисунке подходят к 5 замкам. Буквами на замках зашифрованы цифры на ключах (одинаковые цифры – одинаковыми буквами, а разные – разными). Что должно быть написано на последнем ключе?
A) 382 Б) 282 В) 284 Г) 823 Д) 824
13
Толя записал 31-значное число 1234567891011121314151617181920. Какое наибольшее число он может получить, если сотрёт какие-то 24 из цифр данного числа?
A) 9671819 Б) 9567892 В) 9781920 Г) 9912345 Д) 9818192
14
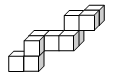
Миша хочет поместить конструкцию, изображённую на рисунке, в обычную коробку. Какие наименьшие размеры могут быть у такой коробки?
A) 3 × 3 × 4
Б) 3 × 5 × 5
В) 3 × 4 × 5
Г) 4 × 4 × 4
Д) 4 × 4 × 5
15
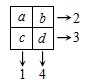
Если сложить числа в строчках и столбцах таблицы 2 × 2, то получатся результаты, показанные на рисунке. Какое из следующих утверждений верно?
A) a равно d
Б) d равно c
В) a больше, чем d
Г) a меньше, чем d
Д) c больше, чем b
16
Петя путешествовал пешком в горах в течение 5 дней: с понедельника по пятницу. Каждый день он проходил на 2 км больше, чем в предыдущий день. Всего за 5 дней Петя прошёл расстояние, равное 70 км. Сколько километров он прошёл в четверг?
A) 12 Б) 13 В) 14 Г) 15 Д) 16
17
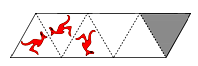
В трёх треугольниках на рисунке изображены кенгуру. Штриховые линии отражают рисунки, как зеркала. Как будет расположен рисунок кенгуру в последнем (сером) треугольнике?
18
У Бори есть некоторая сумма денег и три волшебные палочки, каждой из которых он обязан воспользоваться ровно один раз. Первая палочка увеличивает сумму денег на 2 рубля, вторая уменьшает на 2 рубля, а третья увеличивает в 2 раза. В каком порядке Боря должен использовать эти палочки, чтобы получить наибольшую возможную сумму денег?
A) «× 2», «+ 2», «– 2»
Б) «+ 2», «– 2», «× 2»
В) «× 2», «– 2», «+ 2»
Г) «+ 2», «× 2», «– 2»
Д) «– 2», «+ 2», «× 2»
19
Рома нарисовал 3 квадрата со сторонами 2 см, 4 см и 6 см. Вершина второго квадрата находится в центре первого квадрата, а вершина третьего квадрата – в центре второго, как показано на рисунке. Чему равна площадь полученной фигуры?
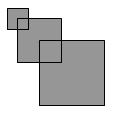
A) 56 см 2
Б) 51 см 2
В) 52 см 2
Г) 48 см 2
Д) 36 см 2
20
Четыре гандболиста забили в матче разные количества голов. Из них Майк забил наименьшее число голов, а остальные трое гандболистов забили вместе 20 голов. Какое наибольшее число голов мог забить Майк?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
21
Брусок 
склеен из двух серых и одного белого кубиков. Какой из следующих кубов можно построить из 9 таких брусков?
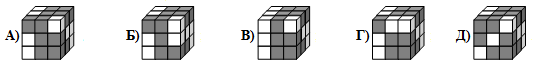
22
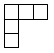
Числа 1, 2, 3, 4, и 5 нужно вписать в клетки фигуры на рисунке так, чтобы выполнялись условия:
1) если одно число ниже другого, то оно больше,
2) если одно число правее другого, то оно тоже больше.
Сколько существует различных способов так вписать данные числа?
A) 3 Б) 4 В) 5 Г) 6 Д) 8
23
8 кенгуру стоят в ряд так, как показано на рисунке. В какой-то момент два соседних кенгуру, которые смотрят друг на друга, перепрыгивают друг через друга. Затем снова два соседних кенгуру, которые смотрят друг на друга, перепрыгивают друг через друга и т.д. Какое число таких перепрыгиваний может быть сделано до того, как они станут невозможны?
A) 2 Б) 10 В) 12 Г) 13 Д) 16
24
Моника выбрала какие-то 5 различных чисел. Затем некоторые из них она умножила на 2, а остальные – на 3 так, чтобы получилось наименьшее количество различных результатов. Какое наименьшее количество различных результатов могло у неё получиться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
25
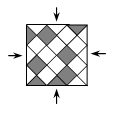
Квадратный пол на рисунке покрыт треугольными и квадратными плитками серого и белого цвета. Какое наименьшее число серых плиток нужно переместить, чтобы узор на полу выглядел одинаково со всех четырёх сторон?
A) 3 треуг. и 1 квадр.
Б) 1 треуг. и 3 квадр.
В) 1 треуг. и 1 квадр.
Г) 3 треуг. и 3 квадр.
Д) 3 треуг. и 2 квадр.
26
В коробке находятся только красные и зелёные шары. Среди любых 5 шаров есть, по крайней мере, 1 красный. А среди любых 6 шаров есть, по крайней мере, 1 зелёный. Какое наибольшее число шаров может быть в этой коробке?
A) 11 Б) 10 В) 9 Г) 4 Д) 5
27
В коробке находятся 8 карточек, на каждой карточке записано одно число. Алле нравятся чётные числа, Вале – числа, кратные 3, а Гале – числа, кратные 5. Названные девочки по очереди заглядывают в коробку и вытаскивают все карточки с любимыми числами. Алла вытащила карточки с числами 32 и 52, Валя – с числами 24, 33 и 45, а Галя – с числами 20, 25 и 35. В каком порядке девочки вытаскивали карточки?
A) Алла, Галя, Валя
Б) Галя, Валя, Алла
В) Валя, Алла, Галя
Г) Валя, Галя, Алла
Д) Галя, Алла, Валя
28
Женя хочет вписать по одному натуральному числу в каждую ячейку диаграммы (см. рис.) так, чтобы каждое число, расположенное выше нижнего ряда, являлось суммой двух чисел в соседних ячейках, расположенных непосредственно снизу от него. Какое наибольшее количество нечётных чисел может вписать Женя?
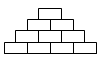
A) 4 Б) 5 В) 6 Г) 7 Д) 8
29
У Юли есть четыре различных цветных карандаша. Она хочет раскрасить карту острова, разделённого на четыре страны (см. рис.), так, чтобы страны с общей границей были окрашены в разные цвета. Сколько таких различных раскрасок существует?
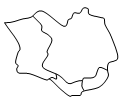
A) 12 Б) 18 В) 24 Г) 36 Д) 48
30
На каждой клетке доски 6 × 6 стоит лампа. В исходном положении некоторые лампы включены. Через каждую минуту включается всякая невключённая лампа, если не менее чем в двух соседних с ней по стороне клетках лампы включены. Какое наименьшее число ламп должно быть включено вначале, чтобы через некоторое время все лампы могли стать включёнными?
A) 4 Б) 5 В) 6 Г) 7 Д) 7