1

Катя начала рисовать кота (см. рис.). Как может выглядеть рисунок, когда он будет завершён?

2
У народа майя запись чисел состояла из точек и полосок. Точка означала число 1, а полоска – число 5. Как у майя выглядела запись числа 17?
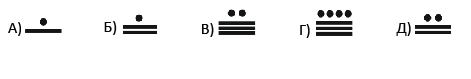
3
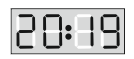
Электронные часы показывают время 20:19 (см. рис.). Что они будут показывать через кратчайшее время после этого при условии, что на циферблате будут те же цифры?
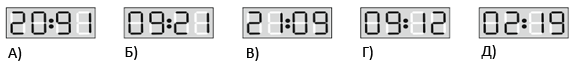
4
В детском саду 14 девочек и 12 мальчиков. Половина детей пошла на прогулку. Какое наименьшее число девочек может быть среди них?
A) 5 Б) 4 В) 3 Г) 2 Д) 1
5
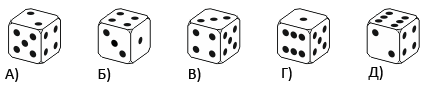
Сумма количеств точек на противоположных гранях стандартного игрального кубика равна 7. Какой из следующих кубиков может являться стандартным?
6
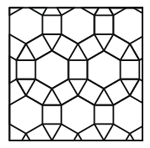
Какой из следующих геометрических фигур нет в узоре?

7

Лариса хочет окрасить в чёрный цвет квадрат 2×2 на рисунке. Сколькими способами она может его выбрать?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
8
На гранях кубика записаны шесть различных наименьших натуральных нечётных чисел. Толя три раза подбросил кубик. Какое из следующих чисел не может быть суммой выпавших чисел?
A) 21 Б) 3 В) 20 Г) 19 Д) 29
9
Сумма возрастов группы кенгуру равна 36 лет. Через два года сумма их возрастов будет равна 60 лет. Сколько кенгуру в этой группе?
A) 10 Б) 12 В) 15 Г) 20 Д) 24
10
Миша окрашивает поверхности следующих фигур, построенных из одинаковых кубиков. В основании всех фигур находится 8 кубиков. На окраску какой из фигур понадобится больше всего краски?

11
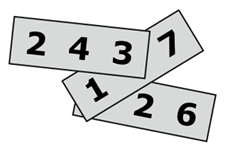
На каждой из трёх полосок бумаги написано трёхзначное число (см. рис.). Сумма этих трёх чисел равна 826. Две цифры скрыты. Чему равна их сумма?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
12

Лягушка Квака обычно съедает 5 пауков в день. Но когда Квака очень голодна, она съедает 10 пауков в день. Квака съела 60 пауков за 9 дней. Сколько из этих дней она была очень голодна?
A) 1 Б) 2 В) 3 Г) 6 Д) 9
13
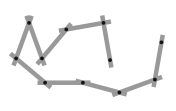
Павел играет с линейкой, состоящей из 10 одинаковых вращающихся относительно друг друга частей (см. рис.). Какую из следующих фигур он не может сложить из такой линейки?

14
Пять одинаковых квадратов разбили на клетки и окрасили в шахматном порядке так, как показано ниже. У какого из этих квадратов площадь чёрной части наибольшая?

15
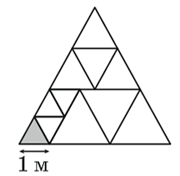
Большой равносторонний треугольник разбит на меньшие равносторонние треугольники так, как показано на рисунке. Чему равен периметр большого треугольника?
A) 15 м Б) 17 м В) 18 м Г) 20 м Д) 21 м
16
В саду ведьмы было 30 животных: собаки, кошки и мыши. Ведьма превратила 6 собак в кошек. Затем она превратила 5 кошек в мышей. В результате собак, кошек и мышей стало поровну. Сколько кошек было вначале?
A) 4 Б) 5 В) 9 Г) 10 Д) 11
17
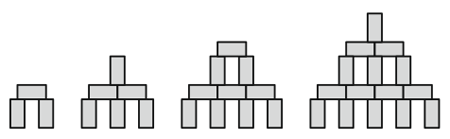
Из блоков 1см×1см×2см можно строить башни, как показано на рисунке. Какой высоты будет башня, построенная таким способом из 28 блоков?
A) 9 см Б) 11 см В) 12 см Г) 14 см Д) 17 см
18
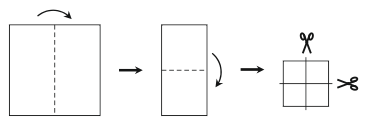
Вера дважды сложила квадратный лист бумаги, а затем разрезала его дважды так, как показано на рисунке. Сколько кусков бумаги в результате получилось?
A) 6 Б) 8 В) 9 Г) 12 Д) 16
19
Алекс, Боб и Карл гуляют каждый день. Если Алекс гуляет без шляпы, то Боб гуляет в шляпе. А если Боб гуляет без шляпы, то Карл гуляет в шляпе. Сегодня Боб без шляпы. Кто сегодня в шляпе?
A) Алекс и Карл
Б) только Алекс
В) только Карл
Г) не Алекс и не Карл
Д) невозможно определить
20
На следующих рисунках показаны развёртки куба. На каком из них линия на поверхности куба является замкнутой?

21

На рисунке показан куб, у которого на гранях написаны натуральные числа. Произведения чисел на противоположных гранях одинаковые. Какое наименьшее значение может иметь сумма всех чисел на гранях такого куба?
A) 36 Б) 37 В) 41 Г) 44 Д) 60
22
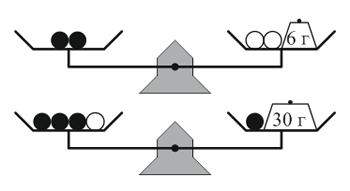
Шесть одинаковых чёрных и три одинаковых белых шарика помещены на чашах двух весов так, как показано на рисунке. Чему равен суммарный вес всех этих девяти шариков?
A) 100 г Б) 99 г В) 96 г Г) 94 г Д) 90 г
23
Роберт сделал следующие пять заявлений. Ровно одно из них ложное. Какое?
A) у моего сына Васи есть 3 сестры
Б) у моей дочери Ани есть 2 брата
В) у моей дочери Ани есть 2 сестры
Г) у моего сына Васи есть 2 брата
Д) у меня 5 детей
24
Боря вписал какое-то целое число в первый кружочек, а затем он вписал числа во все следующие кружочки согласно инструкции:
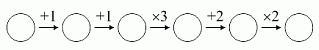
Сколько из шести записанных Борей чисел могут быть кратны 3?
A) ровно 1
Б) 1 или 2
В) ровно 2
Г) 2 или 3
Д) 3 или 4
25
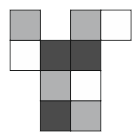
Кусок картона на рисунке свернули в коробку 2×1×1. Какая из следующих коробок не могла получиться?

26
Эмили сделала селфи со своими 8 друзьями. Каждый из 8 друзей оказался на двух или трёх снимках. На каждом селфи ровно 5 её друзей. Сколько селфи сделала Эмили?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
27
Петя и Вася бросают шары в две одинаковые пирамиды из 15 банок. Петя сбил 6 банок с общим количеством очков 25. Вася сбил 4 банки. Сколько очков набрал Вася?
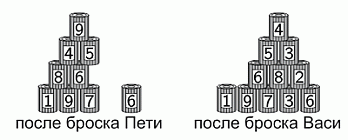
A) 22 Б) 23 В) 25 Г) 26 Д) 28
28
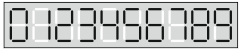
Все цифры на электронных часах изображаются с помощью семи элементов так, как показано на рисунке. Но однажды какие-то два элемента (одни и те же) во всех разрядах перегорели и перестали действовать. В настоящее время часы показывают:

Что они будут показывать через 3 часа 45 минут?

29
Лена строит куб 4×4×4 из 32 белых и 32 чёрных единичных кубиков. Она хочет, чтобы как можно большая часть поверхности этого куба была белой. Какой будет эта часть поверхности?
A) 1/4 Б) 1/2 В) 2/3 Г) 3/4 Д) 7/8
30
У Зины есть два автомата: один меняет 1 белый жетон на 4 красных, а другой меняет 1 красный жетон на 3 белых. Вначале у Зины было 4 белых жетона, а после 11 обменов у нее оказался 31 жетон. Сколько среди них красных жетонов?
A) 21 Б) 17 В) 14 Г) 27 Д) 11