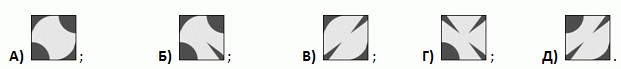
2

Тамара едет из Атауна в Бетаун. По дороге она проезжает мимо следующих указателей. Один из них неправильный. Который?

3

Квадрат на рисунке состоит из белых и серых клеток. Как он будет выглядеть, если серые клетки поменять на белые, а белые – на серые?

4

Миша хочет испечь 24 блинчика для своих друзей на его день рождения. Чтобы испечь 6 блинчиков, нужны 2 яйца. Яйца продаются в коробках по 6 штук. Какое наименьшее число коробок яиц Мише нужно купить?

A) 1       Б) 2       В) 3       Г) 4       Д) 6

5

У Кати есть несколько цепочек, состоящих из 5 или 7 бусинок. Катя хочет связать их в круг, чтобы получились бусы. Сколько бусинок не может быть в полученных бусах?

A) 10       Б) 12       В) 13       Г) 14       Д) 15

6

Федя отразил симметрично букву F относительно вертикальной прямой и относительно горизонтальной прямой на рисунке. Что у него получилось?

7

У Маши было 10 листов бумаги. Она разрезала некоторые их них на 5 частей каждый. В результате всего у неё получилось 22 листа. Сколько листов Маша разрезала?

A) 3       Б) 2       В) 6       Г) 7       Д) 8

8

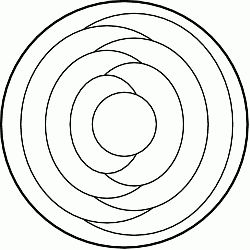
Синди раскрашивает каждую часть круга на рисунке в красный, синий или жёлтый цвет. Части, имеющие общую границу, должны быть окрашены в разные цвета. Внешнюю часть она окрасила в синий цвет. Сколько всего частей Синди окрасит в синий цвет?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

9

В четырёх корзинах находятся 1, 4, 6 и 9 яблок. Какое наименьшее количество яблок нужно переместить между корзинами, чтобы в них яблок стало поровну?

A) 3       Б) 4       В) 5       Г) 6       Д) 7

10

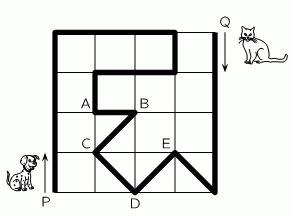
Собака и кошка идут в парке по тропе, отмеченной жирной линией. Они выходят одновременно из точек P и Q соответственно. Собака идёт в три раза быстрее, чем кошка. В какой точке они встретятся?

A) A       Б) B       В) C       Г) D       Д) E

11

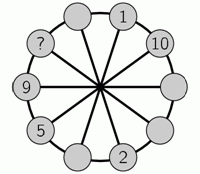
Маша хочет вписать числа от 1 до 10 в кружочки на колесе. Сумма чисел в любых двух соседних кружочках должна быть равна сумме чисел в двух диаметрально противоположных им кружочках (Например, сумма чисел в двух соседних верхних кружочках должна равняться сумме чисел в двух соседних нижних кружочках.). Некоторые числа Маша уже вписала так, как показано на рисунке. Какое число она должна вписать в кружочек со знаком вопроса?

A) 3       Б) 4       В) 6       Г) 7       Д) 8

12

Когда летучая мышь Лиза вылетела из пещеры, цифровые часы показывали 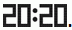Когда она вернулась, то, вися вниз головой, снова увидела на часах 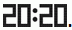Как долго Лиза находилась вне пещеры?

A) 3 ч 28 мин

Б) 3 ч 40 мин

В) 3ч 42 мин

Г) 4 ч 18 мин

Д) 5 ч 42 мин

13

Встретились эльф и тролль. Тролль всегда лжёт, а эльф всегда говорит правду. Они оба произнесли одно из следующих предложений. Какое?

A) Я говорю правду.

Б) Ты говоришь правду.

В) Мы оба говорим правду.

Г) Я всегда лгу.

Д) Только один из нас говорит правду.

14

У Маши ровно 10 белых кубиков, 9 светло-серых и 8 тёмно-серых, все одного размера. Она склеивает все кубики так, чтобы получился большой куб. Какой из следующих кубов у неё может получиться?

15

На следующих диаграммах отмечены жирной линией пути от X до Y. Какой из них самый короткий?

16

Папа кенгуру живёт со своими тремя детьми. Они решают все вопросы путём голосования, и каждый член семьи имеет право на столько голосов, сколько ему лет. Сейчас папе 36 лет, а детям 13, 6 и 4 года. Поэтому папа всегда побеждает. Сколько лет должно пройти, чтобы дети могли выиграть у папы, если они с ним не согласны?

A) 5       Б) 6       В) 7       Г) 13       Д) 14

17

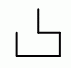
У Жоры есть два одинаковых куска проволоки, показанных на рисунке. Какую из следующих конструкций нельзя получить, спаяв два таких куска?

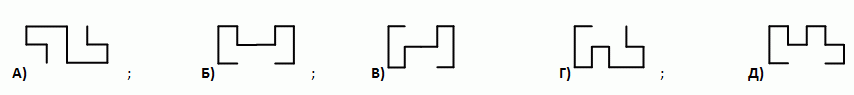
18

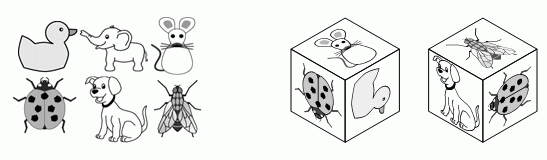
Аня наклеила шесть стикеров на грани кубика. На рисунке показаны эти стикеры и вид кубика с двух сторон. Какой стикер находится на грани, противоположной грани с мышью?

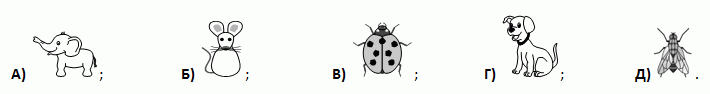
19

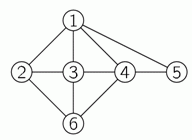
Рисунок показывает дружеские отношения между шестью девочками. Девочек зовут Аня, Бася, Валя, Галя, Дина и Ева. Девочки изображены кружочками с числами. Если какие-то две девочки дружат между собой, то соответствующие кружочки соединены отрезком. Валя, Галя и Ева имеют по 4 подруги. Бася дружит только с Валей и Галей. Каким числом обозначена на рисунке Ева?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

20

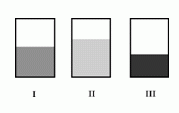
Маша налила одинаковое количество жидкости в три прямоугольных сосуда. Если смотреть на эти сосуды спереди, то кажется, что они имеют одинаковый размер. Но жидкости в них имеют разные уровни. На каком из следующих рисунков показан вид сверху на эти три сосуда?

21

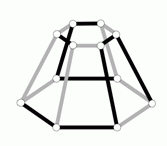
Как выглядит сверху следующая конструкция?

22

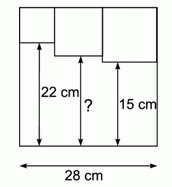
Внутри квадрата расположены три меньших квадрата так, как показано на рисунке. Чему равна длина отрезка, обозначенного знаком вопроса?

A) 17 см       Б) 17,5 см       В) 18 см       Г) 15,5 см       Д) 19 см

23

Будем называть трёхзначное число красивым, если его средняя цифра больше суммы его первой и последней цифры. Какое наибольшее количество последовательных трёхзначных чисел могут оказаться красивыми?

A) 5       Б) 6       В) 7       Г) 8       Д) 9

24

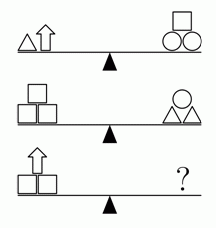
Какой из следующих наборов уравновесит третьи весы?

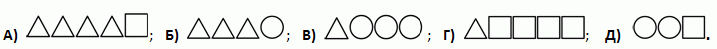
25

Десять школьников заказали по одному шарику мороженого: 4 ванильного, 3 шоколадного, 2 лимонного и 1 манго. Они добавили к мороженому 4 зонтика, 3 вишенки, 2 вафли и 1 клубничку, к каждому шарику что-то ровно одно, так, что все десять сочетаний оказались различным. Какое из следующих сочетаний не могло получиться?

A) шоколадное с вишней

Б) манго с зонтиком

В) ванильное с зонтиком

Г) лимонное с вафлей

Д) ванильное с клубничкой

26

У Вани есть 9 жетонов, с одной стороны они белые, а с другой – чёрные. Изначально жетоны выложены в ряд так, как показано на рисунке. За один ход Ваня может перевернуть любые 3 жетона. За какое наименьшее количество ходов Ваня может добиться того, чтобы сверху все жетоны были одного цвета?

A) 1       Б) 2       В) 3       Г) 4       Д) 5

27

Магнус должен сыграть 15 партий в шахматном турнире. В какой-то момент времени из сыгранных партий он имел половину выигрышей, треть проигрышей и 2 ничьих. Сколько партий ещё оставалось сыграть Магнусу?

A) 2       Б) 3       В) 4       Г) 5       Д) 6

28

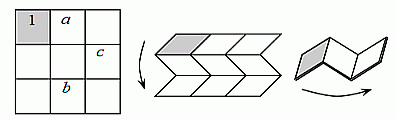
У Вадима имеется квадратный лист бумаги, состоящий из 9 клеток. Он хочет сложить его по линиям клеток сначала по горизонтали, а затем по вертикали, так чтобы серая клетка оказалась сверху (см. рис.). Вадим хочет вписать в клетки числа от 1 до 9 так, чтобы после сгиба квадрата числа в клетках располагались (сверху вниз) в порядке возрастания. Какие числа он должен вписать вместо букв а, b и c?

A) a = 6, b = 4, c = 8

Б) a = 4, b = 6, c = 8

В) a = 5, b = 7, c = 9

Г) a = 4, b = 5, c = 7

Д) a = 6, b = 4, c = 7

29

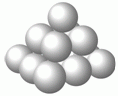
Дима строит пирамиду из одинаковых шариков. Нижний слой представляет собой квадрат из 9 шариков, средний – квадрат из 4 шариков, верхний – 1 шарик. Дима поместил по капле клея во все точки соприкосновения шариков. Сколько таких капель получилось?

A) 20       Б) 24       В) 28       Г) 32       Д) 36

30

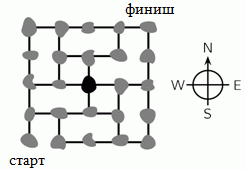
На рисунке показана карта нескольких островов и мостов между ними. Почтальон должен посетить каждый остров ровно один раз. Он начинает путь с острова с пометкой «старт» и хотел бы закончить его на острове с пометкой «финиш». Он только что достиг чёрного острова в центре карты. В каком направлении ему следует двигаться, чтобы завершить свой путь так, как он задумал?

A) на север

Б) на восток

В) на юг

Г) на запад

Д) такого направления не существует