1
У Лизы есть четыре деревянные цифры, из которых можно составить число 2025. Какое наибольшее число она может составить из этих цифр?
A) 2502 Б) 5202 В) 5220 Г) 5502 Д) 5520
2
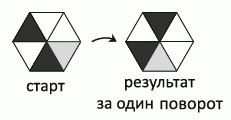
Изабелла поворачивает бумажный шестиугольник каждый раз на одинаковый угол в одном направлении. На рисунке показано, как выглядит фигура после одного такого поворота. Через какое число поворотов из предложенных этот шестиугольник займёт исходное положение?
A) 7 Б) 8 В) 9 Г) 10 Д) 12
3
Саша бросает три игральных кубика и получает сумму 8. На всех трёх кубиках выпали разные числа. Какое число точно не могло выпасть ни на одном из кубиков?

4
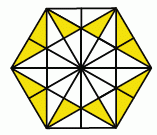
Правильный шестиугольник разделён на треугольники равной площади. Какая по площади часть шестиугольника закрашена?
A) 1/2 Б) 1/3 В) 1/4 Г) 1/5 Д) 1/6
5
Сколько промежутков времени по 12 минут равны 12 часам?
A) 60 Б) 24 В) 12 Г) 10 Д) 6
6
Денису 5 лет. Его брат Доминик на 6 лет старше. Какова будет сумма их возрастов через 7 лет?
A) 26 Б) 27 В) 28 Г) 29 Д) 30
7
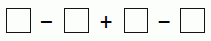
Олег хочет записать цифры 2, 0, 2 и 5 в четыре клетки на рисунке. Какое наименьшее значение может иметь полученное выражение?
A) -7 Б) -6 В) -5 Г) -4 Д) -3
8
В комнате находятся правдолюбы и лжецы. Правдолюбов на 10 человек больше, чем лжецов. Всем задали вопрос: «Вы правдолюб?» и каждый дал ответ. Ответ «Да» дали 20 человек. Сколько лжецов в комнате?
A) 0 Б) 5 В) 15 Г) 20 Д) 25
9
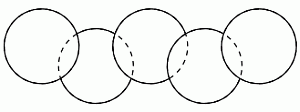
На рисунке изображена фигура, образованная пятью кругами, наложенными друг на друга. Площадь каждого круга равна 8 см2. Площадь каждой секции, образованной наложением кругов, составляет 1 см2. Чему равна площадь, покрытая фигурой?
A) 32 см2 Б) 36 см2 В) 38 см2 Г) 39 см2 Д) 42 см2
10
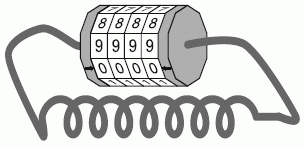
Настоящий код замка велосипеда, показанного на рисунке, — это 0000. Однако, если посмотреть на него под другим углом, он выглядит как 8888. Когда Павел смотрит под этим другим углом на замок своего друга, он видит 2815. Каков настоящий код замка его друга?
A) 4037 Б) 4693 В) 0639 Г) 0693 Д) 9603
11
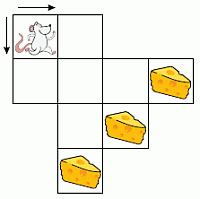
Мышонок Матвей хочет добраться до кусочка сыра. Он может передвигаться только по горизонтали или вертикали, следуя направлениям, указанным стрелками. Сколько разных маршрутов может выбрать Матвей, чтобы добраться до сыра?
A) 3 Б) 5 В) 8 Г) 10 Д) 11
12
В забеге на 60 метров с барьерами установлено 5 барьеров. Первый барьер расположен на расстоянии 12 метров от старта, а расстояние между любыми двумя соседними барьерами составляет 8 м. Какое расстояние от последнего барьера до финиша?
A) 16 м Б) 14 м В) 12 м Г) 10 м Д) 8 м
13
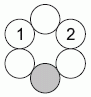
Эдгар хочет записать числа по кругу так, чтобы каждое число равнялось сумме двух соседних. Два числа он уже вписал, как показано на рисунке. Какое число он должен вписать в сером кружочке?
A) 2 Б) -1 В) -2 Г) -3 Д) -5
14
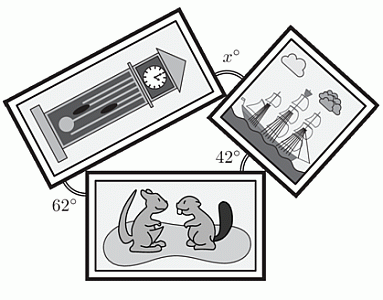
Людмила разместила три прямоугольные картины так, как показано на рисунке. Чему равен угол x?
A) 64 Б) 70 В) 72 Г) 76 Д) 80
15
У Сергея есть две коробки с пронумерованными шарами. В коробке X находятся шары с номерами 1, 2, 6, 7, 10, 11 и 12. В коробке Y — шары с номерами 3, 4, 5, 8 и 9. Какой шар Сергей должен переложить из коробки X в коробку Y, чтобы в обеих коробках средние арифметические номеров шаров увеличились?
A) 6 Б) 7 В) 10 Г) 11 Д) 12
16
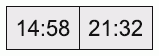
Вася занимается на беговой дорожке с двумя секундомерами. Первый показывает время, прошедшее с начала тренировки, а второй — время, оставшееся до её окончания. В какой-то момент оба секундомера показывают одно и то же время. Чему равно это показание?
A) 17:50
Б) 18:00
В) 18:12
Г) 18:15
Д) 18:20
17
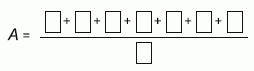
Юля хочет заполнить все клетки на рисунке различными простыми числами, меньшими 20, так, чтобы дробь A оказалась целым числом. Какое наибольшее значение может принимать A?
A) 20 Б) 14 В) 10 Г) 8 Д) 6
18
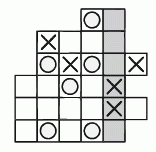
Марат вписывает в ячейки на схеме либо крестик, либо кружок. При этом он следит, чтобы ни в одном столбце, строке или диагонали не было четырёх одинаковых символов подряд. Несколько символов он уже вписал, как показано на рисунке. Какие символы окажутся в сером столбце, когда вся схема будет заполнена?
A) 3 кружочка и 3 крестика
Б) 2 кружочка и 4 крестика
В) 4 кружочка и 2 крестика
Г) 5 кружков и 1 крестик
Д) 1 кружок и 5 крестиков
19
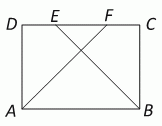
В прямоугольнике ABCD на стороне DC отмечены точки E и F так, что ∠EBA = ∠DFA = 45° и AB + EF = 20 см. Чему равна длина BC?
A) 4 см Б) 6 см В) 8 см Г) 10 см Д) 12 см
20
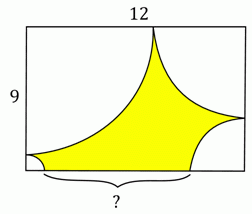
Петя нарисовал по четверти окружности в каждом углу прямоугольника 12 см × 9 см, как показано на рисунке. Чему равна длина отрезка, отмеченного вопросительным знаком?
A) 5 см Б) 6 см В) 7 см Г) 8 см Д) 9 см
21
Дано шестизначное число PAPAYA, в котором разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры. Известно, что
Y = P + P = A + A + A.
Найдите значение выражения
P × A × P × A × Y × A.
A) 432 Б) 342 В) 324 Г) 243 Д) 234
22
За две футбольные тренировки Паша ударил по воротам 17 раз. На первой тренировке 60% всех его ударов оказались успешными, а на второй — 75%. Сколько голов забил Паша на второй тренировке?
A) 6 Б) 7 В) 8 Г) 9 Д) 10
23
Антон каждый день выходит в школу в 8:00. Расстояние от его дома до школы равно 1 км. Если Антон идёт пешком со скоростью 4 км/ч, то приходит за 5 минут до начала уроков. За сколько минут до начала уроков приедет Антон, если поедет в школу на велосипеде со скоростью 15 км/ч?
A) 12 Б) 13 В) 14 Г) 15 Д) 16
24
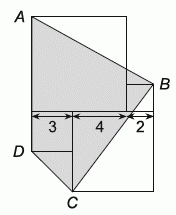
Рита начертила четыре квадрата, как показано на рисунке. Чему равна площадь закрашенного четырехугольника?
A) 54 Б) 60 В) 66 Г) 72 Д) 80
25
р, q, r, s и t являются пятью последовательными положительными целыми числами, но не обязательно в данном порядке. Сумма p и q равна 69, а сумма s и t равна 72. Чему равно r?
A) 29 Б) 31 В) 34 Г) 37 Д) 39
26
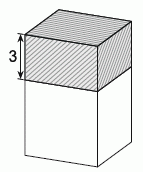
Высоту прямоугольного параллелепипеда уменьшили на 3 см и получили куб. Площадь поверхности фигуры при этом уменьшилась на 60 см2. Чему равен объём исходного прямоугольного параллелепипеда в см3?
A) 75 Б) 125 В) 150 Г) 200 Д) 225
27
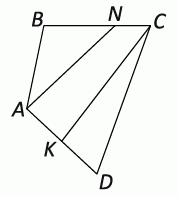
В четырёхугольнике ABCD на сторонах BC и AD отмечены точки N и K соответственно так, что BN = 2NC и AK = KD. Площадь треугольника CKD равна 2, а площадь треугольника ABN равна 6. Чему равна площадь четырёхугольника ABCD?
A) 13 Б) 14 В) 15 Г) 16 Д) 17
28
На четырёх проводах сидит стая птиц, среди которых Кеша, Гоша, Чип и Снежок. Над Кешей сидят 10 птиц, над Гошей — 25 птиц. Под Чипом сидят 5 птиц, а под Снежком — 2 птицы. Количество птиц, сидящих над Снежком, кратно количеству птиц, сидящих под ним. Сколько всего птиц на этих четырёх проводах?
A) 27 Б) 30 В) 32 Г) 37 Д) 40
29
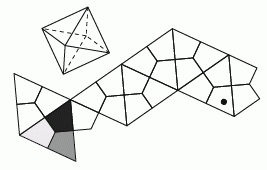
На рисунке показана развёртка октаэдра, где каждая грань разделена на три части. Октаэдр раскрашен тремя цветами: чёрным, тёмно-серым и светло-серым. Цвета расположены так, что части, которые исходят или из одной вершины, или из противоположных, имеют одинаковый цвет. В какой цвет можно покрасить часть, обозначенную точкой?
A) только в чёрный
Б) только в тёмно-серый
В) только в светло-серый
Г) в чёрный или в тёмно-серый
Д) в чёрный или в светло-серый
30
Арина хранит золотые, красные, чёрные, розовые и белые жемчужины в пяти шкатулках. Каждая шкатулка содержит жемчужины только одного цвета. Шкатулки подписаны, как показано на рисунках, и все надписи правдивые. Лиля, подруга Арины, хочет узнать, в какой шкатулке находятся золотые жемчужины. Она может открыть только одну шкатулку, чтобы посмотреть, что внутри. Какую шкатулку ей нужно открыть, чтобы точно узнать, в какой из них золотые жемчужины?
