1
Какое время будет через 17 часов после 17:00 ?
A) 8:00 Б) 10:00 В) 11:00 Г) 12:00 Д) 13:00
2
Несколько девочек стоят по кругу. Лена – четвёртая слева от Яны, она же – седьмая справа от Яны. Сколько девочек стоит по кругу?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
3
Какое число нужно вычесть из числа -17, чтобы получить число -33?
A) -50 Б) -16 В) 16 Г) 40 Д) 50
4
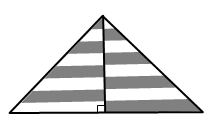
Равнобедренный треугольник на рисунке разбит на полоски равной ширины. Какая его часть является серой?
A) 1/2 Б) 1/3 В) 2/3 Г) 3/4 Д) 2/5
5
Какое из следующих равенств является правильным?
A) 4/1 = 1,4
Б) 5/2 = 2,5
В) 6/3 = 3,6
Г) 7/4 = 4,7
Д) 8/5 = 5,8
6
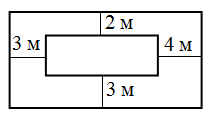
На рисунке показаны два прямоугольника с параллельными сторонами и указаны расстояния между ними. Чему равна разность периметров этих прямоугольников?
A) 12 м Б) 16 м В) 12 м Г) 21 м Д) 24 м
7

Боря дважды согнул лист бумаги, а затем сделал один прокол. Когда он развернул этот лист, то получил лист, изображенный на рисунке выше. Как Боря сворачивал лист бумаги?

8
Сумма трёх различных натуральных чисел равна 7. Чему равно их произведение?
A) 12 Б) 10 В) 9 Г) 8 Д) 6
9

Рита сделала декорацию из четырёх красных и белых «сердечек», наклеив их друг на друга (см. рис.). Площади сердечек равны 1 см2, 4 см2, 9 см2 и 16 см2. Чему равна площадь красной части декорации?
A) 9 см2
Б) 10 см2
В) 11 см2
Г) 12 см2
Д) 13 см2
10
У Вали есть 20 рублей, а у её четырёх сестёр – по 10 рублей. Сколько рублей Вале нужно дать каждой из своих сестёр, чтобы у всех пяти девочек денег стало поровну?
A) 2 Б) 4 В) 5 Г) 8 Д) 10
11

Божья коровка и муравей ползут по шесту, начав с разных его сторон. Божья коровка проползла 3/4 длины шеста, а муравей – 2/3. Какая часть длины шеста равна расстоянию между ними?
A) 3/8 Б) 1/12 В) 5/7 Г) 1/2 Д) 5/12
12
Среди посетителей детского театра взрослые составили одну шестую часть. Две пятых от общего числа детей составили мальчики. Какую часть от числа всех посетителей составили девочки?
A) 1/2 Б) 1/3 В) 1/4 Г) 1/5 Д) 2/5
13
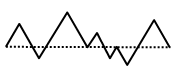
На рисунке чёрная ломаная и штриховой отрезок образуют 7 равносторонних треугольников. Длина штрихового отрезка равна 20 см. Чему равна длина чёрной ломаной?
A) 25 см Б) 30 см В) 35 см Г) 40 см Д) 45 см
14
Сёстрам Эмме, Еве, Рите и Зине 3, 8, 12 и 14 лет, не обязательно в таком же порядке. Эмма моложе Риты. Сумма возрастов Зины и Эммы делится на 5. Сумма возрастов Зины и Риты тоже делится на 5. Сколько лет Еве?
A) 14 Б) 12 В) 8 Г) 5 Д) 3
15
В конкурсе «Кенгуру» в нашем районе приняли участие более 800 школьников. Девочки составили ровно 35% от числа участников, а мальчиков оказалось на 252 человека больше, чем девочек. Сколько всего школьников нашего района участвовало в «Кенгуру»?
A) 802 Б) 810 В) 822 Г) 824 Д) 840
16
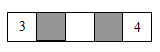
Рита хочет вписать числа во все клетки на рисунке. Два из них она уже вписала. Рита хочет также, чтобы сумма всех чисел равнялась 35, чтобы сумма чисел в первых трёх клетках равнялась 22, а сумма чисел в последних трёх клетках равнялась 25. Чему будет равно произведение чисел в серых клетках?
A) 63 Б) 108 В) 0 Г) 48 Д) 39
17
Симона хочет разрезать ленту на 9 равных частей и отметила на ленте соответствующие точки разрезания. Барбара хочет разрезать эту же ленту на 8 равных частей и также отметила на ней соответствующие точки разрезания. Карл взял и разрезал ленту во всех отмеченных точках. Сколько всего кусков ленты получилось в результате?
A) 15 Б) 16 В) 17 Г) 18 Д) 19
18
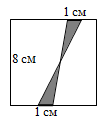
Два отрезка длины 1 см отмечены на противоположных сторонах квадрата со стороной 8 см. Концы отрезков соединили так, как показано на рисунке. Чему равна сумма площадей двух серых треугольников?
A) 2 см2
Б) 4 см2
В) 4,2 см2
Г) 6,4 см2
Д) 8 см2
19
Тихон занимается спортом и составляет график пробежек. Он хочет бегать ровно два раза в неделю в одни и те же дни недели, но так, чтобы не случалось пробежек два дня подряд. Сколько таких различных графиков существует?
A) 16 Б) 14 В) 12 Г) 10 Д) 8
20
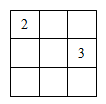
Мария хочет вписать числа в клетки таблицы 3 × 3 так, чтобы суммы чисел в любых двух клетках, имеющих общую сторону, были одинаковы. Она уже вписала два числа так, как показано на рисунке. Чему будет равна сумма всех чисел в таблице?
A) 18 Б) 20 В) 21 Г) 22 Д) 23
21
Все углы треугольника выражаются различными целыми числами градусов. Какое наименьшее значение может иметь сумма меньшего и большего углов такого треугольника?
A) 61° Б) 90° В) 91° Г) 120° Д) 121°
22
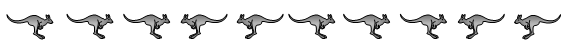
В ряд стоят 10 кенгуру так, как показано на рисунке. В некоторый момент времени какие-то два кенгуру, которые стоят рядом и смотрят друг на друга, меняются местами, но не поворачиваются. Затем снова какие-то два кенгуру, которые стоят рядом и смотрят друг на друга, меняются местами, но не поворачиваются и т.д. Какое число таких перемен мест может быть сделано до того, как они станут невозможны?
A) 15 Б) 16 В) 18 Г) 20 Д) 21
23
У Дианы есть 9 чисел: 1, 2, 3, 4, 5, 6, 7, 8 и 9. К некоторым из них она прибавила 2, а к остальным прибавила 5. Какое наименьшее количество различных результатов у неё могло получиться?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
24
Через каждые 3 минуты из аэропорта к центру города по одному и тому же маршруту одновременно отправляются автобус и маршрутное такси. Автобусу на весь путь требуется 60 минут, а маршрутке – 35 минут. Сколько автобусов обгоняет по пути маршрутка (не считая автобус, с которым она одновременно выезжает)?
A) 8 Б) 9 В) 10 Г) 11 Д) 13
25

Скатерть Олеси украшена симметричным узором, показанным на рисунке. Какой процент площади скатерти является чёрным?
A) 16% Б) 24% В) 25% Г) 32% Д) 36%
26
Последовательность 2, 3, 6, 8, 8, … получена следующим образом. Два первых числа равны 2 и 3, каждое следующее число равно последней цифре произведения двух предыдущих чисел. Найдите 2017-й член этой последовательности.
A) 2 Б) 3 В) 4 Г) 6 Д) 8
27
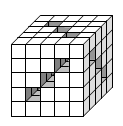
У Миши было 125 одинаковых кубиков. Он склеил из них куб с девятью сквозными прямолинейными тоннелями, как показано на рисунке. Сколько кубиков у него остались не использованными?
A) 52 Б) 45 В) 42 Г) 39 Д) 36
28
Два бегуна бегут с постоянной скоростью во встречных направлениях по круговой дорожке длиной 720 метров. Первый бегун пробегает круг за 4 минуты, а второй – за 5 минут. Сколько метров пробегает второй бегун между двумя последовательными встречами с первым бегуном?
A) 355 Б) 350 В) 340 Г) 330 Д) 320
29
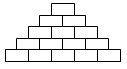
Саша хочет вписать натуральные числа в ячейки на рисунке так, чтобы, начиная со второго снизу ряда, каждое число являлось суммой двух чисел в соседних ячейках, расположенных непосредственно снизу от него. Какое наибольшее количество нечётных чисел может вписать Саша?
A) 5 Б) 7 В) 8 Г) 10 Д) 11
30
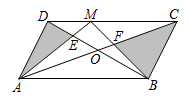
Параллелограмм ABCD на рисунке имеет площадь S. Диагонали пересекаются в точке O. На стороне DC выбрана точка M. Отрезки AM и DB пересекаются в точке E, а отрезки BM и AC – в точке F. Сумма площадей треугольников AED и BFC равна 1/3·S. Чему равна площадь четырехугольника EOFM?
A) 1/6·S
Б) 1/8·S
В) 1/10·S
Г) 1/12·S
Д) 1/14·S