1
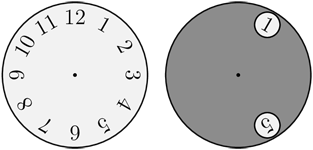
Серым кругом с двумя отверстиями накрыли циферблат таких же размеров, как показано на рисунке. Круг повернули вокруг центра так, что в одном из отверстий оказалась число 10. Какие из следующих чисел можно увидеть в другом отверстии?
A) 2 или 6
Б) 3 или 7
В) 3 или 6
Г) 1 или 9
Д) 2 или 7
2
Марии пришлось бежать, чтобы сесть в вагон метро. Затем она проехала две остановки и пошла в школу пешком. Какой из следующих графиков скорость-время лучше всего представляет ее путешествие?

3
Натуральные числа m и n - нечётные. Какое из следующих целых чисел также нечётное?
A) m(n + 1)
Б) (m + 1)(n + 1)
В) m + n + 2
Г) m(n + 2)
Д) m + n
4
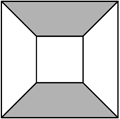
В большом квадрате со стороной 10 см находится меньший квадрат со стороной 4 см, как показано на рисунке. Соответствующие стороны этих квадратов параллельны. Сколько процентов (по площади) большого квадрата составляет его серая часть?
A) 25% Б) 30% В) 40% Г) 42% Д) 45%
5
Сегодня четверг. Какой день недели будет через 2023 дня?
A) вторник Б) среда В) четверг Г) пятница Д) суббота
6

Прямоугольник на рисунке разбит на 30 равных квадратных клеток. Периметр заштрихованной области равен 240 см. Чему равна площадь данного прямоугольника?
A) 480 см2
Б) 750 см2
В) 1080 см2
Г) 1920 см2
Д) 2430 см2
7
Возраст семьи из пяти человек в сумме составляет 80 лет. Двум младшим детям 6 и 8 лет. Сколько лет в сумме было членам этой семьи семь лет назад?
A) 35 Б) 36 В) 45 Г) 46 Д) 66
8
Деревянный забор состоит из ряда вертикальных и горизонтальных досок. Первая и последняя доски в заборе вертикальные. Любые две соседние вертикальные доски соединены четырьмя горизонтальными. Каким из следующих чисел может быть общее число досок в заборе?
A) 95 Б) 96 В) 97 Г) 98 Д) 99
9
Буквы a и b в уравнении
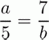
нужно заменить натуральными числами так, чтобы это уравнение превратилось в правильное равенство. Сколькими способами это можно сделать?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
10
После того, как я сыграл 200 партий в шахматы, количество моих побед составляет ровно 49%. Какое наименьшее количество дополнительных партий мне нужно сыграть, чтобы увеличить процент выигрышей ровно до 50% (при условии, что все дополнительные партии будут выиграны)?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
11
Дженни пытается экономить воду. Она сократила время, проводимое в душе, на четверть. Она также снизила напор воды в душе, чтобы на четверть уменьшить объём вытекающей воды за единицу времени. На какую часть Дженни уменьшила общее количество потребляемой воды?
A) на 1/4
Б) на 3/8
В) на 5/8
Г) на 5/12
Д) на 7/16
12
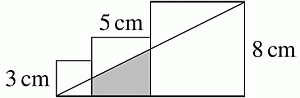
На рисунке показаны три квадрата со сторонами 3 см, 5 см и 8 см. Чему равна площадь серой трапеции?
A) 13 см2
Б) 55/4 см2
В) 61/4 см2
Г) 65/4 см2
Д) 69/4 см2
13
Проволоку длиной 95 м разрезали на три куска так, чтобы каждый следующий кусок был на 50% длиннее предыдущего. Какова длина самого длинного куска?
A) 36 м Б) 42 м В) 45 м Г) 46 м Д) 48 м
14
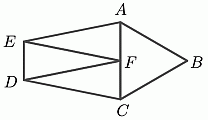
Пятиугольник ABCDE разбит на четыре треугольника с равными периметрами. Треугольник ABC равносторонний, а треугольники AEF, DFE и CDF — равные равнобедренные. Как относится периметр пятиугольника ABCDE к периметру треугольника ABC?
A) 2 : 1
Б) 3 : 2
В) 4 : 3
Г) 5 : 3
Д) 5 : 2
15
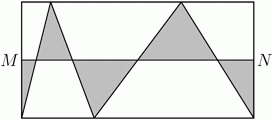
Точки M и N ─ середины двух сторон прямоугольника (см. рис.). Какая часть площади прямоугольника закрашена?
A) 1/6 Б) 1/5 В) 1/4 Г) 1/3 Д) 1/2
16
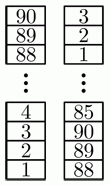
На столе стоит башня, состоящая из блоков, пронумерованных числами от 1 до 90 снизу вверх. Боря строит новую башню следующим образом. Он берёт три блока с вершины исходной башни и кладёт их на стол в качестве основания новой башни. Затем он берёт следующие три верхних блока из оставшейся части исходной башни и кладёт их на вершину новой башни, как показано на рисунке, и т. д. Сколько блоков будет между блоками 39 и 40 в новой башне?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
17
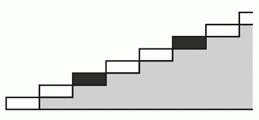
Каждая третья ступенька лестницы с 2023 ступеньками окрашена в чёрный цвет. Начало лестницы показано на рисунке. Аня поднимается по ступенькам по одной, начиная с правой или левой ноги, чередуя шаги левой и правой ногой. Какое наименьшее число чёрных ступеней она может пройти правой ногой?
A) 0 Б) 333 В) 336 Г) 337 Д) 674
18
Будем называть двузначное число бесстепенным, если ни одна из его цифр не может быть записана как целое число в степени, большей 1. Например, число 53 является бесстепенным, а число 54 не является бесстепенным, поскольку 4 = 22. Какое из следующих чисел является общим делителем наименьшего и наибольшего двузначных бесстепенных чисел?
A) 3 Б) 5 В) 72 Г) 11 Д) 13
19
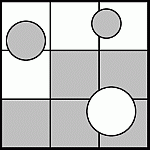
Квадрат со стороной 30 см разбит на 9 одинаковых меньших квадратов. В исходном квадрате находятся 3 круга: радиуса 5 см (внизу справа), 4 см (вверху слева) и 3 см (вверху справа), как показано на рисунке. Чему равна площадь серой части исходного квадрата?
A) 400 см2
Б) 500 см2
В) (400+50π) см2
Г) (500-25π) см2
Д) (500+25π) см2
20
Тима вычисляет среднее арифметическое значение пяти различных простых чисел. Какое наименьшее ЦЕЛОЕ значение он может получить?
A) 2 Б) 5 В) 6 Г) 12 Д) 30
21
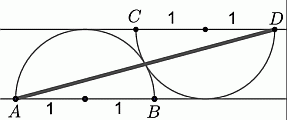
На рисунке показаны две соприкасающиеся полуокружности радиуса 1 с параллельными диаметрами АВ и CD. Чему равен квадрат длины отрезка AD?
A) 16
Б) 8 + 4√3
В) 12
Г) 9
Д) 5 + 2√3
22
Машина «Кенгуру» выполняет следующие операции. Если в машину введены 4 неотрицательных целых числа, она дописывает к ним наименьшее неотрицательное число, отличное от данных четырёх чисел. Затем она дописывает наименьшее неотрицательное целое число, отличное от четырёх предыдущих чисел и повторяет этот процесс снова и снова. Жора ввёл в машину числа 2, 0, 2, 3. Каким будет 2023-е число в полученном списке?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
23
Из прямоугольника на координатной плоскости с вершинами в точках (0, 0), (100, 0), (100, 50) и (0, 50) вырезан круг радиуса 10 с центром в точке (75, 30). Прямая y=kx+b, проходящая через центр круга, делит оставшуюся часть прямоугольника на две равновеликие части. Чему равен угловой коэффициент k этой прямой?
A) 1/5 Б) 1/3 В) 1/2 Г) 2/5 Д) 2/3
24
Когда телефон Мартина полностью заряжен, он разряжается за 32 часа, если используется только для телефонных звонков, через 20 часов, если используется только для интернета, и через 80 часов, если он не используется вообще. Мартин сел в поезд с полузаряженным телефоном. Находясь в поезде, он треть времени на поездку провёл в интернете, треть времени разговаривал по телефону и треть времени телефоном не пользовался. В результате, его телефон разрядился ровно в тот момент, когда поезд прибыл в пункт назначения. Сколько часов заняло путешествие на поезде?
A) 10 Б) 12 В) 15 Г) 16 Д) 18
25
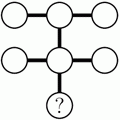
Семь различных однозначных чисел записаны в кружочках данной диаграммы, по одному числу в кружочке. Произведения трёх чисел в каждой из двух строк и среднем столбце, состоящих из трёх чисел, одинаковы. Какое число записано в кружочке со знаком вопроса?
A) 2 Б) 3 В) 4 Г) 6 Д) 8
26
Лёва нарисовал замкнутый путь на поверхности прямоугольного параллелепипеда, а затем развернул его поверхность. Какая из следующих развёрток НЕ может быть развёрткой данного параллелепипеда?

27
Сколько существует трёхзначных натуральных чисел, таких, что при вычитании из них суммы их цифр получается трёхзначное число, все цифры которого одинаковы?
A) 1 Б) 2 В) 3 Г) 20 Д) 30
28

Сколькими способами можно прочитать слово BANANA в следующей таблице, перемещаясь из одной клетки в другую, соседнюю по стороне? Клетки можно посещать более одного раза.
A) 14 Б) 28 В) 56 Г) 84 Д) другой ответ
29
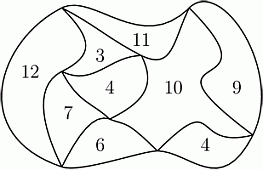
На рисунке показана карта парка. Парк разделён на части. Число внутри каждой части указывает её периметр в км. Каков внешний периметр парка?
A) 22 км
Б) 26 км
В) 28 км
Г) 32 км
Д) другой ответ
30
Полина хочет вписать целые числа от 1 до 9 в девять клеток строки так, чтобы суммы чисел в любых трёх подряд идущих клетках были кратны 3. Сколькими способами она может это сделать?

A) 64
Б) 63
В) 29
Г) 6∙5∙4∙3∙2∙1
Д) 9∙8∙7∙6∙5∙4∙3∙2∙1