1
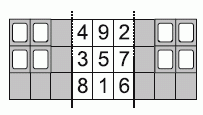
На створках карточки на рисунке, есть прозрачные окошки. Чему равна сумма чисел, которые видны через окошки листовки, когда её створки сложены?
A) 7 Б) 9 В) 12 Г) 14 Д) 15
2
Основание треугольника увеличили на 50%, а его высоту уменьшили на одну треть. Чему равно отношение площади полученного треугольника к площади исходного треугольника?
A) 2:1 Б) 1:1 В) 1:2 Г) 1:3 Д) 1:4
3
В каком из следующих шестиугольников ровно одна треть площади чёрная и ровно половина площади белая?

4
Конкурс «Кенгуру» проводится каждый год в третий четверг марта. Какое самое раннее число может выпасть на этот день?
A) 14 марта
Б) 15 марта
В) 20 марта
Г) 21 марта
Д) 22 марта
5
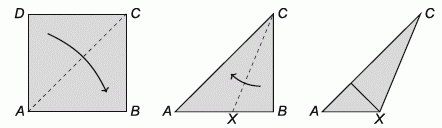
Лёша складывает квадрат по диагонали, получая треугольник. Затем он делает ещё один сгиб так, чтобы одна из коротких сторон этого треугольника легла на его длинную сторону, образуя новый, меньший треугольник AXC. Чему равен угол ∠AXC?
A) 108° Б) 112,5° В) 120° Г) 145° Д) 157,5°
6
Согласно рецепта, для приготовления 1 стакана риса необходимо 1½ стакана воды. Руслан хочет приготовить 1½ стакана риса. Сколько стаканов воды ему нужно?
A) 1 Б) 1¼ В) 1¾ Г) 2¼ Д) 2½
7
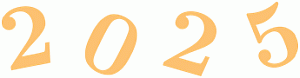
У Лизы есть четыре деревянные цифры, из которых можно составить число 2025. Сколько различных чисел, больших 2025, она может составить из этих цифр?
A) 3 Б) 6 В) 8 Г) 9 Д) 11
8
В 4-значном числе 80☐☐ отсутствуют последние две цифры. Число делится на 8 и 9. Чему равно произведение этих двух отсутствующих цифр?
A) 6 Б) 16 В) 20 Г) 24 Д) 48
9
Лёня держит дома собак, кроликов и кошек. Восемь из его питомцев — не собаки, пять — не кролики, а семь — не кошки. Сколько всего питомцев у Лёни?
A) 10 Б) 11 В) 15 Г) 16 Д) 20
10
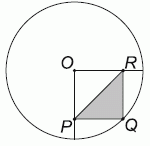
Дана окружность с центром в точке O и радиусом 10 см. Внутри окружности построен квадрат OPQR, где Q — точка на окружности. Чему равна площадь закрашенного треугольника PQR?
A) 12,5 см2
Б) 25 см2
В) 50 см2
Г) 75 см2
Д) 100 см2
11

У спортсмена есть коллекция из двух золотых и пяти серебряных медалей. Каждая медаль имеет свой номер от 1 до 7. На рисунке показаны 6 чёрно-белых фотографий этих медалей, и известно, что на каждой фотографии есть ровно одна золотая медаль. Чему равна сумма номеров двух золотых медалей?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
12

Анна смотрит на фотографию на своём смартфоне. Изображение имеет отношение длин сторон 16:9 и заполняет весь экран. Когда она поворачивает смартфон, изображение становится меньше. Какую часть экрана занимает уменьшенная картинка?
A) 3/4 Б) 9/16 В) 27/64 Г) 32/81 Д) 81/256
13
Катя и Тимофей сегодня отмечают свои дни рождения. Тимофей заметил, что 1/19 возраста Кати равна 1/17 его возраста. Сумма их возрастов больше 40, но меньше 100. Сколько лет Кате?
A) 19 Б) 34 В) 38 Г) 57 Д) 76
14
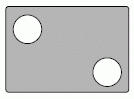
Павел сделал 27 выстрелов по двум мишеням и промахнулся 9 раз. 50% выстрелов, которые он направлял в верхнюю левую мишень, и 80% выстрелов, которые он направлял в нижнюю правую мишень, были успешными. Сколько раз Павел попал в верхнюю левую мишень?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
15
У Александры есть сумка с 18 шариками, пронумерованными числами от 1 до 18. Какое минимальное количество шариков она должна достать, чтобы быть уверенной, что среди них будет хотя бы три шарика с простыми числами?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
16
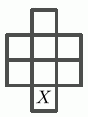
Денис хочет разместить числа от 1 до 8 в ячейках сети на рисунке, по одному числу в каждой ячейке. Он хочет, чтобы ячейки, в которых находятся два последовательных числа, не имели общих сторон или вершин. Какие из чисел Денис может разместить в ячейке, помеченной буквой X?
A) 1 или 8
Б) 2 или 7
В) 3 или 6
Г) 4 или 5
Д) 7 или 8
17
Число N является наибольшим шестизначным целым числом, произведение всех цифр которого равно 180. Чему равна сумма цифр числа N?
A) 21 Б) 22 В) 23 Г) 24 Д) 25
18
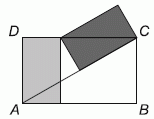
Два закрашенных прямоугольника на рисунке равны. Каждый из них имеет площадь равную 4. Чему равна площадь большого прямоугольника ABCD?
A) 10 Б) 8√3 В) 8 Г) 12 Д) 4√3
19
Произведение трёх простых чисел в 11 раз больше их суммы. Найдите наибольшее возможное значение, которое может иметь эта сумма.
A) 14 Б) 17 В) 21 Г) 25 Д) 26
20
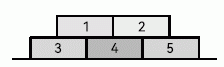
На земле лежат пять кирпичей, как показано на рисунке. Пётр может убрать кирпич только в том случае, если на нём нет других кирпичей. Он убирает по одному кирпичу, выбранному случайным образом, пока на земле не останется ни одного кирпича. Чему равна вероятность того, что кирпич с номером 4 будет убран третьим? (Вероятность равна отношению числа благоприятных исходов к числу всех исходов, если все исходы равновозможны.)
A) 1/3 Б) 1/4 В) 1/5 Г) 1/6 Д) 1/8
21
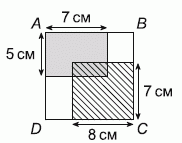
В квадрате ABCD находятся два прямоугольника: один – серый, а другой – заштрихованный. Размеры прямоугольников приведены на рисунке. Площадь их пересечения равна 18 см2. Чему равен периметр квадрата ABCD?
A) 28 см Б) 34 см В) 36 см Г) 38 см Д) 40 см
22
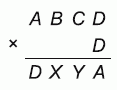
Четырёхзначное число ABCD при умножении на его последнюю цифру D даёт новое четырёхзначное число DXYA, в котором цифры разрядов тысяч и единиц поменялись местами. Сколько существует четырёхзначных чисел ABCD, обладающих таким свойством?
A) 1 Б) 2 В) 9 Г) 10 Д) 11
23
Дано шестизначное число ABCDEF, составленное из цифр 1, 2, 3, 4, 5 и 6 без повторений. Оно обладает следующими свойствами: число AB делится на 2, число ABC делится на 3, число ABCD делится на 4, число ABCDE делится на 5, полное число ABCDEF делится на 6. Чему равна цифра F?
A) 2
Б) 4
В) 6
Г) обе цифры 2 и 4 возможны
Д) обе цифры 4 и 6 возможны
24
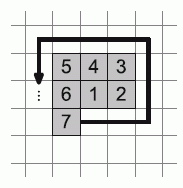
Даниил нумерует клетки в школьной тетрадке. Каждая клетка имеет сторону длиной 0,5 см. Он начинает с клетки, в которую ставит единицу, а затем продолжает нумерацию 2, 3, 4, 5 и так далее, двигаясь против часовой стрелки, как показано на рисунке. Даниил остановился, когда пронумеровал 2025 клеток, и рассматривает фигуру, получившуюся из пронумерованных клеток. Чему равен её периметр?
A) 25 см Б) 45 см В) 80 см Г) 90 см Д) 180 см
25
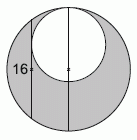
На рисунке два круга касаются внутренним образом. Через точку касания проведён диаметр большего круга. Хорда большего круга параллельна данному диаметру, имеет длину 16 и касается меньшего круга. Найдите площадь серой фигуры.
A) 36 π
Б) 49 π
В) 64 π
Г) 81 π
Д) Недостаточно предоставленной информации
26
Дана последовательность чисел a1, a2, a3, a4, ... , a10, в которой начиная с третьего элемента, каждый следующий элемент является средним арифметическим всех предыдущих чисел. То есть, a3 – это среднее арифметическое a1 и a2, a4 – это среднее арифметическое a1, a2 и a3, и так далее. Известно, что a1 = 8 и a10 = 6. Чему равно число a2?
A) 28 Б) 32 В) 38 Г) 44 Д) 50
27
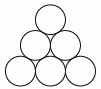
Шесть окружностей расположены в форме треугольника. Иван вписал в них числа от 1 до 6 так, что суммы чисел на всех сторонах этого треугольника оказались одинаковыми. Затем он вычислил сумму чисел в вершинах этого треугольника. Сколько различных значений у него могло получиться?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
28
На празднике находятся 12 детей, среди которых три пары близнецов. Сколькими способами можно распределить между ними шесть синих и шесть красных шляп, что бы каждому близнецу в паре достались шляпы одного цвета?
A) 72 Б) 86 В) 92 Г) 102 Д) 132
29
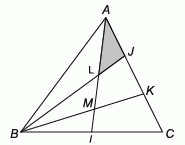
Площадь треугольника ABC равна 60. Точка I является серединой стороны BC, а точки J и K делят сторону AC на три равных отрезка. Точка L является точкой пересечения AI и BJ. Чему равна площадь треугольника ALJ?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
30

Анастасия заполняет таблицу 2 × 4 числами от 1 до 8. При этом каждое число должно быть меньше, чем число справа от него, и меньше, чем число под ним. Сколькими способами она может это сделать?
A) 6 Б) 8 В) 10 Г) 12 Д) 14