1
Каждый год днём проведения конкурса «Кенгуру» является третий четверг марта. Назовите самую раннюю возможную дату проведения конкурса.
A) 14 марта Б) 15 марта В) 20 марта Г) 21 марта Д) 22 марта
2
Контейнеровоз «Фабиола» является одним из самых больших контейнеровозов в мире. Он может перевозить 12500 контейнеров. Если их поставить вплотную друг за другом, то получится цепочка длиной около 75 км. Какова приблизительно длина одного контейнера?
A) 6 м Б) 16 м В) 60 м Г) 160 м Д) 600 м
3
Если a, b, c – длины линий на рисунке, то:
A) a<b<c
Б) a<c<b
В) b<a<c
Г) b<c<a
Д) c<b<a
4
Найдите среднее арифметическое чисел 2/3 и 4/5.
A) 11/15 Б) 7/8 В) 3/4 Г) 9/15 Д) 5/8
5
В числе года 2014 последняя цифра больше суммы остальных его цифр. Какое наименьшее число лет назад выполнялось такое же свойство?
A) 1 Б) 3 В) 5 Г) 7 Д) 11
6
Сторона меньшего шестиугольника на рисунке в 2 раза меньше стороны большего шестиугольника. Площадь меньшего шестиугольника равна 4 см2. Чему равна площадь большего шестиугольника?
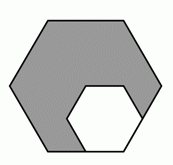
A) 16 см2 Б) 14 см2 В) 12 см2 Г) 10 см2 Д) 8 см2
7
Что является отрицанием утверждения: «Каждый решил более 20 задач»?
A) Никто не решил более 20 задач
Б) Кто-то решил менее 21 задачи
В) Каждый решил менее 21 задачи
Г) Кто-то решил ровно 20 задач
Д) Кто-то решил менее 20 задач
8
На координатной плоскости построен квадрат. Точки (-1; 0) и (5; 0) являются концами одной из его диагоналей. Какая из следующих точек является вершиной этого квадрата?
A) (2; 0) Б) (2; 3) В) (2; –6) Г) (3; 5) Д) (3; –1)
9
В некоторой деревне отношение числа мужчин к числу женщин равно 2:3, а отношение числа женщин к числу детей равно 8:1. Чему равно отношение числа взрослых (женщин и мужчин) к числу детей?
A) 5:1 Б) 10:3 В) 12:1 Г) 13:1 Д) 40:3
10
Обод большого колеса велосипеда имеет длину 4,2 метра, а маленького 0,9 метра. В некоторый момент клапаны обоих колёс оказались в самом нижнем положении. Какое наименьшее расстояние нужно проехать на этом велосипеде, чтобы оба клапана на колёсах снова оказались в самом нижнем положении?
A) 4,2 м Б) 6,3 м В) 12,6 м Г) 25,2 м Д) 37,8 м
11
В этом году сумма возрастов бабушки, её дочери и её внучки равна 100 лет, причём возраст каждой из них является степенью числа 2. В каком году родилась внучка?
A) 1998 Б) 2006 В) 2010 Г) 2012 Д) 2013
12
Коля вешает на стене прямоугольные картины. К верхним углам каждой из них он прикрепил концами верёвку длиной 2 м и повесил все картины на гвозди, вбитые в стену на высоте 2,5 м от пола так, что нижняя сторона картины параллельна полу. У какой из следующих картин нижняя её сторона висит ближе всего к полу? (Размеры приведены в см: длина × высота.)
A) 60 × 40
Б) 120 × 50
В) 120 × 90
Г) 160 × 60
Д) 160 × 100
13
Шестеро студенток снимают квартиру, в которой есть две ванные комнаты. Они просыпаются и начинают умываться ровно в 7:00. На это у них уходит 9, 11, 13, 18, 22 и 23 минуты соответственно. Никакие двое не могут пользоваться одной и той же ванной одновременно. После того, как умылась последняя, они садятся завтракать. В какое самое раннее время может начаться их завтрак?
A) 7:48 Б) 7:49 В) 7:50 Г) 7:51 Д) 8:03
14
Площадь серой части правильного восьмиугольника на рисунке равна 3 см2. Чему равна площадь всего восьмиугольника (в см2)?
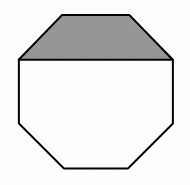
A) 8 + 4√2 Б) 9 В) 8√2 Г) 12 Д) 14
15
В Африке обнаружен новый вид крокодила. Треть его длины составляет хвост. Голова крокодила имеет длину 93 см, что равно четверти его длины без хвоста. Какова длина этого крокодила?
A) 558 см Б) 496 см В) 490 см Г) 372 см Д) 186 см
16
На рисунке изображён специальный кубик. Суммы чисел на его противоположных гранях одинаковые. Все числа на гранях, которые не видны на рисунке, являются простыми. Какое число находится на левой грани (противоположной грани с числом 14)?
A) 11 Б) 13 В) 17 Г) 19 Д) 23
17
Аня прошла расстояние в 8 км со скоростью 4 км/ч. Затем она побежала со скоростью 8 км/ч. Сколько времени она должна бежать, чтобы средняя скорость на всём пути оказалась равной 5 км/ч?
A) 15 минут Б) 20 минут В) 30 минут Г) 35 минут Д) 40 минут
18
Шахматист сыграл 40 партий и набрал 25 очков (за победу в партии присуждается 1 очко, за ничью – 0,5 очка, за проигрыш – 0 очков.) На сколько больше партий он выиграл, чем проиграл?
A) 5 Б) 7 В) 10 Г) 12 Д) 15
19
Тройняшки Джейн, Дэнни и Энн хотели купить одинаковые шляпы. Однако Джейн не хватало одной трети цены, Дэнни – одной пятой, а Энн – одной четвёртой. Но когда цена шляпы стала на 9,40 EUR меньше, сёстры сложили свои сбережения, и им хватило ровно на 3 шляпы без сдачи. Какова была цена шляпы до удешевления?
A) 12 EUR Б) 16 EUR В) 28 EUR Г) 36 EUR Д) 112 EUR
20
Пусть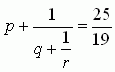 
, где p, q, r – натуральные числа. Чему равно произведение pqr?
A) 6 Б) 10 В) 18 Г) 36 Д) 42
21
Сколько всего существует способов заменить буквы цифрами (одинаковые буквы – одинаковыми цифрами, разные буквы – разными цифрами) в левой части равенства
N x U x (M + B + E + R) = 33,
чтобы оно было правильным?
A) 12 Б) 24 В) 30 Г) 48 Д) 60
22
Какое наименьшее число отрезков с концами в точках, отмеченных на рисунке, нужно дорисовать, чтобы из всех точек выходило одинаковое число отрезков?
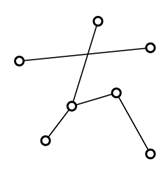
A) 4 Б) 5 В) 6 Г) 9 Д) 10
23
На рисунке один и тот же куб показан с двух разных сторон. Он состоит из 27 кубиков (некоторые из них белые, другие – чёрные). Какое наибольшее число чёрных кубиков может иметь этот куб?
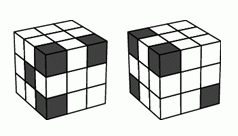
A) 5 Б) 7 В) 8 Г) 9 Д) 10
24
На некотором острове все лягушки либо зелёные, либо синие. После того как число синих лягушек увеличилось на 60%, а число зелёных лягушек уменьшилось на 60%, отношение числа синих лягушек к числу зелёных поменялось на обратное. На сколько процентов изменилось общее число лягушек на острове?
A) 0% Б) 20% В) 30% Г) 40% Д) 50%
25
Том записал несколько различных натуральных чисел, не превосходящих 100. Известно, что их произведение не делится на 18. Какое наибольшее количество чисел мог записать Том?
A) 5 Б) 17 В) 68 Г) 69 Д) 90
26
Рассмотрим все треугольники, у которых вершинами являются какие-то три вершины куба, не лежащие (все три) на одной и той же грани данного куба. Чему равно число таких треугольников?
A) 16 Б) 24 В) 32 Г) 40 Д) 48
27
Через точку P проведена касательная PT к окружности, секущая PA, проходящая через центр O данной окружности, и биссекриса PB угла APT (см. рис.).
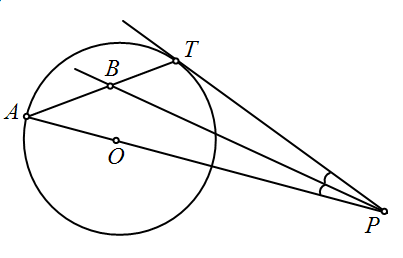
Найдите величину угла TBP.
A) 30° Б) 45° В) 60° Г) 75° Д) зависит от положения точки P
28
Выпишем в порядке возрастания все 7-значные числа, в записи которых используется по разу каждая из цифр от 1 до 7. Чему равно последнее из этих чисел в первой половине списка?
A) 1234567 Б) 3765421 В) 4123567 Г) 4352617 Д) 4376521
29
Пусть M – середина стороны BC треугольника ABC, у которого АВ = 6 см, АС = 8 см, ВС = 10 см. Пусть сторона AC пересекает сторону МD квадрата AMDE в точке F (см. рис.). Найдите (в см2) площадь четырёхугольника AFDE.
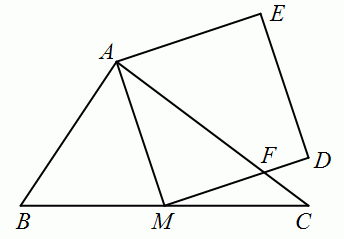
A) 124/8 Б) 125/8 В) 126/8 Г) 127/8 Д) 128/8
30
2014 солдат стоят в ряд. Каждый солдат либо всегда врёт, либо всегда говорит правду. Каждый из них заявил: «Слева от меня лжецов стоит больше, чем правдивых справа». Сколько всего лжецов стоит в этом ряду?
A) 0 Б) 1 В) 1007 Г) 1008 Д) 2014