1
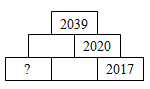
На диаграмме каждое число в верхнем и среднем ряду равно сумме двух соседних нижестоящих чисел. Какое число должно быть в ячейке, отмеченной знаком «?»?
A) 15 Б) 16 В) 17 Г) 18 Д) 19
2

Петя написал слово KANGAROO на куске прозрачного стекла (см. рис.). Что он увидит, если перевернёт этот кусок стекла через правую сторону и повернёт его на пол-оборота?

3

Анжела сделала декорацию из четырёх серых и белых кругов, наклеив их друг на друга (см. рис.). Площади кругов равны 1 см2, 4 см2, 9 см2 и 16 см2. Чему равна площадь серой части декорации?
A) 9 см2
Б) 10 см2
В) 11 см2
Г) 12 см2
Д) 13 см2
4
У Миши есть 24 рубля, а у его троих братьев – по 12 рублей. Сколько рублей Мише нужно дать каждому из своих братьев, чтобы у всех четырёх мальчиков денег стало поровну?
A) 1 Б) 2 В) 3 Г) 4 Д) 6
5
На каком из следующих рисунков показана правильная траектория движения центра колеса при его движении по зигзагообразной поверхности?

6
Несколько девушек стоят по кругу. Аня стоит пятой слева от Вали, она же стоит восьмой справа от Вали. Сколько девушек стоит по кругу?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
7
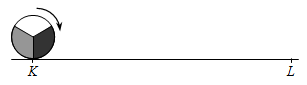
Круг радиуса 1 катится по прямой от точки K до точки L, где KL = 11π. Как будет расположено это колесо, оказавшись на точке L?

8
Мартин играет в шахматы. В этом сезоне он уже сыграл 15 партий, 9 из которых выиграл. Ему еще осталось сыграть 5 партий. Каков будет его рейтинг успеха (процент выигрышей), если все оставшиеся партии он выиграет?
A) 60% Б) 65% В) 70% Г) 75% Д) 80%
9
На свадьбе восьмую часть присутствующих составили дети. Три седьмых от числа взрослых были мужчинами. Какую часть от числа всех присутствующих составили женщины?
A) 1/2 Б) 1/3 В) 1/5 Г) 3/7 Д) 4/7
10
У моей учительницы математики есть коробка с цветными пуговицами. В ней 203 красных пуговицы, 117 белых пуговиц и 28 синих пуговиц. Сколько пуговиц нужно взять из коробки не глядя, чтобы наверняка среди них оказалось по крайней мере 3 пуговицы одного цвета?
A) 3 Б) 6 В) 7 Г) 28 Д) 203
11
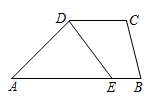
В трапеции ABCD основания равны AB = 50 см, CD = 20 см. На стороне AB выбрана точка E так, что отрезок DE делит трапецию на две части одинаковой площади. Найдите длину AE.
A) 25 см Б) 30 см В) 35 см Г) 40 см Д) 45 см
12
Сколько существует натуральных чисел a, обладающих следующим свойством: ровно одно из чисел a и a+20 является четырёхзначным?
A) 19 Б) 20 В) 38 Г) 39 Д) 40
13
В правильном треугольнике из середин сторон проведены 6 перпендикуляров к другим сторонам (см. рис.). Какую часть от площади данного треугольника составляет площадь его серой части?
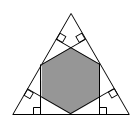
A) 1/3 Б) 2/5 В) 4/9 Г) 1/2 Д) 2/3
14
Сумма квадратов трёх последовательных натуральных чисел равна 770. Чему равно наибольшее из этих трёх чисел?
A) 15 Б) 16 В) 17 Г) 18 Д) 19
15
Система ременного привода состоит из колес A, B и C, которые вращаются без проскальзывания. Колесо B делает 4 полных оборота, если колесо A делает 5 полных оборотов. А колесо C делает 7 полных оборотов, если колесо B делает 6 полных оборотов. Чему равен периметр колеса A, если периметр колеса C равен 30 см.
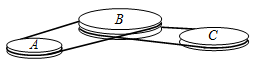
A) 27 см Б) 28 см В) 29 см Г) 30 см Д) 31 см
16
Вася занимается спортом и составляет график пробежек. Он хочет бегать ровно три раза в неделю в одни и те же дни недели, но так, чтобы не случалось пробежек два дня подряд. Сколько таких различных графиков существует?
A) 6 Б) 7 В) 9 Г) 10 Д) 35
17
У четырёх братьев разный рост. Толя ниже Володи на столько же сантиметров, на сколько он выше Пети. На такое же число сантиметров Оскар ниже Пети. Рост Толи составляет 184 см, а средний рост всех четырёх братьев равен 178 см. Каков рост Оскара?
A) 160 см Б) 166 см В) 172 см Г) 184 см Д) 190 см
18
В течение каникул 7 раз шёл дождь. Если дождь шёл утром, то днём было солнечно. А если дождь шёл днём, то утром было солнечно. Всего за каникулы утром было солнечно 5 раз, а днём – 6 раз. Сколько дней длились каникулы?
A) 7 Б) 8 В) 9 Г) 10 Д) 11
19

Жанна решила вписать в клетки таблицы 3×3 числа так, чтобы суммы чисел во всех четырёх квадратах 2×2 были одинаковыми. Три числа в угловые клетки она уже вписала так, как показано на рисунке. Какое число она должна вписать в четвёртую угловую клетку, отмеченную знаком «?»?
A) 5
Б) 4
В) 1
Г) 0
Д) невозможно определить
20
Семь натуральных чисел a, b, c, d, e, f, g выписаны в ряд. Любые два соседних числа отличаются на ±1, а сумма всех семи чисел равна 2017. Какое из чисел может равняться 286?
A) только a или g
Б) только b или f
В) только c или e
Г) только d
Д) ни одно
21
Возраст каждого из четырёх мальчиков выражается целым числом лет, меньшим 18. Ни у каких двух из них возрасты не совпадают. Произведение возрастов всех четырёх мальчиков равно 882. Чему равна сумма их возрастов?
A) 23 Б) 25 В) 27 Г) 31 Д) 33
22
В следующих пяти коробках находятся синие и красные шары, как указывают надписи. Из какой коробки вероятность достать наугад синий шар является наибольшей?

23
Двузначное число состоит из двух различных цифр a и b. Если записать это число 3 раза подряд, то получится 6-значное число, которое наверняка делится на…
A) 2 Б) 5 В) 7 Г) 9 Д) 11
24
Мой друг решил придумать пароль, состоящий из 7 цифр. Каждая цифра в пароле должна присутствовать столько раз, каково её значение. Одинаковые цифры должны быть записаны последовательно. Например, этим условиям удовлетворяют пароли 4444333, 1666666. Сколько таких различных паролей существует?
A) 6 Б) 7 В) 10 Г) 12 Д) 13
25

Павел хочет вписать натуральные числа в ячейки на рисунке так, чтобы, начиная со второго снизу ряда, каждое число являлось суммой двух чисел в соседних ячейках, расположенных непосредственно снизу от него. Какое наибольшее количество нечётных чисел может вписать Павел?
A) 13 Б) 14 В) 15 Г) 16 Д) 17
26
Лиза вычислила сумму углов выпуклого многоугольника. Но один угол она пропустила, и у нее получилось 2017°. Чему равна величина пропущенного угла?
A) 37° Б) 53° В) 97° Г) 127° Д) 143°
27
30 солдат-новобранцев стоят по кругу лицом к центру. По команде «налево» некоторые солдаты повернулись налево, а остальные – направо. Те солдаты, которые оказались лицом друг к другу, сказали «привет». Таких солдат оказалось 10. Затем по команде «кругом» все солдаты повернулись на пол-оборота. Снова, те из них, которые оказались лицом друг к другу, сказали «привет». Сколько солдат сказали привет во второй раз?
A) 10
Б) 20
В) 8
Г) 15
Д) невозможно определить
28
Толя хочет расположить на чашах весов по три гири так, чтобы правая чаша перевесила и чтобы самая тяжёлая гиря оказалась на правой чаше. Массы всех шести гирь равны 101, 102, 103, 104, 105 и 106 граммов. Сколько различных способов так расположить гири существует?
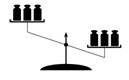
A) 6 Б) 8 В) 10 Г) 12 Д) 16
29
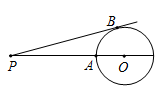
Точки A и B лежат на окружности с центром O. Прямая PB касается данной окружности в точке B. Длины отрезков PA и OB выражаются целыми числами, причём PB = PA + 6. Сколько различных значений может иметь длина OB?
A) 0 Б) 2 В) 4 Г) 6 Д) 8
30
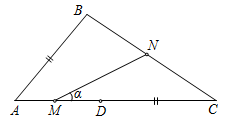
На стороне AC треугольника ABC выбрана точка D, такая, что DC = AB. Точки M и N – середины отрезков AD и BC соответственно. Если то ∠NMC = α, то ∠BAC = …
A) 2α
Б) 90° - α
В) 45° + α
Г) 90° - α/2
Д) 60°