1
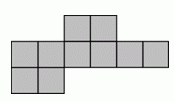
Фигура на рисунке состоит из клеток со стороной 1 см. Чему равен её периметр?
A) 14 см Б) 18 см В) 30 см Г) 32 см Д) 40 см
2
Если значения следующих выражений расположить в порядке возрастания, то какое будет средним?
A) 1 + 2345
Б) 12 + 345
В) 123 + 45
Г) 1234 + 5
Д) 12345
3
Чему равна сумма двух последних цифр произведения
1 • 2 • 3 • 4 • 5 • 4 • 3 • 2 • 1?
A) 2 Б) 4 В) 6 Г) 8 Д) 16
4
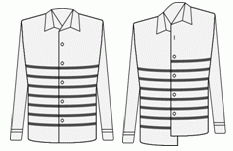
Когда Коля надевает свою новую рубашку правильно, как показано на левом рисунке, то горизонтальные полосы образуют семь замкнутых колец вокруг его талии. Этим утром он неправильно застегнул пуговицы, как показано на правом рисунке. Сколько замкнутых колец получилось вокруг талии Коли в этот раз?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
5
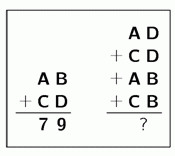
В приведённых вычислениях одинаковые буквы обозначают одинаковые цифры, а разные буквы – разные числа. Сумма двух чисел справа равна 79. Чему равна сумма четырёх чисел?
A) 79 Б) 158 В) 869 Г) 1418 Д) 7979
6
Сумма четырёх последовательных целых чисел равна 2. Чему равно наименьшее из этих чисел?
A) -3 Б) -2 В) -1 Г) 0 Д) 1
7
Годы 2020 и 1717 состоят из двух повторяющихся двухзначных чисел. Через какое наименьшее число лет после 2020 года наступит год с таким же свойством?
A) 20 Б) 101 В) 120 Г) 121 Д) 202
8
У Мэри было несколько бумажных фигур: некоторые из них – квадраты, а остальные – треугольники. Она разрезала 3 квадрата по диагонали, и у неё получилось 13 фигур, имеющих 42 вершины. Сколько треугольников выло у Мэри до того, как она сделала разрезы?
A) 8 Б) 7 В) 6 Г) 5 Д) 4
9
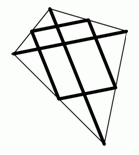
Мартин изготовил воздушного змея (см. рис.). Для этого он взял прямую деревянную планку и разрезал её на 6 частей. Две из них, длины 120 см и 80 см, он использовал как диагонали. Остальными четырьмя частями он соединил середины стороны воздушного змея. Какой длины была планка до того, как её разрезали?
A) 300 см Б) 370 см В) 400 см Г) 410 см Д) 450 см
10

На клетчатой бумаге со стороной клетки 1 отмечены четыре точки, как показано на рисунке. Какую наименьшую площадь может иметь треугольник с вершинами в каких-то трёх из отмеченных точек?
A) 1/2 Б) 1 В) 3/2 Г) 2 Д) 5/2
11
Елена хочет провести 18 дней подряд в гостях у бабушки. Её бабушка рассказывает ей интересные истории по вторникам, субботам и воскресеньям. Елена хочет услышать как можно больше бабушкиных историй. В какой день недели ей для этого нужно приехать?
A) в понедельник
Б) во вторник
В) в пятницу
Г) в субботу
Д) в воскресенье
12
Целые числа a, b, c и d удовлетворяют равенству ab = 2cd. Какое из следующих чисел не может быть значением произведения abcd ?
A) 50 Б) 100 В) 200 Г) 450 Д) 800
13
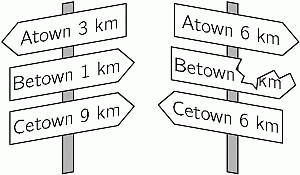
Кратчайший путь от Атауна до Цетауна пролегает через Бетаун. На этом пути сначала встречается левый указатель, а затем – правый (см. рис.). Какое расстояние было написано на сломанном знаке?
A) 1 км Б) 2 км В) 3 км Г) 4 км Д) 5 км
14
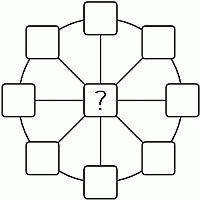
Том вписывает числа во все девять ячеек на рисунке. Он хочет, чтобы суммы трёх чисел на каждом диаметре были равны 13, а сумма всех восьми чисел на окружности равнялась 40. Какое число Том должен вписать в центральную ячейку?
A) 3 Б) 5 В) 8 Г) 10 Д) 12
15
Одна из сторон равнобедренного треугольника имеет длину 20 см. Длины двух других сторон относятся как 2 : 5. Какой периметр имеет этот треугольник?
A) 36 см Б) 48 см В) 60 см Г) 90 см Д) 120 см
16
Маша поставила знак умножения между 2-й и 3-й цифрами числа 2020 и заметила, что полученное произведение 20 • 20 является полным квадратом. Сколько всего чисел от 2010 до 2099 обладают таким же свойством?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
17
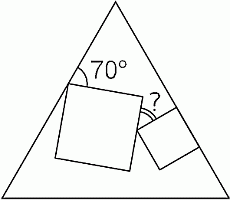
Внутри равностороннего треугольника находятся два квадрата разного размера. Одна из сторон меньшего квадрата лежит на одной из сторон треугольника, как показано на рисунке. Чему равна величина угла, отмеченного знаком вопроса?
A) 25° Б) 30° В) 35° Г) 45° Д) 50°
18
Макар отправился в 520-километровую поездку. В топливном баке ёмкостью 40 литров было 14 литров топлива. Автомобиль Макара потребляет 1 литр топлива на 10 км. Проехав 55 км, Макар увидел дорожный знак, показывающий расстояния до ближайших автозаправочных станций впереди по дороге. Эти расстояния равны 35 км, 45 км, 55 км, 75 км и 95 км. Макар хочет только один раз остановиться для дозаправки. На каком расстоянии находится нужная автозаправочная станция?
A) 35 км Б) 45 км В) 55 км Г) 75 км Д) 95 км
19
Если 17x + 51y = 102, то чему равно значение 9x + 27y?
A) 54 Б) 36 В) 34 Г) 18 Д) невозможно определить
20
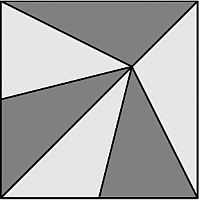
Витраж квадратной формы площади 81 дм2 состоит из шести равновеликих треугольников (см. рис.). В общей вершине всех этих треугольников сидит муха. На какой высоте от нижнего края витража она находится?
A) 3 дм Б) 5 дм В) 5,5 дм Г) 6 дм Д) 7,5 дм
21
Цифры от 1 до 9 располагаются случайным образом, образуя 9-значное число. Какова вероятность того, что полученное число делится на 18?
A) 1/2 Б) 4/9 В) 5/9 Г) 1/3 Д) 3/4
22
Заяц и Черепаха соревновались в гонке на 5 км по прямой. Скорость Зайца в 5 раз больше скорости Черепахи. Они стартовали одновременно, но Заяц по ошибке побежал перпендикулярно нужному направлению. Через некоторое время он понял свою ошибку, повернул и побежал по прямой к финишу. В результате он прибыл к финишу одновременно с Черепахой. Каково расстояние между точкой поворота Зайца и точкой финиша?
A) 11 км Б) 12 км В) 13 км Г) 14 км Д) 15 км
23
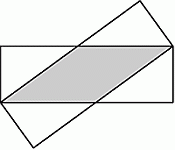
Два одинаковых прямоугольника со сторонами 3 см и 9 см расположены так, как показано на рисунке. Чему равна площадь фигуры, по которой они перекрываются?
A) 12 см2 Б) 13,5 см2 В) 14 см2 Г) 15 см2 Д) 16 см2
24
На столе находятся несколько квадратов и треугольников. Некоторые из них синие, а остальные красные. Некоторые из этих фигур большие, а остальные маленькие. Известно, что справедливы следующие два утверждения:
1) если фигура большая, то это квадрат:
2) если цвет фигуры синий, то это треугольник.
Какое из следующих утверждений верно?
A) все красные фигуры являются квадратами
Б) все квадраты большие
В) все маленькие фигуры синие
Г) все треугольники синие
Д) все синие фигуры маленькие
25
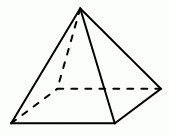
Кенга пронумеровал вершины четырёхугольной пирамиды числами 1, 2, 3, 4 и 5. Затем для каждой грани Кенга вычислил сумму чисел в вершинах данной грани. Четыре из этих сумм оказались равны 7, 8, 9 и 10. Чему равна сумма чисел в вершинах пятой грани?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
26
Большой куб построен из 64 меньших одинаковых кубиков. Три из граней большого куба окрасили. Какое наибольшее количество маленьких кубиков может иметь ровно одну окрашенную грань?
A) 27 Б) 28 В) 32 Г) 34 Д) 40
27
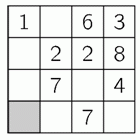
Аня хочет вписать числа во все клетки квадрата 4 × 4 так, чтобы суммы чисел во всех строчках и всех столбцах были одинаковыми. Несколько чисел она уже вписала, как показано на рисунке. Какое число она должна будет вписать в серую клетку?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
28
Алиса, Белла и Виктория устроили соревнование по армрестлингу. В каждом поединке боролись две девушки, в то время как третья отдыхала. После каждого поединка победительница продолжала борьбу с той девушкой, которая отдыхала. Известно, что Алиса участвовала в 10 поединках, Белла – в 15, а Виктория – в 17. Кто проиграл во втором поединке?
A) Алиса
Б) Белла
В) Виктория
Г) Алиса или Белла
Д) Алиса или Виктория
29
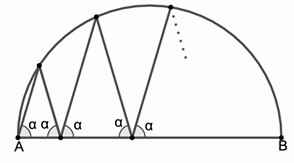
Ломаная вписана в полукруг. Она начинается в точке A диаметра AB и заканчивается в точке B (см. рис.). Внутри дуги полукруга ломаная имеет 4 вершины. Все углы между отрезками ломаной и диаметром AB равны α. Чему равен угол α?
A) 60° Б) 72° В) 75° Г) 80° Д) другой ответ
30
Восемь последовательных трёхзначных натуральных чисел имеют следующее свойство: каждое из них делится на его последнюю цифру. Какова сумма цифр наименьшего из этих восьми целых чисел?
A) 10 Б) 11 В) 12 Г) 13 Д) 14