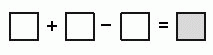Задание 1
|
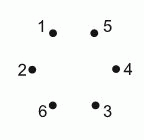
Шесть точек пронумерованы, как показано на рисунке. Сначала Кристина соединила отрезками точки с чётными номерами и получила один треугольник. Затем она соединила отрезками точки с нечётными номерами и получила другой треугольник. Один треугольник она окрасила в чёрный цвет, а другой – в серый. В каком из следующих ответов изображены построенные Кристиной треугольники?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Чётными числами на рисунке в условии задачи являются числа 2, 4 и 6. Соединив отрезками соответствующие точки, получим треугольник, который имеется только в ответе Д. Нечётными являются числа 1, 5 и 3. Соединив отрезками соответствующие им
точки, получим треугольник, который также имеется только в ответе Д.
Задание 2
|
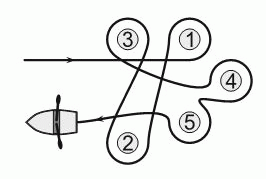
Лена проплыла на лодке вокруг пяти буёв, как показано на рисунке. Какие буи она огибала против хода часовой стрелки?
A) 1 и 4
Б) 2, 3 и 5
В) 2 и 3
Г) 1, 4 и 5
Д) 1 и 3
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33 + 3 = 36
|
На следующем рисунке стрелками показано, в каком направлении огибались буи. Видим, что против хода часовой
стрелки лодка огибала буи 1 и 3.

Задание 3
|
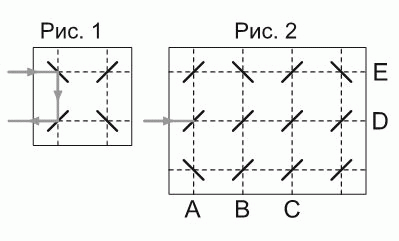
Луч лазера отражается от зеркал так, как показано на рисунке 1. В какой точке выйдет луч лазера на втором рисунке 2?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 36 + 3 = 39
|
На следующем рисунке показан путь луча. Видим, что он выходит из системы зеркал в точке В.

Задание 4
|
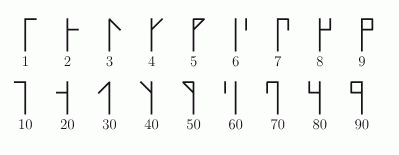
Цистерцианские цифры использовались в начале тринадцатого века. Любое целое число от 1 до 99 может быть представлено одним глифом, образованным путем соединения двух глифов. Например, 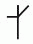 ,
, 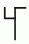 и
и  – это соответственно 24, 81 и 93. Какой глиф представляет число 45?
– это соответственно 24, 81 и 93. Какой глиф представляет число 45?
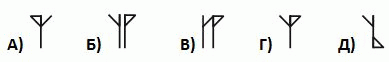
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 39 + 3 = 42
|
Соединив глифы 40 и 5, т.е.  , получим глиф
, получим глиф  . Таким образом, правильным является ответ Г.
. Таким образом, правильным является ответ Г.
Задание 5
|
Шарики продаются в пакетах по 5, 10 или 25 штук. Том купил ровно 95 шариков. Какое наименьшее количество пакетов, он мог купить?
A) 4 Б) 5 В) 7 Г) 8 Д) 10
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 42 + 3 = 45
|
Чтобы число пакетов было наименьшим, нужно купить как можно больше пакетов с наибольшим количеством шариков. Пакетов с 25 шариками не может быть больше 3, иначе число купленных шариков будет не меньше 25 · 4 = 100. Если взять 3 пакета с 25 шариками, то в них будет 25 · 3 = 75 шариков и понадобятся ещё 95 – 75 = 20 шариков. Для их покупки понадобятся ещё по крайне мере 2 пакета с 10 шариками. Таким образом, наименьшее число пакетов равно 3 + 2 = 5. Тем самым, правильным является ответ Б.
Задание 6
|
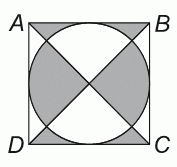
Сторона квадрата ABCD равна 10 см. Чему равна площадь серой части этого квадрата?
A) 40 см2 Б) 45 см2 В) 50 см2 Г) 55 см2 Д) 60 см2
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 45 - 0.75 = 44.25
|
Площадь всего данного квадрата равна 10 · 10 = 100 см2. Серые участки составляют ровно половину площади квадрата (см. рис.). Действительно, если согнуть квадрат по диагонали, то все серые участки в точности совместятся с белыми и, наоборот, все белые участки совместятся с серыми. Следовательно, серая часть квадрата равна его белой части и, значит, равна 100 : 2 = 50 см2.
Задание 7
|
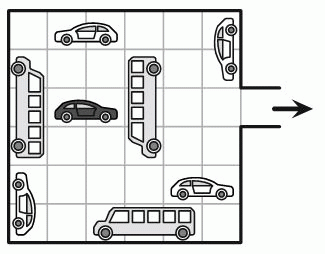
В гараже на рисунке автомобили могут двигаться только вперёд или назад, но не могут поворачивать. Какое наименьшее количество автомобилей должно переместиться, чтобы чёрный автомобиль мог выехать из гаража?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 44.25 + 3 = 47.25
|

Для того чтобы чёрный автомобиль смог выехать из гаража, необходимо освободить клетку А. Для этого соответствующий автомобиль должен отъехать на 2 клетки. Он не может отъехать на две клетки назад. Чтобы он смог проехать
на 2 клетки вперёд, необходимо, чтобы освободилась клетка В. Для этого автомобиль, занимающий эту клетку,
также должен отъехать на 2 клетки. Снова, этот автомобиль может проехать на 2 клетки только вперёд. Но это возможно только при условии, что освободится клетка С. Для этого, в свою очередь, должна освободиться клетка D. Видим, что переместиться должны по крайней мере 4 автомобиля. Если автомобили сначала D, а затем C проедут
вперёд на 1 клетку, после этого сначала B, а затем A – на 2 клетки вперёд, то у чёрного автомобиля не будет препятствий для выезда из гаража.
Задание 8
|
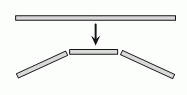
Юля хочет приготовить спагетти. У неё есть одна длинная нить спагетти, которую ей нужно разломать. Первый раз она ломает её на 3 части. Далее некоторые из образовавшихся кусков она каждый раз также ломает на 3 части. Какое из следующих чисел НЕ МОЖЕТ быть числом кусков, которые в результате могли получиться у Юли?
A) 13 Б) 17 В) 20 Г) 23 Д) 25
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 47.25 + 3 = 50.25
|
После первого разлома нити спагетти на 3 куска и после всех последующих разломов число кусков увеличивается на 2. (Один кусок исчезает и три новых появляются.) Поэтому, так как вначале был 1 кусок (а 1 – нечётное число), после каждого разлома число кусков будет оставаться нечётным. Во всех вариантах ответа, кроме В, указаны нечётные числа. Все нечётные числа кусков могли получиться. А 20 кусков получиться не могло.
Задание 9
|

Боря сложил в некотором порядке следующие 7 плиток с числами так, что у него получилось 12-значное число. Какими тремя цифрами заканчивается наименьшее из чисел, которые могли получиться у Бори?
A) 699 Б) 113 В) 551 Г) 967 Д) 459
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 50.25 - 0.75 = 49.5
|
Чтобы число из некоторого набора цифр было наименьшим, необходимо, чтобы на старшие разряды приходились как можно меньшие цифры, т.е. цифры (слева направо) должны располагаться в порядке неубывания. Но в данном случае не на всех карточках изображены цифры. На четырёх карточках записаны многозначные числа. Цифры на них нельзя поменять местами, тем более, использовать отдельно. Поэтому, чтобы составить из карточек наименьшее число, нужно расположить карточки в порядке неубывания первых цифр на этих карточках. В случае совпадения первых цифр, такое же правило следует применить для вторых цифр и т.д. Поэтому данные карточки нужно расположить так: 113, 4, 51, 5, 67, 69, 9. Видим, что полученное наименьшее число будет заканчиваться цифрами 699.
Задание 10
|
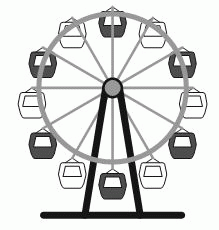
На какую наименьшую часть оборота должно повернуться колесо обозрения, чтобы наверху оказалась белая кабинка?
A) 1/2 Б) 1/3 В) 1/6 Г) 1/12 Д) 5/6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 49.5 + 3 = 52.5
|
Соседними с верхней чёрной кабинкой являются белые кабинки. Поэтому наименьшим будет поворот, если одна из
них займёт место верхней чёрной кабинки. Всего на колесе обозрения имеется 12 кабинок. Поэтому кабинки занимают место соседних при повороте колеса на 1/12 оборота.
Задание 11
|
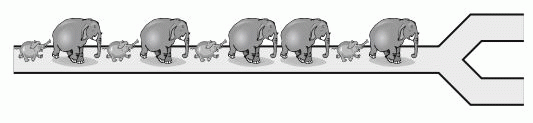
Пять слонов и четыре слонёнка идут друг за другом по тропинке, как показано на рисунке. На развилке каждый из них поворачивает либо налево, либо направо. В какой последовательности они НЕ МОГУТ идти после развилки?
A) 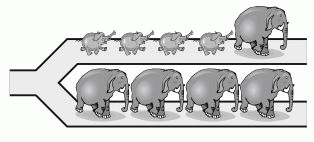
Б) 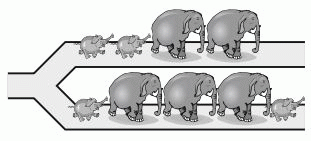
В) 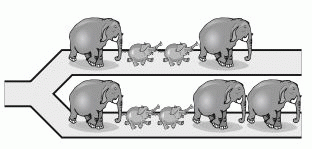
Г) 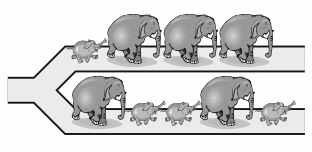
Д) 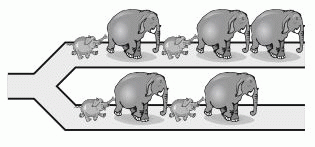
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 52.5 + 4 = 56.5
|
Заметим, что последним в данной цепочке животных является слонёнок.
После развилки он также будет последним.
Видим, что последовательность в ответе В невозможна. Можно убедиться, что разойтись на развилке так, как показано в других вариантах ответа, животные могли.
Задание 12
|
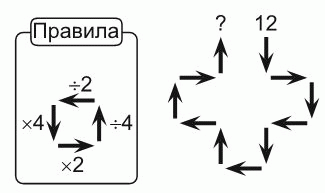
Клара начала с числа 12 и, продвигаясь по стрелкам, преобразует его согласно правилам. Что у неё получится в результате?
A) 13 Б) 6 В) 12 Г) 24 Д) 48
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 56.5 + 4 = 60.5
|
Чтобы найти правильный ответ, совсем не обязательно выполнять все преобразования на указанном пути. Заметим, что количество стрелок вверх такое же, как и вниз (см. рис.). Поэтому сколько раз текущее значение будет умножаться на 4, столько же раз оно будет делиться на 4. В совокупности, поскольку порядок операций умножения и деления неважен (результат не меняется при их перестановке), они исходное число не изменят.
Что касается горизонтальных стрелок, то стрелок влево на одну больше, чем вправо. Поэтому операций деления на 2 будет на одну больше, чем операций умножения на 2, и в результате у Клары получится число 12 : 2 = 6.
Задание 13
|
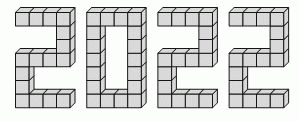
Миша и его друзья склеили число 2022 из 66 кубиков, как показано на рисунке. Они окрасили поверхности всех получившихся цифр в серый цвет. У какого числа кубиков оказались окрашены ровно 4 грани?
A) 16 Б) 30 В) 46 Г) 54 Д) 60
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 60.5 + 4 = 64.5
|
Крайние кубики цифры 2 склеены только с одним кубиком. Поэтому у них окрашены 5 граней из шести. Три цифры 2 имеют 6 таких кубиков. Все остальные кубики склеены ровно с
двумя другими кубиками. Поэтому у них ровно 4 грани окрашены. Так как всего было использовано 66 кубиков, то искомое число кубиков равно 66 – 6 = 60.
Задание 14
|
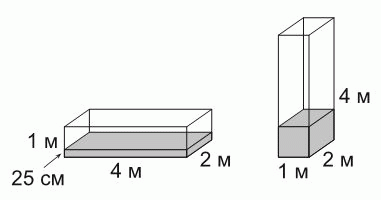
Резервуар для воды прямоугольной формы имеет размеры 1м x 2м x 4м. На первом рисунке уровень воды в резервуаре равен 25 см. Каков уровень такого же объёма воды в этом резервуаре на втором рисунке?
A) 25 см Б) 50 см В) 75 см Г) 1 м Д) 1,25 м
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 64.5
Согласно данным на первом рисунке в условии задачи, объём жидкости в резервуаре равен 4 · 2 · 0,25 = 2 м3. На втором рисунке – тот же резервуар с тем же объёмом жидкости. Но на этот раз площадь его основания равна 1 · 2 = 2 м2. Поэтому уровень
жидкости равен 2 : 2 = 1 м.
По-другому правильный ответ можно получить так. Согласно данным на первом рисунке в условии, жидкость занимает четвёртую часть от объёма всего резервуара. Поэтому на втором рисунке (как и на первом) уровень жидкости тоже составляет четвёртую часть высоты резервуара. А так как высота резервуара на втором рисунке равна 4 м, то уровень жидкости равен 4 : 4 = 1 м.
|
Задание 15
|
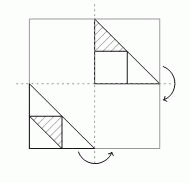
На рисунке показан прозрачный лист бумаги с рисунком на нём. Лист согнули дважды так, как показано на рисунке. Как он может выглядеть после этого?

|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 64.5 - 1 = 63.5
|
На следующем рисунке показаны результаты первого и второго сворачиваний данного листа. Видим, что получится результат, указанный в ответе А.

Задание 16
|
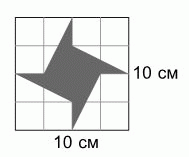
Площадь квадрата на рисунке равна 100 см2. Какую площадь имеет его окрашенная часть?
A) 20 см2 Б) 25 см2 В) 30 см2 Г) 35 см2 Д) 40 см2
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 63.5 + 4 = 67.5
|
Прорисуем полностью стороны всех клеток.

Видим, что, помимо клеток, образуются 8 равных треугольников. Половина из них окрашена, а половина не окрашена. Поэтому, если убрать окраску у окрашенных треугольников и окрасить неокрашенные треугольники, то, во-первых, площадь окрашенной части не изменится, а во-вторых, окрашенными окажутся ровно 4 из 16 клеток. Следовательно, площадь окрашенной части в 16 : 4 = 4 раза меньше площади данного квадрата и, значит, равна 100 : 4 = 25 см2.
Задание 17
|
Для черепахи Евы 2022 год уже третий со дня её рождения, в записи которого есть три одинаковые цифры. Какое наименьшее число лет может быть Еве к концу этого года?
A) 18 Б) 20 В) 22 Г) 23 Д) 134
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 67.5 - 1 = 66.5
|
Два числа с тремя одинаковыми цифрами, непосредственно предшествующие числу 2022, – это 2000 и 1999. Поэтому черепаха Ева родилась не позже 1999 года и, значит, к концу 2022 года ей будет не менее 2022 – 1999 = 23 лет.
Задание 18
|
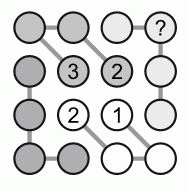
Андрей хочет заполнить пустые кружочки таблицы так, чтобы в каждой строке, каждом столбце и каждой четвёрке кружочков, соединенных отрезками, были числа 1, 2, 3 и 4. Какое число он должен записать в кружке со знаком вопроса?
A) 1 Б) 2 В) 3 Г) 4 Д) невозможно определить
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 66.5 + 4 = 70.5
|
В верхней строчке первые два кружочка входят в четвёрку, в которой уже имеются числа 2 и 3 (см. рис.). Поэтому первые два числа в верхней строчке – это 1 и 4 (или 4 и 1). Тогда последние два числа в этой строчке – это 2 и 3, в каком-то порядке. Но число 2 не может быть третьим в данной строчке, иначе в третьем столбце таблицы будут два числа 2 и условия задачи для этого столбца не будут выполнены. Следовательно, в верхней строчке третье число – это число 3, а последнее (искомое) – это число 2.
Заметим, что найденное значение искомого числа не гарантирует, что требуемое заполнение таблицы существует. Для убедительности построим пример.

Задание 19
|
У Лизы есть 4 собаки. Каждая из них весит целое число килограммов. Вместе все они весят 60 кг. Все собаки разные по весу. Вторая по весу (в порядке убывания) собака весит 28 кг. Сколько весит третья (в порядке убывания веса) собака?
A) 2 кг Б) 3 кг В) 4 кг Г) 5 кг Д) 6 кг
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 70.5 + 4 = 74.5
|
Если бы третья по весу собака весила 3 или более килограммов, то вес всех собак был бы не менее 29 + 28 + 3 + 1 = 61 кг, что противоречит условию задачи. Далее, четвёртая по весу (самая лёгкая) собака весит не менее 1 кг. Получаем единственную возможность: третья по весу собака весит 2 кг. Таким образом, правильным является ответ 2 кг. Тогда, действительно, все четыре собаки весят 29 + 28 + 2 + 1 = 60 кг.
По-другому найти правильный ответ можно так. Заметим, что самая тяжёлая собака может весить только 29 кг. Действительно, в противном случае все собаки весили бы не менее 30 + 28 + 2 + 1 = 61, противоречие. Итак, две самые тяжёлые собаки весят 29 + 28 = 57 кг. Поэтому две самые лёгкие собаки весят 60 – 57 = 3 кг.
Это возможно, только если их вес 2 кг и 1 кг. Видим, что третья по весу собака весит 2 кг.
Задание 20
|
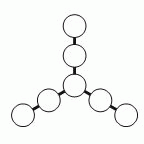
Алеся хочет вписать в кружочки на рисунке числа 3, 4, 5, 6, 7, 8 и 9 так, чтобы суммы всех троек чисел, расположенных на одной прямой, были одинаковыми. Какое наибольшее значение может иметь сумма чисел одной такой тройки чисел?
A) 28 Б) 18 В) 22 Г) 16 Д) 20
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 74.5 + 4 = 78.5
|
Сумма чисел в каждой тройке будет наибольшей, если сумма сумм троек будет
наибольшей. Число в центре входит во все тройки, остальные числа – только в одну тройку. Поэтому сумма чисел во всех тройках будет наибольшей, если центральное число будет наибольшим. Наибольшее среди данных чисел – число 9. Чтобы получить соответствующий пример, достаточно разбить остальные числа (3, 4, 5, 6, 7, 8) на пары с одинаковыми суммами. Такое разбиение легко получить: 3 + 8 = 11, 4 + 7 = 11, 5 + 6 = 11. Следовательно, наибольшее значение суммы одной тройки равно 11 + 9 = 20.

Задание 21
|
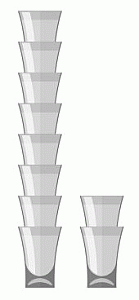
Стаканы вставляют друг в друга (см. рис.). Стопка из 8 стаканов имеет высоту 42 см, а стопка из 2 стаканов – 18 см. Какую высоту имеет стопка из 6 стаканов?
A) 22 см Б) 24 см В) 38 см Г) 34 см Д) 40 см
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 78.5 + 5 = 83.5
|
Из условия задачи следует, что при увеличении стопки на 8 – 2 = 6 стаканов её высота увеличивается на 42 – 18 = 24 см. Тогда при увеличении стопки на 2 стакана, т.е. в 3 раза меньше, высота увеличивается на 24 : 3 = 8 см. Поэтому стопка из 6 стаканов имеет высоту 18 + 8 + 8 = 34 см.
Задание 22
|
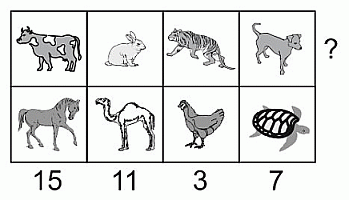
Каждое животное в таблице представляет некоторое натуральное число, разные животные – разные числа. Суммы чисел в столбцах указаны под соответствующими столбцами. Какое наибольшее значение может иметь сумма чисел в первой строке таблицы?
A) 18 Б) 19 В) 20 Г) 21 Д) 22
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 83.5 - 1.25 = 82.25
|
Все животные в таблице разные, поэтому и все соответствующие им числа различны. Сумма чисел в третьем столбце равна 3 = 2 + 1. Поэтому сумма чисел в верхней строчке
будет наибольшей, если тигр представляет число 2. Далее, сумма чисел в четвёртом столбце равна 7. Ни одно из этих чисел не может быть равно ни 2, ни 1. Тогда эти числа – 4 и 3. Поэтому наибольшее значение, представляемое собакой, – это число 4. Во втором столбце сумма двух чисел равна 11. И каждое из них больше числа 4. Значит, это числа 6 и 5. Наибольшее значение, представляемое зайцем, равно 6. Наконец, сумма двух чисел в первом столбце равна 15. Каждое из них больше числа 6. Поэтому наибольшее значение числа, представляемого коровой, равно 8. Таким образом, наибольшее значение суммы чисел в первой строке таблицы равно
8 + 6 + 2 + 4 = 20.
Задание 23
|
Определите правильный код замка по следующим подсказкам.
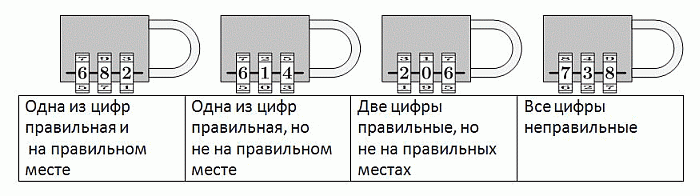
A) 604 Б) 082 В) 640 Г) 042 Д) 046
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 82.25 + 5 = 87.25
|
У первых двух подсказок (682 и 614) цифра 6 стоит на первом месте. Поэтому она не может быть правильной, так как, согласно второй подсказке, правильная цифра стоит на неправильном месте. Далее, согласно последней подсказке, код не содержит цифр 7, 3, 8. Поэтому правильной цифрой кода на правильном месте у числа 682 является цифра 2, и она стоит на правильном третьем месте. Тогда, согласно третьей подсказке (число 206 имеет 2 правильные цифры, но не на правильных местах), правильной цифрой
является цифра 0, но она должна быть на первом месте. Ещё одной
цифрой (на втором месте), как следует из второй подсказки, является цифра 4. Таким образом, правильный код замка – 042.
Задание 24
|
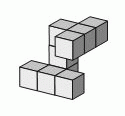
Аня склеила из кубиков фигуру на рисунке. С какой из следующих фигур она совпадает?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 87.25 + 5 = 92.25
|
Данная фигура состоит из трёх столбиков, полученных из трёх склеенных кубиков, расположенных в один ряд. У среднего столбика крайние кубики склеены со средними кубиками двух других столбиков. Среди вариантов ответа только фигуры в вариантах В и
Г обладают таким свойством. Но в варианте Г два столбика (вертикальные) расположены параллельно. У данной фигуры нет параллельных столбиков. Видим, что единственным правильным ответом может быть только ответ В. Действительно, если данную фигуру повернуть так, чтобы верхний горизонтальный столбик стал вертикальным, а затем повернуть её так, чтобы этот столбик оказался слева, то получим вид этой фигуры, указанный в ответе В.
Задание 25
|
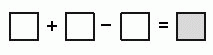
Вернер вписывает числа 2, 3, 4, 5 и 6 в клетки на рисунке так, чтобы получилось правильное равенство. Сколько из этих чисел могут быть вписаны в серую клетку?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 92.25 - 1.25 = 91
|
Каждое из данных пяти чисел может быть результатом, вписанным в серую клетку:
3 + 5 – 6 = 2,
2 + 6 – 5 = 3,
2 + 5 – 3 = 4,
2 + 6 – 3 = 5,
3 + 5 – 2 = 6.
Поэтому правильным является ответ 5.
Задание 26
|
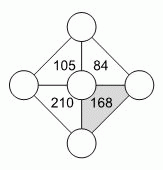
В кружочки в таблице нужно вписать числа 3, 4, 5, 6 и 7 так, чтобы произведения чисел в вершинах треугольников были такими, как указано на рисунке. Чему равна сумма чисел в вершинах окрашенного треугольника?
A) 12 Б) 14 В) 15 Г) 17 Д) 18
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 91
Разложим данные произведения на простые множители:
210 = 2 · 3 · 5 · 7,
105 = 3 · 5 · 7,
84 = 2 · 2 · 3 · 7,
168 = 2 · 2 · 2 · 3 · 5 · 7.
Видим, что все числа делятся на 7, но не все делятся на 3, 4, 5, 6. Поэтому в центре должно быть число 7. Только числа 105 и 210 делятся на 5. Поэтому слева должно быть число 5. Тогда,
чтобы получалось произведение 210, нижним должно быть число 210 : (5 · 7) = 6. Далее, чтобы получалось произведение 168, справа должно быть число 168 : (7 · 6) = 4. Тогда сумма чисел в вершинах окрашенного треугольника равна 7 + 6 + 4 = 17.

|
Задание 27
|
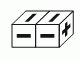
Какой из следующих развёрток НЕ МОЖЕТ быть развёртка параллелепипеда на рисунке сверху?

|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 91 - 1.25 = 89.75
|
Повернём развёртку Б на пол-оборота и свернём её так, чтобы получился параллелепипед. Повернём полученный параллелепипед так, чтобы знак «+» оказался на одноклеточной грани справа, а на передней грани знаки «–» располагались горизонтально. Получим вид параллелепипеда, указанный на следующем рисунке. (Клетки видимых граней на втором изображении развёртки выделены.)

Сравнивая результат с исходным параллелепипедом, видим, что изображения на правой клетке верхней грани не совпадают. Поэтому развёртка Б не может быть развёрткой данного параллелепипеда. Можно убедиться, что из других развёрток свернуть данный параллелепипед можно. Таким образом, правильным является ответ Б.
Задание 28
|
Четыре деревни A, B, C и D расположены вдоль дороги в указанном порядке. Расстояние между соседними деревнями равно 10 км. В деревне A живут 10 школьников, в деревне B – 20 школьников, в деревне C – 30 школьников, в деревне D – 40 школьников. Где нужно построить школу, чтобы сумма расстояний до школы у всех этих школьников была наименьшей?
A) в А
Б) в В
В) посередине между В и С
Г) в С
Д) в D
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 89.75 - 1.25 = 88.5
|
Для каждого из мест расположения школ в вариантах ответа найдём суммы расстояния до школы.

Школа в A: 20 × 10 + 30 × 20 + 40 × 30 = 2000 км.
Школа в B: 10 × 10 + 30 × 10 + 40 × 20 = 1200 км.
Школа посередине между B и C: 10 × 15 + 20 × 5 + 30 × 5 + 40 × 15 =
= 1000 км.
Школа в C: 10 × 20 + 20 × 10 + 40 × 10 = 800 км.
Школа в D: 10 × 30 + 20 × 20 + 30 × 10 = 1000 км.
Видим, что общее расстояние до школы будет наименьшим, если она
будет построена в деревне С.
Задание 29
|
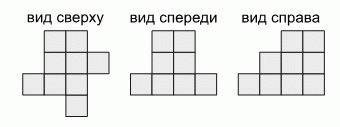
Из одинаковых кубиков построили некоторую конструкцию. На рисунке показан вид этой конструкции сверху, спереди и справа. Какое наибольшее количество кубиков могло быть использовано для построения данной конструкции?
A) 18 Б) 19 В) 20 Г) 21 Д) 22
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 88.5
Рассмотрим вид конструкции сверху и в каждой клетке укажем наибольшее количество кубиков, которые могут стоять на данной клетке. При этом будем учитывать вид спереди и вид справа (см. рис.).

В результате находим, что наибольшее возможное число кубиков равно
3 + 3 + 3 + 3 + 1 + 1 + 2 + 2 + 1 = 19.
|
Задание 30
|
За круглым столом сидят 30 человек. Некоторые из них в шляпе. Те, кто носит шляпу, всегда говорят правду, а те, кто не носит шляпу, могут лгать или говорить правду. Каждый говорит: «По крайней мере, один из двух моих соседей слева и справа не носит шляпы». Какое наибольшее число людей, сидящих за столом, может носить шляпу?
A) 5 Б) 10 В) 15 Г) 20 Д) 25
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 88.5 + 5 = 93.5
|
Рассмотрим троих подряд сидящих за столом. Все трое не могут носить шляпу. Действительно, все, кто в шляпе, – правдивые. Но тогда у среднего из них оба соседа были бы в шляпах, и он не мог бы сказать: «По крайней мере один из двух моих соседей не носит шляпы». А два среди любых трёх подряд сидящих могут носить шляпу. Соответствующая рассадка:
Ш Ш Б Ш Ш Б Ш Ш Б … Ш Ш Б
(«Ш» означает «в шляпе», «Б» означает «без шляпы»). Следовательно, наибольшее число людей за столом, которые носят шляпу, равно 20.



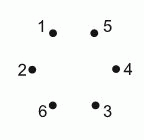






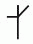 ,
, 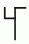 и
и  – это соответственно 24, 81 и 93. Какой глиф представляет число 45?
– это соответственно 24, 81 и 93. Какой глиф представляет число 45?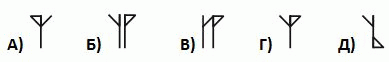
 , получим глиф
, получим глиф  . Таким образом, правильным является ответ Г.
. Таким образом, правильным является ответ Г.