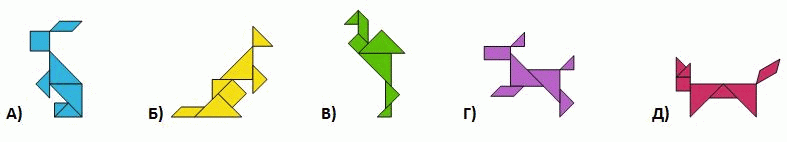Задание 1
|
На каком из следующих рисунков больше всего треугольников?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 24 + 3 = 27
|
Количество треугольников на рисунках: А - 1, Б - 4, В - 2, Г - 3, Д - 1. Видим, что больше всего треугольников на рисунке Б.
Задание 2
|
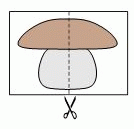
Арик разрезал следующий рисунок пополам и переложил две половинки. Что у него могло получиться?

|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 27 - 0.75 = 26.25
|
Могла получиться только картинка в ответе Д. Если на ней повернуть правую половину на пол-оборота против хода часовой стрелки, то восстановится исходный рисунок.
Задание 3
|
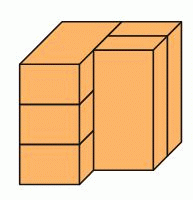
Фигура на рисунке состоит из пяти одинаковых кирпичей. Сколько из этих кирпичей касаются ровно трёх других кирпичей?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 26.25 - 0.75 = 25.5
|
Трёх других кирпичей касаются только верхний и нижний кирпичи в левой стопке. На рисунке они белого цвета. Остальные кирпичи касаются всех других, т.е. четырёх из имеющихся пяти кирпичей.
Задание 4
|
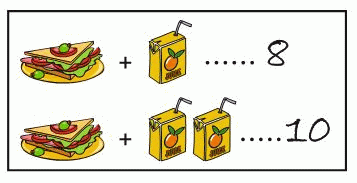
Сэндвич и сок стоят 8 рублей. Сэндвич и два сока стоят 10 рублей. Сколько стоит один сок?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 25.5
Во втором наборе на один сок больше. И второй набор, согласно условию, стоит на 10 – 8 = 2 рубля больше. Следовательно, один сок стоит 2 рубля.
|
Задание 5
|
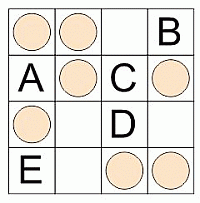
На некоторых клетках таблицы находятся монеты. На какую клетку нужно положить ещё одну монету так, чтобы в каждой строчке и в каждом столбце таблицы было ровно по 2 монеты?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 25.5
В третьей сверху строчке и третьем слева столбце находится только по одной монете. Поэтому, чтобы их стало две, нужно положить монету в указанные строчку и столбец, т.е. на их общую клетку D.
|
Задание 6
|
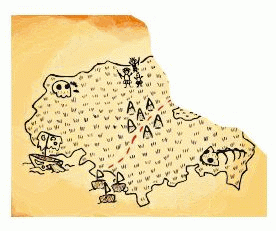
Обезьянка оторвала кусок от карты капитана Джека. Каким может быть этот кусок?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 25.5 + 3 = 28.5
|
На рисунке отсутствует кусок карты в правом верхнем углу. У верхней стороны карты не хватает приблизительно половины, а у правой стороны – более половины. Описанными размерами обладают куски Б и Д. Но на куске Д нет продолжения штрихового пути с указанием места клада. Такое продолжение есть на куске Б. Поэтому правильным является ответ Б.

Задание 7
|

Петя сложил квадрат из четырёх плиток пазла на рисунке. Какой квадрат у него получился?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 28.5 + 3 = 31.5
|
На следующем рисунке показано, как сложить плитки пазла, чтобы получился квадрат. Видим, что получится рисунок, указанный в варианте ответа Б.

Задание 8
|

На клетчатый лист бумаги разлились чернила, как показано на рисунке. Сколько клеток оказались (частично или полностью) залиты чернилами?
A) 16 Б) 17 В) 18 Г) 19 Д) 20
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 31.5 + 3 = 34.5
|
Всего на бумаге 4 · 6 = 24 клеток. Только 4 угловые клетки остались чистыми. Следовательно, залиты чернилами 24 – 4 = 20 клеток.
По-другому найти ответ можно так. Прорисуем все клетки и подсчитаем непосредственно количество тех, которые залиты чернилами (см. рис.). Их 20.

Задание 9
|

Кенгуру написал число, а затем накрыл цифры фигурками (одинаковые цифры – одинаковыми фигурками, а разные разными). Каким из следующих чисел может быть число, написанное Кенгуру?
A) 34426 Б) 34526 В) 34423 Г) 34424 Д) 32446
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 34.5 + 4 = 38.5
|
По расположению фигурок видно, что только вторая и третья цифры должны быть одинаковыми. Ещё три цифры отличны от совпадающих двух. Просматривая варианты ответа, видим, что только число А) 34426 удовлетворяет данным условиям.
Задание 10
|

В каждой из следующих корзин спит по одному зверьку. Медвежонок и лисёнок спят в корзинах одинаковой формы с одинаковым узором. У Кенгурёнка и котёнка одинаковый узор на корзинках. В какой корзине спит щенок?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 38.5 - 1 = 37.5
|
Согласно условию, медвежонок и лисёнок спят в корзинах 2 и 4 (см. рис. в условии задачи). Далее, кенгуру и котёнок
спят в корзинах 1 и 3. Итак, щенок не спит в корзинах 1, 2, 3 и 4. Значит,
он спит в корзине 5.
Задание 11
|
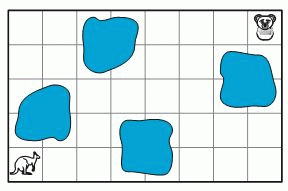
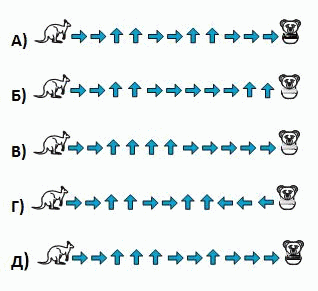
Кенгуру хочет пройти до клетки с коалой по неокрашенным клеткам. Какой путь ему следует выбрать?
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 37.5 + 4 = 41.5
|
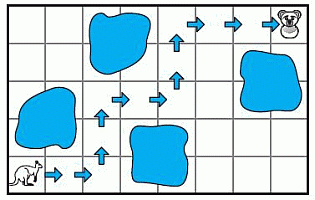
Кенгуру может начать ровно с двух прыжков вправо. Это условие имеет место во всех вариантах ответа. Затем должны последовать ровно 2 прыжка вверх. Уже видим, что ответы В и Д не являются верными. Далее, возможны 2 или 3 прыжка направо. Поэтому ответ Б неправильный. Из оставшихся двух ответов ответ Г также неправильный, потому что последний прыжок, определённо, должен быть направо. А ответ А, действительно, подходит (см. рис.).
Задание 12
|
Вася сложил 5 зверюшек из геометрических фигур. Одна из таких фигур есть только у одной зверюшки. У какой?
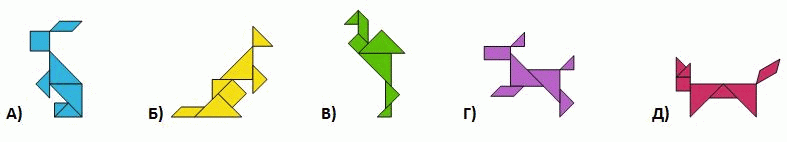
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 41.5
Прямоугольник (но не квадрат!) имеется только на рисунке Г (мордочка собачки).
|
Задание 13
|
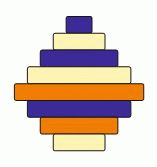
Какой вид сверху имеет следующая пирамидка, сложенная из разноцветных дисков?

|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 41.5
Просматривая диски пирамидки сверху вниз, мы сначала (в центре) увидим синий диск. Он будет окружён жёлтым кольцом. Затем идут синее кольцо, снова жёлтое кольцо и, наконец, оранжевое кольцо. Три нижних диска сверху видны не будут. Описанное чередование цветов имеется только
в ответе А.
|
Задание 14
|
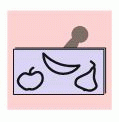
Какой отпечаток делает штамп на рисунке сверху?

|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 41.5 - 1 = 40.5
|
На отпечатке получается рисунок, симметричный тому, который имеется на штампе. Поэтому фигурки рисунка, расположенные на штампе слева направо, на отпечатке будут расположены в обратном порядке. В частности, слева будет груша, а справа – яблоко. Видим, что ответ А неверный. Далее, верхушка груши (с хвостиком) на штампе наклонена вправо. Тогда на отпечатке она будет наклонена влево. Поэтому ответы Б и В не являются верными. Заметим также, что хвостик яблока на штампе загнут вправо к центру. Тогда на отпечатке он будет загнут влево к центру. Видим, что из двух оставшихся вариантов ответа правильным является ответ Г.
Задание 15
|
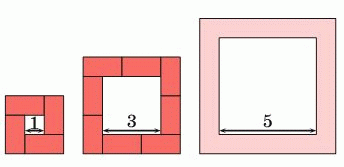
Катя строит вокруг квадратов «забор» из доминошек, состоящих из двух клеток со стороной 1, как показано на рисунке. Сколько доминошек ей понадобится, чтобы построить «забор» вокруг квадрата со стороной 5?
A) 10 Б) 11 В) 12 Г) 14 Д) 16
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 40.5
Можно непосредственно нарисовать
забор вокруг квадрата со стороной 5 и подсчитать, что он будет состоять из 12 доминошек. Но ответ можно получить и без непосредственных построений. Заметим, что при увеличении стороны квадрата на 2 каждая сторона забора по длине должна увеличиваться ровно на одну доминошку. Всего для увеличения стороны на 2 понадобятся 4 дополнительные доминошки. Так, первый забор на рисунке состоит из 4 доминошек, второй – из 8 доминошек. Тогда третий (искомый) забор будет состоять из 8 + 4 = 12 доминошек.
|
Задание 16
|
У Ани есть стикеры:

Она клеит их друг на друга. Звезду она наклеила после квадрата, но до того, как наклеила треугольник. Что у неё могло получиться в результате?

|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 40.5 - 1 = 39.5
|
Согласно условию задачи, Аня наклеила звезду до того, как она наклеила треугольник. Однако во всех вариантах ответа, кроме Д, звезда, наоборот, наклеена после треугольника. Поэтому верным может быть только ответ Д.
Задание 17
|
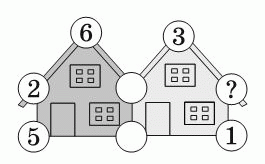
Сумма чисел в кружочках на краях каждого домика равна 20. Некоторые из этих чисел указаны на рисунке. Какое число должно быть в кружочке, отмеченном знаком вопроса?
A) 3 Б) 4 В) 7 Г) 9 Д) 14
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 39.5
Сумма трёх указанных чисел на домике слева равна 5 + 2 + 6 = 13. Ещё два числа – такие же, как у второго домика. Поэтому, чтобы суммы всех чисел у домиков были равными, необходимо, чтобы и у второго домика сумма трёх чисел 3, ? и 1 равнялась 13. Тогда искомое число ? = 13 – 3 – 1 = 9.
|
Задание 18
|
На следующих рисунках изображены газоны. Какой из них самый маленький?

|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 39.5 - 1.25 = 38.25
|
Разобьём газоны в вариантах ответа на равные треугольники.

Подсчитывая количества треугольников, получаем: газон А состоит из 7 треугольников, а остальные газоны – из 8 треугольников. Таким образом, самый маленький газон – газон А.
По-другому правильный ответ можно получить так. Добавим к данным газонам несколько треугольников так, как показано ниже.

Видим, что после этого все газоны становятся одинаковыми. Но в варианте А добавлено 3 треугольника, а в остальных вариантах – 2 треугольника. Следовательно, самым маленьким является газон А.
Задание 19
|
Каждый год Марии на день рождения дарили плюшевых мишек. На свой первый день рождения ей подарили 1 мишку, на второй – 2 мишки. На каждый следующий день рождения она получала на одного мишку больше, чем на предыдущий день рождения. Сколько всего плюшевых мишек подарили Марии за первые 6 лет?
A) 19 Б) 20 В) 21 Г) 22 Д) 23
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Согласно условию, за 6 лет Марии подарили 1 + 2 + 3 + 4 + 5 + 6 = 21 медвежонка.
|
Задание 20
|
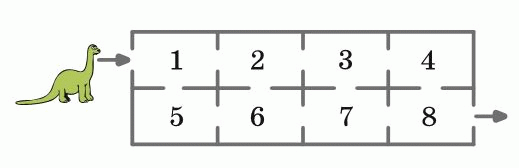
Дино идет сквозь здание от входа к выходу. Через каждую комнату он может пройти не более чем один раз. Проходя через комнаты, Дино складывает номера комнат. Какая наибольшая сумма может получиться у Дино, когда он выйдет из здания?
A) 27 Б) 29 В) 32 Г) 34 Д) 36
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Сумма всех номеров комнат равна 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. Но Дино не может пройти через все комнаты с соблюдением условия задачи. Из комнаты 1 он может пройти либо в комнату 2, либо 5. Но если он пройдёт из 1 в 2, то тогда в 5 можно будет попасть только из 6 и путь нельзя будет продолжить без повторения комнат. Следовательно, в этом случае сумма номеров пройденных комнат будет не больше 36 – 5 = 31.
Если начало пути будет 1 → 5 → 6, то продолжением может быть либо 6 → 2, либо 6 → 7.
В случае 1 → 5 → 6 → 2 продолжением может быть путь 2 → 3 → 4 → 8 → выход или 2 → 3 → 7 → 8 → выход. Но в первом случае будет пропущена комната 7, а во втором – комната 4. Тогда сумма номеров пройденных комнат будет не больше, соответственно, 36 – 7 = 29 и 36 – 4 = 32.
В случае 1 → 5 → 6 → 7 нельзя пройти через комнату 2. Действительно, в 2 можно будет попасть только из 3, после чего нельзя будет пройти к выходу. А все остальные комнаты пройти можно. Получаем
путь 1 → 5 → 6 → 7 → 3 → 4 → 8, который является самым длинным. Его длина равна 36 – 2 = 34.
|
Задание 21
|
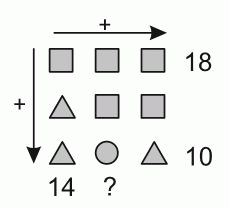
На рисунке фигуры обозначают числа (одинаковые фигуры – одинаковые числа, разные фигуры – разные числа). Суммы чисел в двух строчках и в одном столбце указаны. Чему равна сумма чисел в среднем столбце?
A) 10 Б) 12 В) 14 Г) 16 Д) 18
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Согласно условию, сумма трёх «квадратов» равна 18 (см. верхнюю строчку таблицы). Тогда один «квадрат» равен 18 : 3 = 6. Рассмотрим левый столбец. Сумма «квадрата», равного 6, и двух «треугольников» равна 14. Поэтому сумма двух «треугольников» равна 14 – 6 = 8. Тогда один «треугольник» равен 8 : 2 = 4. В нижней
строке сумма двух «треугольников», равных 4, и «кружочка» равна 10. Тогда «кружочек» равен 10 – 4 – 4 = 2. В результате, сумма чисел в среднем столбце равна 6 + 6 + 2 = 14.
|
Задание 22
|
На конкурсе красоты участвуют три зебры. Побеждает та, у которой больше всего полос. У Руны 15 полос, а у Зары на 3 полосы больше. У Руны на 5 полос меньше, чем у Бибы. Сколько полос у победительницы?
A) 16 Б) 18 В) 20 Г) 22 Д) 24
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 38.25 - 1.25 = 37
|
По условию, у Руны 15. Тогда у Зары 15 + 3 = 18 полос. А у Бибы столько полос, что если уменьшить их на 5, то получится, столько же, как у Руны. Поэтому у Бибы 15 + 5 = 20 полос. Видим, что победила Биба и у неё 20 полос.
Задание 23
|
Автомобиль Кенги может поворачивать только налево, но не может поворачивать направо. Какой из следующих маршрутов может быть маршрутом Кенги?

|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 37 - 1.25 = 35.75
|
Если в варианте А начать путь в точке, отмеченной белым кружочком, то все повороты будут поворотами налево. В остальных вариантах ответа синими и жёлтыми кружочками указаны повороты, которые не могут быть оба поворотами налево. Таким
образом, правильным является ответ А.

Задание 24
|

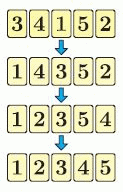
В ряд расположено пять карт так, как показано на рисунке. За один ход можно поменять местами любые две карты. За какое наименьшее число ходов можно расположить карты так, чтобы числа на них шли в порядке возрастания?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 35.75 - 1.25 = 34.5
|
Заметим, что ни одна из карт не находится на нужном месте. За один ход не более чем две карты можно расположить на нужные места. Поэтому все 5 карт за 2 хода расположить на нужные места нельзя. А за 3 хода это сделать можно, например, так, как показано на рисунке.