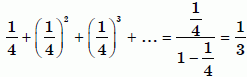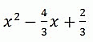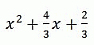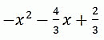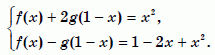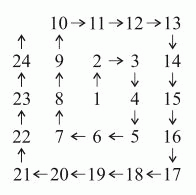Задание 1
|
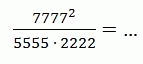
A) 1 Б) 7/10 В) 49/10 Г) 77/110 Д) 49
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Имеем:
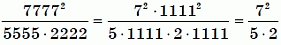 = 49/10
= 49/10
|
Задание 2
|
Юля бросила пять кубиков и получила 19 очков. Какое максимальное количество шестёрок она могла выбросить?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Юля не могла выбросить 3 шестёрки. Действительно, всего выброшено 5 кубиков. Если бы выпало 3 шестёрки, то на ещё два кубика пришлось бы 19 – 3 · 6 = 1 очко, что невозможно. Тем более Юля не могла выбросить более трёх шестёрок. Тогда бы сумма очков была бы заведомо больше 19. Две шестёрки могли быть, например, если выпали 6, 6, 5, 1, 1. Поэтому правильным является ответ 2.
|
Задание 3
|
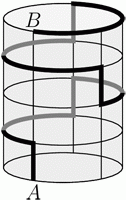
Цилиндрическая банка имеет высоту 15 см, а периметр ее круглого основания равен 30 см. Муравей ползёт по поверхности банки из точки А на нижнем основании в точку В на верхнем основании, как показано на рисунке. Все участки пути либо вертикальные, либо горизонтальные по дугам окружности. Какую длину имеет путь муравья?
A) 45 см Б) 55 см В) 60 см Г) 65 см Д) 75 см
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Вертикальные участки пути в совокупности составляют высоту банки и, значит, в сумме равны 15 см. Горизонтальные участки пути, если их спроецировать на нижнее основание банки, составят в точности 2 полные окружности основания. Поэтому путь муравья равен
15 + 2 · 30 = 75 см.
|
Задание 4
|

У Эммы есть четыре фломастера разного цвета. Она хочет раскрасить трёхполосный прямоугольный флаг так, чтобы каждая полоса была одного цвета, а любые две соседние полосы ─ разного цвета. Сколькими способами она может это сделать?
A) 24 Б) 27 В) 32 Г) 36 Д) 64
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Верхняя полоса может быть любого из 4-х цветов. Каждая полоса, расположенная ниже, может быть любого из 3 цветов (всех, кроме цвета полоски выше). Следовательно, флаг можно раскрасить
4 · 3 · 3 = 36 способами.
|
Задание 5
|
Натуральное число n будем называть 2-простым, если оно имеет ровно три различных натуральных делителя, а именно 1, 2 и само n. Сколько существует различных 2-простых чисел?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Легко видеть, что разложение 2-простого числа на простые множители должно иметь вид 2p. Если p ≠ 2, то такое число имеет делители 1, 2, p и 2p. Их четыре, а у 2-простого числа должно быть три делителя. Следовательно, p = 2 и, значит, существует только одно 2-простое число – число 4.
|
Задание 6
|
Сколько различных пар (x; y), где x, y – натуральные числа, удовлетворяют уравнению
x + 2y = 210
A) 29 - 1
Б) 29
В) 29 + 1
Г) 29 + 2
Д) 0
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Только если y принимает любое из значений от 1 до 29 – 1, то
2y < 210,
и тогда существует единственное натуральное значение
x = 210 – 2y, удовлетворяющее условию задачи.
Поэтому существует 29 – 1 пар, удовлетворяющих условию задачи.
|
Задание 7
|
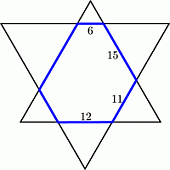
Два равносторонних треугольника в пересечении образуют шестиугольник, противоположные стороны которого параллельны. Длины четырёх сторон этого шестиугольника указаны на рисунке. Чему равен периметр этого шестиугольника?
A) 64 Б) 66 В) 68 Г) 70 Д) 72
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Поскольку соответствующие стороны двух данных треугольников параллельны,
то все «лучи» звезды, полученной в результате их объединения, являются равносторонними треугольниками. Тогда длина стороны AB треугольника ABC на рисунке равна
6 + 15 + 11 = 32.
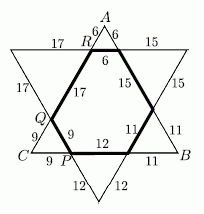
Но тогда и длина стороны BC этого треугольника также равна 32. Поэтому
CQ = PC = 32 – (12 + 11) = 9, и тогда
QR = 32 – (9 + 6) = 17.
В результате, искомый периметр равен
6 + 15 + 11 + 12 + 9 + 17 = 70.
|
Задание 8
|

Квадрат площадью 84 разбит на четыре квадрата. Верхний левый квадрат окрашен в чёрный цвет. Нижний правый квадрат также разбит на четыре квадрата, левый верхний из которых снова окрашен в чёрный цвет, и так далее, до бесконечности. Чему равна площадь чёрной части исходного квадрата?
A) 24 Б) 28 В) 31 Г) 35 Д) 42
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Первый чёрный квадрат по площади составляет 1/4 часть от всего данного квадрата. Следующий чёрный квадрат – 1/4 от предыдущего чёрного и т.д. до бесконечности. Получаем бесконечно убывающую геометрическую прогрессию, у которой первый член и знаменатель равны 1/4. По формуле суммы бесконечно убывающей прогрессии
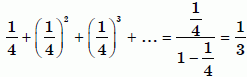
Поэтому площадь чёрной части данного квадрата равна
1/3 ⋅ 84 = 28.
|
Задание 9
|

Миша вписывает каждое из чисел от 1 до 9 в девять клеток полоски (в каждую – ровно одно число). Он хочет, чтобы суммы чисел в любых трёх последовательных клетках были кратны 3. Числа 7 и 9 Миша уже вписал так, как показано на рисунке. Сколькими способами он может заполнить оставшиеся клетки?
A) 9 Б) 12 В) 15 Г) 18 Д) 24
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Рассмотрим 4 подряд идущих числа. Первые 3 из них и последние 3 из них должны иметь суммы, кратные 3. При этом два слагаемых у этих сумм общие. Поэтому первое и четвёртое числа должны иметь одинаковые остатки при делении на 3. Следовательно, остатки чисел в строке должны повторяться с периодом 3, т.е. последовательность остатков чисел данной полоски имеет вид ABCABCABC, где A = 0, B = 1, C = 2. (Согласно условию, второе число, т.е. число 7, имеет остаток B, откуда B = 1. Четвёртое число, т.е. число 9, имеет остаток A, откуда A = 0. В результате остаток C = 2.) Одно из чисел с остатком 0 и одно из чисел с остатком 1 уже вписаны. В каждом случае остаётся по два числа с данными остатками. В соответствии со схемой чередования остатков в две оставшиеся клетки их можно вписать 2 способами. Далее, имеется
3! = 3 · 2 · 1 = 6 способов, как можно вписать 3 числа с остатком 1 в 3 соответствующие клетки.
Таким образом, Миша может заполнить оставшиеся клетки полоски
2 · 2 · 6 = 24 способами.
|
Задание 10
|
Какой цифрой заканчивается число, равное произведению
(55 + 1)(510 + 1)(515 + 1)?
A) 1 Б) 2 В) 4 Г) 5 Д) 6
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Число вида 5n при любом натуральном n заканчивается цифрой 5.
Тогда число вида 5n + 1 заканчивается цифрой 6. Поэтому данное в условии произведение заканчивается такой же цифрой, как произведение
6 · 6 · 6, т.е. цифрой 6.
|
Задание 11
|
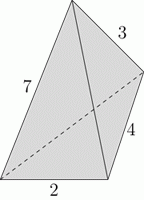
Треугольная пирамида имеет рёбра целочисленной длины. Длины четырёх из этих рёбер показаны на рисунке. Чему равна сумма длин двух других рёбер?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Рассмотрим треугольник BCD на рисунке.
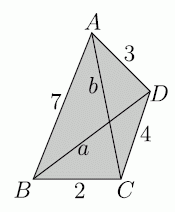
Согласно неравенству треугольника, (длина ребра BD):
a < 2 + 4 = 6.
С другой стороны, рассматривая треугольник АВD, получаем:
a + 3 > 7, откуда a > 4.
Из двойного неравенства 4 < a < 6 следует, что целое значение a = 5. Далее, в треугольнике АВC имеем:
b + 2 > 7, откуда b > 5.
С другой стороны, в треугольнике АCD:
b < 3 + 4 = 7.
Единственное целое значение b, удовлетворяющее обоим полученным неравенствам, – это b = 6. Таким образом, искомая сумма длин
a + b = 5 + 6 = 11.
|
Задание 12
|
Пусть n – натуральное число. Выражение n! означает произведение всех натуральных чисел от 1 до n включительно.
Например, 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 24.
Чему равна сумма цифр числа N, если N! = 6! ∙ 7! ?
A) 1 Б) 2 В) 4 Г) 8 Д) 9
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Имеем: N! = 6! · 7! = 7! · 1 · 2 · 3 · 4 · 5 · 6 = 7! · (2 · 4) · (3 · 3) · (5 · 2) = 7! · 8 · 9 · 10 = 10!.
Поэтому число N = 10, сумма его цифр равна 1 + 0 = 1.
|
Задание 13
|
Пусть графики всех функций вида
y = x3 + 3x2 + ax + 2a + 4
проходят через одну точку, независимо от значения а. Чему равна сумма координат этой точки?
A) 2 Б) 4 В) 7 Г) 8 Д) другой ответ
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
При a = 0 получаем:
y = x3 + 3x2 + 4.
При a = 1 получаем:
y = x3 + 3x2 + x + 6.
Вычтем первое уравнение из второго, получим
0 = x + 2, откуда x = –2.
Подставив это значение, например, в первое уравнение, получим
y = (–2)3 + 3(–2)2 + 4 = 8.
Поэтому искомая точка – это точка (–2; 8), сумма её координат равна –2 + 8 = 6. Следовательно, правильным является ответ Д.
Нетрудно показать, что найденная точка действительно принадлежит графикам функций вида
y = x3 + 3x2 + аx + 2а + 4
при всех действительных значениях а. Это следует из равенства
при всех действительных значениях а. Это следует из равенства
y = x3 + 3x2 + аx + 2а + 4 = (x + 2) · (x2 + x + a – 2) + 8.
Это равенство можно получить как результат деления данного кубического многочлена на x + 2 с остатком.
|
Задание 14
|
Сумма пяти чисел a1, a2, a3, a4, a5 равна S.
Для любого k, 1 ≤ k ≤ 5, верно равенство ak = S + k. Чему равно значение S?
A) 15/4
Б) -15/4
В) -15
Г) 15
Д) другой ответ
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Сложив пять данных равенств, получим:
a1 + a2 + a3 + a4 + a5 = 5S + 1 + 2 + 3 + 4 + 5,
или S = 5S + 15, откуда S =-15/4
|
Задание 15
|
Сколько различных пар (m; n), где m, n – целые числа, удовлетворяют неравенству
|2m - 2023| + |2n - m| ≤ 1 ?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Поскольку 2m – 2023 – нечётное число, наименьшее значение |2m – 2023| равно 1. Тогда неравенство
|2m – 2023| + |2n – m| ≤ 1
может быть выполнено только при условии, что
|2n – m| =0 и |2m – 2023| = 1.
Из уравнения
|2m – 2023| = 1 получаем
2m – 2223 = ±1, откуда 2m = 2022 или 2024, т.е. m = 1011 или m =1012.
Подставим эти значения в уравнение
|2n – m|=0.
В первом случае получим
|2n – 1011| = 0 – нет целых решений, так как 2n – 1011 – нечётное число.
Во втором случае получим
|2n – 1012| = 0, или 2n – 1012 = 0, откуда n = 506.
Таким образом, существует только 1 пара (m; n) = (1012; 506), удовлетворяющая условию задачи.
|
Задание 16
|
В кинотеатре в первом ряду сидят 23 животных. Каждое из них либо бобёр, либо кенгуру. У каждого животного в этом ряду хотя бы один из соседей – кенгуру. Какое наибольшее количество бобров может быть в этом ряду?
A) 7 Б) 8 В) 10 Г) 11 Д) 12
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Заметим, что в любой четвёрке последовательно сидящих животных не более двух бобров. Действительно, если конфигурация расположения животных имеет вид ББББ, БББК или БКББ, то по крайней мере у второго слева животного условие задачи не выполняется. (С точностью до симметрии, эти 3 конфигурации – все, в которых более двух бобров.) Итак, в каждой четвёрке последовательно сидящих животных не более двух бобров и, значит, не менее двух кенгуру. Заметим также, что два подряд бобра не могут сидеть с краю на двух первых или на двух последних местах (у первого и последнего животного не будет соседнего кенгуру). Поэтому максимальное число бобров даёт рассадка: БККБ БККБ БККБ БККБ БККБ
БКК. В ней 11 бобров.
|
Задание 17
|
Число 556 можно представить в виде nn. Чему равно n?
A) 530 Б) 56 В) 55 Г) 30 Д) 11
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Имеем:
556 = 55⋅55 = (55)55
(в последнем преобразовании использована формула akm = (ak)m).
Поэтому n = 55.
|
Задание 18
|
Леон нарисовал на поверхности прямоугольного параллелепипеда замкнутый путь. В каком из следующих ответов может быть изображена развёртка поверхности данного параллелепипеда?

|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
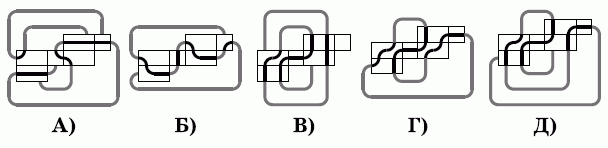
Проведённые линии, расположенные вне развёрток, показывают, с какими гранями будут соединены концы линий на гранях развёрток, если их свернуть обратно в поверхность параллелепипеда. Видим, что только в случае Г получается непрерывная линия. Это значит, что при сворачивании этой развёртки на поверхности параллелепипеда будет непрерывная линия. Таким образом, правильным является ответ Г.
|
Задание 19
|
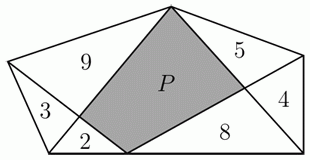
Пятиугольник разбит на несколько частей, как показано на рисунке. Числа внутри треугольников указывают их площади. Чему равна площадь серого четырехугольника?
A) 15 Б) 15,5 В) 16 Г) 17 Д) 18
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Проведём диагональ заштрихованного четырёхугольника, как показано на рисунке.
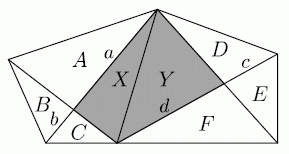
Треугольники A и B имеют одинаковые
высоты, опущенные на основания a и b соответственно. При этом площадь треугольника A (обозначим её тоже буквой A, аналогично будем обозначать площади других фигур) A = 3B. Тогда аналогично относятся длины оснований треугольников A и B, т.е. a = 3b. Но a и b являются также основаниями треугольников X и C с общей высотой, проведённой к ним. Поэтому
X = 3C = 3 · 2 = 6.
Аналогично, Y : D = d : c = Y : D = 8 : 4 = 2.
Поэтому Y = 2D = 2 · 5 = 10.
В результате площадь серого четырёхугольника равна
X + Y = 6 + 10 = 16.
Немного быстрее можно получить ответ, если воспользоваться свойством площадей треугольников, на которые диагонали разбивают выпуклый четырёхугольник. Согласно этому свойству,
X · B = A · C (эту формулу можно доказать, рассуждая, как в приведённом выше решении; существуют и другие способы доказательства). Тогда
X = (A · C) : B.
Аналогично,
Y = (D · F) : E.
Поэтому
X + Y = (9 · 2) : 3 + (5 · 8) : 4 = 6 + 10 = 16.
|
Задание 20
|
Сколько делителей числа 220 ∙ 323 не являются делителями числа 210 ∙ 320 ?
A) 13 Б) 30 В) 273 Г) 460 Д) другой ответ
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Заметим, что всякий делитель числа 210 · 320 является также делителем числа 220 · 323. Делители каждого из этих чисел имеют вид 2n · 3m. Но для первого числа их количество, т.е. число подходящих пар (n; m), равно
(20 + 1) · (23 + 1) = 504,
а для второго –
(10 + 1) · (20 + 1) = 231.
Поэтому число делителей числа 220 · 323, которые не являются делителями числа 210 · 320 равно
504 – 231 = 273.
|
Задание 21
|
Две функции f(x) и g(x), заданные на множестве действительных чисел, удовлетворяют уравнениям
f(x) + 2g(1 - x) = x2 и
f(1 - x) - g(x) = x2
при всех значениях x. Найдите формулу, задающую функцию f(x).
A) 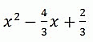
Б) 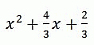
В) 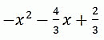
Г) x2 - 4x + 5
Д) такой функции не существует
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Подставив во второе уравнение (1 – x) вместо x, получим
f(x) – g(1 – x) = 1 – 2x + x2.
Вместе с первым уравнением имеем систему:
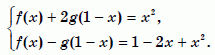
Умножим второе уравнение системы на 2 и сложим результат с первым уравнением. Получим
3f(x) = 3x2 – 4x + 2, откуда
f x = x2 – 4/3x + 2/3.
|
Задание 22
|
В соревнованиях по боулдерингу 13 альпинистов соревнуются в трёх категориях. Оценка каждого участника является произведением его рейтингов в трёх категориях. Например, если спортсмен занимает 4-е, 3-е и 6-е места, его оценка будет равна
4 • 3 • 6 = 72.
Чем выше оценка, тем ниже общий рейтинг на соревнованиях. Анна заняла 1-е место в двух категориях. Какой самый низкий общий рейтинг у неё может быть?
A) 2-й Б) 3-й В) 4-й Г) 5-й Д) 6-й
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Если Анна заняла 1-е место в двух категориях, то её наибольшая оценка равна
1 · 1 · 13 = 13.
Далее, по крайней мере два участника могли получить меньшие оценки, например,
2 · 2 · 2 = 8 и
3 · 3 · 1 = 9.
Покажем, что таких участников не более двух. Предположим противное: их по крайней мере 3. Тогда их места в первой категории не меньше 2, 3 и 4; во второй – также не меньше 2, 3 и 4; в третьей – не меньше 1, 2, 3. Тогда произведение оценок этих трёх участников не меньше
23 · 33 · 42 = 3456.
Но если бы у всех трёх этих участников оценки были не более 13, то произведение этих оценок было бы не более
133 = 2197.
Но 3456 > 2197. Поэтому Анну могли опередить только два участника и, значит, её самый низкий рейтинг – 3-й.
|
Задание 23
|
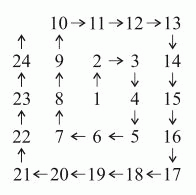
Спираль из последовательных натуральных чисел строится, начиная с 1, как показано выше. Если построение спирали будет продолжено, то как в ней будут располагаться числа 625, 626 и 627?
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Будем считать, что числа вписываются по спирали в клетки большого клетчатого листа. Рассмотрим квадраты, состоящие из клеток, у которых в центре записано число 1. Первый из них – это квадрат со стороной 1, состоящий из одной клетки. Следующий – квадрат со стороной 3, состоящий из 32 = 9 клеток, в которые вписаны числа от 1 до 9, последнее число 9 – в левом верхнем углу.
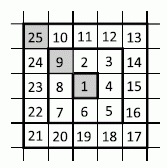
Далее идёт квадрат со стороной 5, состоящий из 52 = 25 клеток, последнее из них число 25 также вписано в левом верхнем углу. Согласно тому, как продолжается данная спираль, все следующие квадраты, в центре которых находится 1, будут иметь нечётные размеры, причём наибольшее в квадрате со стороной 2n – 1 число (2n – 1)2
будет вписано в левом верхнем углу данного квадрата. Поскольку число 625 = 252, то оно будет вписано в левом верхнем углу квадрата со стороной 25. Следующее число 626, по ходу данной спирали будет записано выше числа 625, а число 627 – правее числа 626. Поэтому правильным является ответ Б.
|
Задание 24
|
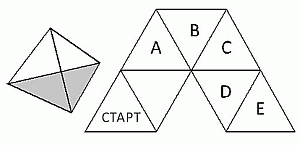
У правильного тетраэдра одна грань серая. Тетраэдр серой гранью поставили на плоскость в треугольнике с надписью START. Затем тетраэдр начали перекатывать через рёбра по пути, указанному на рисунке. На какой из треугольников снова впервые после старта тетраэдр встанет серой гранью?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Пусть P, Q, R и S – вершины данного тетраэдра, где P, Q, R – вершины его серой грани. На следующем рисунке указаны вершины нижних граней после перекатываний.
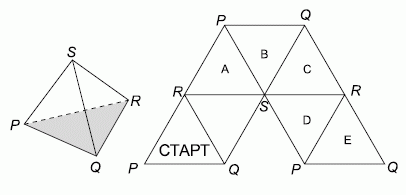
Видим, что впервые после старта основание тетраэдра совпадёт с основанием на старте в треугольнике Е.
|
Задание 25
|

Часть многочлена пятой степени на рисунке не видна из-за чернильного пятна. Известно, что многочлен имеет (с учётом кратности) пять целых корней. На какую наибольшую степень (x – 1) делится данный многочлен?
A) (x – 1)1
Б) (x – 1)2
В) (x – 1)3
Г) (x – 1)4
Д) (x – 1)5
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Согласно формулам Виета для многочлена 5-й степени, произведение корней данного многочлена равно свободному члену со знаком минус, т.е. числу 7. (Формулы Виета для такого многочлена получатся, если раскрыть скобки в выражении
(x – a1)(x – a2)(x – a3)(x – a4)(x – a5), где a1, a2, …, a5 – корни данного многочлена, и посчитать, как через эти корни выражается свободный член и другие коэффициенты при степенях х данного многочлена.)
Поэтому, если все корни данного многочлена – целые числа, то ими могут быть только какие-то из чисел ±1 и ±7, причём ровно один из корней равен 7 или –7.
Далее, по ещё одной формуле Виета, сумма корней (снова со знаком минус) равна коэффициенту при x4, т.е., по условию, равна 11. Но из названных возможных значений корней существует только один способ получить сумму 11 – это
11 = 7 + 1 + 1 + 1 +1.
Следовательно, корень 1 имеет кратность 4. Поэтому наибольшая степень (x – 1), на которую
делится данный многочлен, – это (x – 1)4.
|
Задание 26
|
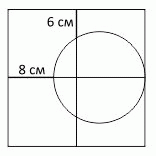
Квадрат на рисунке разбит на четыре меньших квадрата. Окружность касается правой стороны квадрата в её середине. Какую длину имеет сторона исходного квадрата? (Обратите внимание, что схема нарисована не в масштабе.)
A) 18 см Б) 20 см В) 24 см Г) 28 см Д) 30 см
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Проведём хорды AB и BC и рассмотрим треугольник ABC (см. рис.).
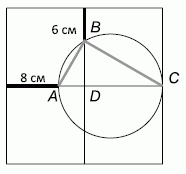
Так как вписанный угол ABC опирается на диаметр окружности, этот угол является прямым. Пусть 2а (см) – сторона исходного квадрата. Тогда
AD = a – 8, BD = a – 6, DC = a.
В прямоугольном треугольнике ABC по свойству высоты, проведённой к гипотенузе, имеем:
BD2 = AD · DC, т.е.
(a – 6)2 = (a – 8) · a, откуда a = 9.
Поэтому сторона исходного квадрата 2a = 18 (см).
|
Задание 27
|
Чему равен наибольший общий делитель всех чисел вида
n3 (n + 1)3 (n + 2)3 (n + 3)3 (n + 4)3
при всех натуральных n?
A) 29 33
Б) 23 33 53
В) 26 33 53
Г) 28 32 53
Д) 29 33 53
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
При n = 1 получаем число
13 · 23 · 33 · 43 · 53 = 293353.
Поэтому НОД всех чисел указанного вида является делителем числа 293353, в частности, не больше этого числа.
Покажем, что искомый НОД равен указанному числу.
Действительно, произведение
n(n + 1)(n + 2)(n + 3)(n + 4)
есть произведение пяти последовательных натуральных чисел. Среди них обязательно есть число, кратное 3 (достаточно взять любые три последовательных числа), есть число, кратное 5. Кроме того, есть число, кратное 4 (достаточно четырёх последовательных чисел), и ещё хотя бы одно чётное число. Поэтому произведение данных пяти натуральных чисел делится на
23 · 3 · 5.
Тогда куб данного произведения, т.е.
n3(n + 1)3 (n + 2)3 (n + 3)3 (n + 4)3
делится на
(23 · 3 · 5)3 = 293353.
|
Задание 28
|
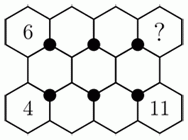
Числа от 1 до 11 нужно вписать в ячейки на рисунке так, чтобы суммы трёх чисел вокруг каждой из шести чёрных отмеченных точек были одинаковы. Три числа уже вписаны, как показано на рисунке. Какое число должно быть вписано в ячейку со знаком вопроса?
A) 1 Б) 3 В) 5 Г) 7 Д) 9
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Обозначим числа в пустых ячейках так, как показано на рис.1.
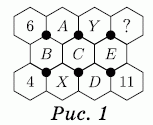
Рассматривая две левые чёрные точки, получаем
6 + A + B = 4 + B + X, откуда
X = A + 2.
Тогда, рассматривая две средние чёрные точки, получаем
A + Y + C = (A + 2) + C + D, откуда
Y = D + 2.
Наконец, рассмотрим две крайние правые чёрные точки. С учётом полученного выше результата, имеем:
(D + 2) + ? + E = D + E + 11, откуда
? = 9.
Хотя этого не требуется, можно найти значения во всех ячейках. Они вычисляются однозначно и указаны на рис.2.
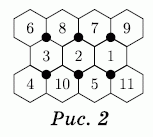
|
Задание 29
|
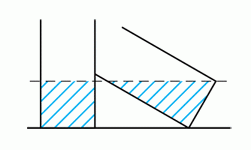
Два одинаковых цилиндрических резервуара для воды содержат одинаковое количество воды. Один цилиндр стоит вертикально, а другой прислонен к нему, и уровни воды в них одинаковые (см. рис.). Дно каждого из цилиндров представляет собой круг площадью 3π м2. Сколько воды находится в каждом из резервуаров?
A) 3√3π м3
Б) 6π м3
В) 9π м3
Г) 3/4 π м3
Д) недостаточно данных, чтобы определить однозначно
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Из формулы площади круга сразу получаем, что радиусы оснований данных цилиндров равны r = √3.
В первом (стоящем прямо) цилиндре осевым сечением тела, которое занимает вода, является прямоугольник 2r × h, а во втором (наклоненном) цилиндре – прямоугольный треугольник с катетами 2r и l (см. рис.).
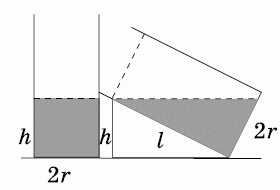
Из соображений симметрии ясно, что если поставить наклонный цилиндр прямо и залить в него воды до уровня l, то воды станет в 2 раза больше. Поэтому l = 2h. Следовательно, прямоугольный треугольник (на рисунке) с катетом h и гипотенузой l имеет углы, равные 30° и 60°. Тогда из прямоугольного треугольника с катетами l = 2h и 2r получаем
h : r = 2h : 2r = tg 60° = √3.
Поэтому h = √3r = √3 · √3 = 3.
Следовательно, в каждом цилиндре содержится
3 · 3π = 9π м3 воды.
|
Задание 30
|
Произведение шести последовательных чисел равно 12-значному числу вида
abb cdd cdd abb,
где цифры a, b, c и d сами являются четырьмя последовательными числами в некотором порядке.
Каково значение цифры d?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
Среди шести последовательных множителей имеются (три) чётных числа и по крайней мере одно число, кратное 5. Поэтому произведение данных шести чисел делится на 2 · 5 = 10 и, значит, b = 0. Тогда, поскольку цифры a, b, c и d – последовательные числа, цифры a, c и d – это цифры 1, 2 и 3 в некотором порядке. В частности,
а + с + d = 6.
Далее, заметим, что среди шести последовательных множителей два множителя кратны 3. Поэтому произведение данных шести чисел, а значит, и сумма его цифр, кратны 9. Кроме того, сумма цифр – чётная, так как данное 12-значное число состоит из двух пар одинаковых троек цифр. Поэтому половина суммы цифр также должна быть кратна 9. Учитывая, что b = 0, а остальные цифры не более 3, можно сделать вывод, что половина суммы цифр
а + с + 2d = 9.
Из этого уравнения и уравнения
а + с + d = 6
следует, что d = 3.
Хотя правильный ответ уже найден, продолжив это исследование, можно найти а = 2 и с = 1. Кроме того, можно найти сами множители:
74 · 75 · 76 · 77 · 78 · 79 = 200 133 133 200.
|
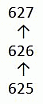
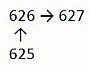
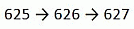
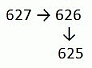
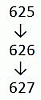














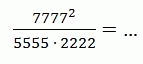
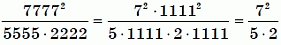 = 49/10
= 49/10