Задание 1
|
На каком облаке все числа чётные?
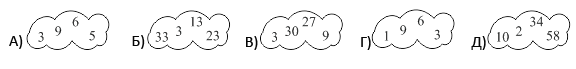
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Задание 2
|
Сколько часов составляют десять четвёртых часа?
A) 40 Б) 5,5 В) 4 Г) 3 Д) 2,5
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Задание 3
|
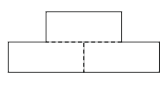
Фигура на рисунке состоит из трёх равных прямоугольников. Каждый прямоугольник имеет периметр 14 см. Чему равен периметр фигуры?
A) 28 см
Б) 32 см
В) 35 см
Г) 42 см
Д) другой ответ
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Задание 4
|
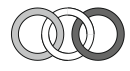
Три кольца соединены так, как показано на рисунке. В каком из следующих ответов эти три кольца соединены так же?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 31.5 + 3 = 34.5
|
Задание 5
|
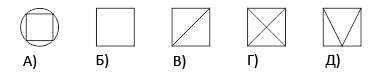
Какой из следующих рисунков нельзя нарисовать, не отрывая карандаш от бумаги и не проводя ни одной линии дважды?
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 34.5 + 3 = 37.5
|
Задание 6
|

Встретились 5 друзей. Каждый из них дал каждому другу по 1 конфете. Все полученные конфеты друзья съели. В результате общее число конфет у друзей уменьшилось наполовину. Сколько всего конфет было у друзей до встречи?
A) 20 Б) 34 В) 30 Г) 40 Д) 60
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.5 + 3 = 40.5
|
Задание 7
|
В гонке Лотар финишировал раньше, чем Манфред, Виктор финишировал после Яна, Манфред финишировал раньше, чем Ян, а Эдди финишировал раньше Виктора. Кто финишировал последним из этих пяти участников гонки?
A) Виктор Б) Манфред В) Лотар Г) Ян Д) Эдди
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Задание 8
|
Страницы брошюры пронумерованы числами, начиная с 1. Цифра 0 использована при записи этих чисел пять раз, а цифра 8 – ровно шесть раз. Каков номер последней страницы?
A) 48 Б) 58 В) 60 Г) 68 Д) 88
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 43.5 + 3 = 46.5
|
Задание 9
|
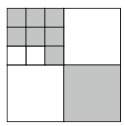
Квадрат (см. рис.) состоит из меньших квадратов. Какая часть этого квадрата окрашена в серый цвет?
A) 2/3 Б) 2/5 В) 4/7 Г) 4/9 Д) 5/12
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 46.5 + 3 = 49.5
|
Задание 10
|
Андрей разделил имеющееся у него количество яблок на шесть равных куч. А Борис разделил такое же количество яблок на пять равных куч. Борис заметил, что в каждой его куче на два яблока больше, чем в каждой из куч Андрея. Сколько яблок было у Андрея?
A) 60 Б) 65 В) 70 Г) 75 Д) 80
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 49.5 + 3 = 52.5
|
Задание 11
|
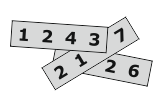
На каждой из трёх полосок бумаги написано четырёхзначное число (см. рис.). Сумма этих трёх чисел равна 10126. Три цифры у этих чисел скрыты. Какие это цифры?
A) 5, 6 и 7
Б) 4, 5 и 7
В) 4, 6 и 7
Г) 4, 5 и 6
Д) 3, 5 и 6
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 52.5 + 4 = 56.5
|
Задание 12
|
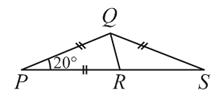
На рисунке PQ = PR = QS и ∠QPR=20°. Найдите ∠RQS.
A) 50° Б) 60° В) 65° Г) 70° Д) 75°
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 56.5 - 1 = 55.5
|
Задание 13
|
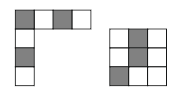
Какой из следующих квадратов нельзя составить из двух фигур на рисунке сверху?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 55.5 + 4 = 59.5
|
Задание 14
|
Александр, Борис, Владимир, Григорий и Дмитрий встретились на вечеринке и пожали руки тем, с кем они знакомы. Александр пожал руку один раз, Борис – два раза, Владимир – три раза, а Григорий – четыре раза. Сколько раз пожал руки Дмитрий?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 59.5 - 1 = 58.5
|
Задание 15
|
Джейн играет в баскетбол. В серии из 20 бросков она попала в корзину 55% раз. После ещё пяти бросков её общий процент попаданий стал равен 56%. Сколько из последних пяти бросков оказались успешными?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 58.5 - 1 = 57.5
|
Задание 16
|
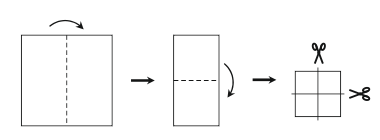
Катя сложила квадратный лист бумаги два раза, а затем разрезала его два раза так, как показано на рисунке. Сколько всего квадратных кусков бумаги она получит, если развернуть все полученные части?
A) 3 Б) 4 В) 5 Г) 6 Д) 8
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 57.5 + 4 = 61.5
|
Задание 17
|
У бабушки в деревне 24 питомца: собаки, коты, коровы и кенгуру. Она сообщила своей внучке Елене, что восьмая часть из них – собаки, три четверти – не коровы, и две трети – не коты. Сколько особей кенгуру у бабушки?
A) 4 Б) 5 В) 6 Г) 7 Д) 8
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 61.5 + 4 = 65.5
|
Задание 18
|
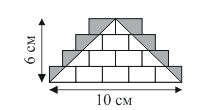
Фигура на рисунке состоит из одинаковых прямоугольников. Чему равна площадь серой части этой фигуры?
A) 10 см2
Б) 12 см2
В) 14 см2
Г) 15 см2
Д) 16 см2
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 65.5 - 1 = 64.5
|
Задание 19
|
У Юли есть две цилиндрические свечи разной высоты и диаметра. Первая свеча сгорает за 6 часов, а вторая – за 8 часов. Юля зажгла обе свечи одновременно, и через три часа обе свечи стали одинаковой высоты. Каково было соотношение их первоначальных высот?
A) 4 : 3
Б) 8 : 5
В) 5 : 4
Г) 3 : 5
Д) 7 : 3
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 64.5 + 4 = 68.5
|
Задание 20
|

Оля хочет построить замкнутый путь из спичек, располагая их в точности по сторонам клеток. Длина спички равна стороне клетки. Одну спичку она уже положила так, как показано на рисунке. Для некоторых клеток указаны количества спичек, которые должны лежать на сторонах этих клеток. Какое наименьшее количество спичек может быть на этом пути?
A) 12 Б) 14 В) 16 Г) 18 Д) 20
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 68.5 - 1 = 67.5
|
Задание 21
|
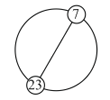
Натуральные числа от 1 до n включительно записаны по кругу по порядку через равные промежутки. Диаметрально противоположным числу 7 оказалось число 23. Чему равно n?
A) 30 Б) 32 В) 34 Г) 36 Д) 38
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 67.5 + 5 = 72.5
|
Задание 22
|
Коммерсант Лёня потратил все свои деньги на покупку 50 бутылок минералки по 1 рублю каждая. Он продал все бутылки по одной и той же более высокой цене. После продажи 40 бутылок у него оказалось на 10 рублей больше, чем было в начале. Сколько денег стало у Лёни после продажи всех бутылок?
A) 70 руб Б) 75 руб В) 80 руб Г) 90 руб Д) 100 руб
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 72.5 - 1.25 = 71.25
|
Задание 23
|

У Наташи есть одинаковые палочки синего, красного, жёлтого и зелёного цвета. Она хочет построить клетчатый квадрат на рисунке так, чтобы у каждой клетки все стороны были разного цвета. Какое наименьшее количество зелёных палочек ей понадобится?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 71.25 - 1.25 = 70
|
Задание 24
|
Муравей ползает по замкнутой линии на поверхности куба. На каком из следующих рисунков изображена развёртка поверхности такого куба?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 70 - 1.25 = 68.75
|
Задание 25
|
У Лизы было 60 конфет. В понедельник она съела одну десятую часть из них, во вторник – одну девятую из оставшихся, в среду – одну восьмую из оставшихся и так далее, пока не съела половину из оставшихся в предыдущий день конфет. Сколько конфет у нее осталось?
A) 1 Б) 2 В) 3 Г) 4 Д) 6
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 68.75 - 1.25 = 67.5
|
Задание 26
|
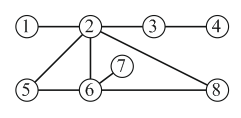
Петя окрасил каждый из восьми кружочков на диаграмме красным, жёлтым или синим цветом так, что никакие два кружочка, соединённые отрезком, не были окрашены в один цвет. Какие два кружочка обязательно окрашены в один цвет?
A) 5 и 8
Б) 1 и 6
В) 2 и 7
Г) 4 и 5
Д) 3 и 6
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 67.5 - 1.25 = 66.25
|
Задание 27
|
Когда Рита и Вера сравнили свои сбережения, они обнаружили, что они относятся как 5 : 3. Но когда Рита купила планшет за 160 руб., то их сбережения стали относиться как 3 : 5. Сколько денег было у Риты до покупки планшета?
A) 192 руб. Б) 200 руб. В) 250 руб. Г) 400 руб. Д) 420 руб.
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 66.25 - 1.25 = 65
|
Задание 28
|
Несколько команд, состоящих из трёх игроков, могут принять участие в шахматном турнире. Каждый игрок одной команды должен сыграть ровно одну партию с каждым игроком из всех других команд. По организационным причинам число всех партий не должно быть больше 250. Какое наибольшее число команд может принять участие в этом турнире?
A) 11 Б) 10 В) 9 Г) 8 Д) 7
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 65 - 1.25 = 63.75
|
Задание 29
|
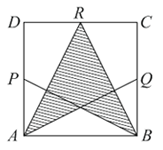
Точки P, R и Q являются серединами соответствующих сторон квадрата ABCD на рисунке справа. Какая часть площади этого квадрата заштрихована?
A) 3/4 Б) 5/8 В) 1/2 Г) 7/16 Д) 3/8
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 63.75 + 5 = 68.75
|
Задание 30
|
В 18 вагонах поезда едут 700 пассажиров. В любых пяти подряд идущих вагонах находится 199 пассажиров. Сколько пассажиров находится в двух средних вагонах?
A) 70 Б) 77 В) 378 Г) 96 Д) 103
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 68.75 + 5 = 73.75
|