Задание 1
|

Какая из следующих плиток дополняет узор на рисунке?
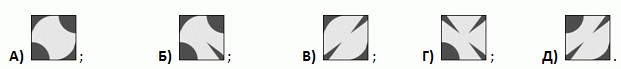
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Дорисуем в центральной клетке
недостающие фрагменты узора (см. рис.).

Сравнивая результат с вариантами ответа, видим, что правильным является ответ Д.
Задание 2
|
Тамара едет из Атауна в Бетаун. По дороге она проезжает мимо следующих указателей. Один из них неправильный. Который?

|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Из данных на указателях следует, что расстояние между Атауном в Бетауном равно:
А) 2 + 9 = 11,
Б) 3 + 8 = 11,
В) 5 + 6 = 11,
Г) 8 + 3 = 11,
Д) 9 + 4 = 13.
Видим, что результат в случае Д) отличается от остальных. Поэтому правильным является ответ Д.
Задание 3
|

Квадрат на рисунке состоит из белых и серых клеток. Как он будет выглядеть, если серые клетки поменять на белые, а белые – на серые?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Отметим крестиками все белые клетки квадрата на рисунке в условии задачи (см. рис.).

Сравнивая их расположение с расположением серых клеток в вариантах ответа, видим, что правильным является ответ Г.
Задание 4
|
Миша хочет испечь 24 блинчика для своих друзей на его день рождения. Чтобы испечь 6 блинчиков, нужны 2 яйца. Яйца продаются в коробках по 6 штук. Какое наименьшее число коробок яиц Мише нужно купить?
A) 1 Б) 2 В) 3 Г) 4 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 35.25 - 0.75 = 34.5
|
Из условия следует, что для того, чтобы испечь 3 блинчика, нужно 1 яйцо. Следовательно, чтобы испечь 24 блинчика, нужно
24 : 3 = 8 яиц.
В одной коробке находится 6 яиц. Видим, что одной коробки недостаточно. А двух коробок достаточно, поскольку в них находится
6 · 2 = 12 > 8 яиц.
Поэтому правильным является ответ 2.
Задание 5
|
У Кати есть несколько цепочек, состоящих из 5 или 7 бусинок. Катя хочет связать их в круг, чтобы получились бусы. Сколько бусинок не может быть в полученных бусах?
A) 10 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 34.5 - 0.75 = 33.75
|
Бусы в вариантах ответа А), Б), Г) и Д) получить можно. Это видно из следующих равенств.
А) 10 = 5 + 5;
Б) 12 = 5 + 7;
Г) 14 = 7 + 7;
Д) 15 = 5 + 5 + 5.
Поэтому правильным может быть только ответ В.
Покажем непосредственно, что это так. Бусы, состоящие из 13 бусинок, нельзя получить, использовав две или более цепочек с 7 бусинками, иначе бусы состояли бы не менее чем из 14 бусинок. Если использована только одна такая цепочка, то остальные
13 – 7 = 6 бусинок нужно получить с помощью цепочек с 5 бусинками. Ясно, что это невозможно, так как 6 не делится на 5. Если не использована ни одна цепочка с 7 бусинками, то все 13 бусинок нужно получить с помощью цепочек с 5 бусинками. Это также невозможно, поскольку 13 не делится на 5.
Задание 6
|

Федя отразил симметрично букву F относительно вертикальной прямой и относительно горизонтальной прямой на рисунке. Что у него получилось?

|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 33.75 - 0.75 = 33
|

На рис. 1 и 2 показаны отражения данной фигуры относительно вертикальной и относительно горизонтальной прямых соответственно. Объединив эти два отражения, получим результат на рис. 3. Исключив на рис. 3 исходную фигуру и сравнивая результат с вариантами ответа, видим, что верным является ответ Д.
Задание 7
|
У Маши было 10 листов бумаги. Она разрезала некоторые их них на 5 частей каждый. В результате всего у неё получилось 22 листа. Сколько листов Маша разрезала?
A) 3 Б) 2 В) 6 Г) 7 Д) 8
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 33 - 0.75 = 32.25
|
Каждый раз, когда Маша разрезает лист на 5 частей, число листов увеличивается на 4 (разрезанный лист исчезает, а вместо него появляются 5 новых). Согласно условию, в результате всех разрезаний число листов увеличилось на 22 – 10 = 12 штук. Поэтому всего было разрезано 12 : 4 = 3 листа.
Задание 8
|
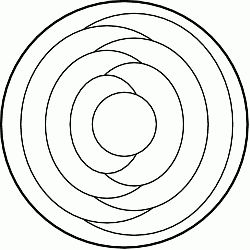
Синди раскрашивает каждую часть круга на рисунке в красный, синий или жёлтый цвет. Части, имеющие общую границу, должны быть окрашены в разные цвета. Внешнюю часть она окрасила в синий цвет. Сколько всего частей Синди окрасит в синий цвет?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Начнём с синей внешней части и продолжим окраску, продвигаясь к центру. В результате может получиться только два способа полной окраски, удовлетворяющей условию задачи. Один из них показан на рисунке.

Другой можно получить, если перекрасить красные части в жёлтый цвет, а жёлтые – в красный. Видим, что правильным является ответ 3.
Задание 9
|
В четырёх корзинах находятся 1, 4, 6 и 9 яблок. Какое наименьшее количество яблок нужно переместить между корзинами, чтобы в них яблок стало поровну?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 31.5 - 0.75 = 30.75
|
Согласно условию, всего в четырёх корзинах находится
1 + 4 + 6 + 9 = 20 яблок.
Поэтому, если их разложить по корзинам поровну, то в каждой корзине должно оказаться
20 : 4 = 5 яблок.
Для этого, по крайней мере, нужно убрать из третьей корзины
6 – 5 = 1 яблоко
и из четвёртой корзины
9 – 5 = 4 яблока.
Видим, что нужно переложить не менее
1 + 4 = 5 яблок.
С другой стороны, если 1 яблоко из третьей корзины переложить во вторую и 4 яблока из четвёртой корзины – в третью, то во всех корзинах яблок станет поровну. Поэтому правильным является ответ 5.
Задание 10
|
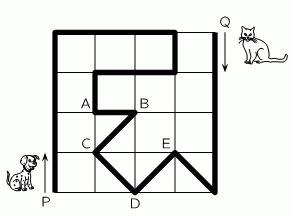
Собака и кошка идут в парке по тропе, отмеченной жирной линией. Они выходят одновременно из точек P и Q соответственно. Собака идёт в три раза быстрее, чем кошка. В какой точке они встретятся?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 30.75 - 0.75 = 30
|
Примем длину стороны клетки за 1. Пока кошка дойдёт до точки F, пройдя расстояние 4, собака пройдёт расстояние 4 · 3 = 12 и окажется в точке В. Далее, пока кошка пройдёт диагональ FE, собака пройдёт 3 диагонали (BC, CD и DE). В результате они встретятся в точке E.
Задание 11
|
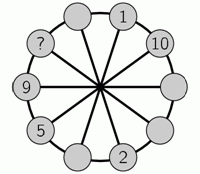
Маша хочет вписать числа от 1 до 10 в кружочки на колесе. Сумма чисел в любых двух соседних кружочках должна быть равна сумме чисел в двух диаметрально противоположных им кружочках (Например, сумма чисел в двух соседних верхних кружочках должна равняться сумме чисел в двух соседних нижних кружочках.). Некоторые числа Маша уже вписала так, как показано на рисунке. Какое число она должна вписать в кружочек со знаком вопроса?
A) 3 Б) 4 В) 6 Г) 7 Д) 8
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 30 - 1 = 29
|

Рассмотрим соседние кружочки с числами 9 и 5, сумма которых равна 14 (см. рис.). Напротив числа 5 находится число 10. Тогда, согласно условию, напротив числа 9 должно быть число 14 – 10 = 4.
Точно так же рассмотрим соседние кружочки с числами 1 и 10, их сумма равна 11. Напротив числа 10 находится число 5. Тогда напротив числа 1 должно быть число 11 – 5 = 6.
Теперь рассмотрим соседние кружочки с числами 6 и 2, их сумма равна 8. Напротив числа 6 находится число 1. Тогда напротив числа 2 должно находиться число 8 – 1 = 7. Оно на 5 больше расположенного напротив него числа 2. Значит, искомое число в кружочке, отмеченном знаком «?», должно быть на 5 меньше числа, расположенного напротив него.
По условию, Маша вписывает в кружочки числа от 1 до 10. На рисунке уже имеются все числа, кроме чисел 3 и 8. Видим, что рядом с числом 7 должно быть вписано число 3, а рядом с числом 2 – число 8. Таким образом, правильным является ответ 3.
Задание 12
|
Когда летучая мышь Лиза вылетела из пещеры, цифровые часы показывали 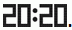 Когда она вернулась, то, вися вниз головой, снова увидела на часах
Когда она вернулась, то, вися вниз головой, снова увидела на часах 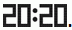 Как долго Лиза находилась вне пещеры?
Как долго Лиза находилась вне пещеры?
A) 3 ч 28 мин
Б) 3 ч 40 мин
В) 3ч 42 мин
Г) 4 ч 18 мин
Д) 5 ч 42 мин
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 29 - 1 = 28
|
Если перевернуть показания часов  , то получим
, то получим  .
.
То есть летучая мышь Лиза вернулась в пещеру в 02:02. Тогда Лиза летала 3 ч 40 мин до полуночи и 2 ч 2 мин после полуночи. Складывая эти промежутки времени, находим, что вне пещеры Лиза находилась 5 ч 42 мин.
Задание 13
|
Встретились эльф и тролль. Тролль всегда лжёт, а эльф всегда говорит правду. Они оба произнесли одно из следующих предложений. Какое?
A) Я говорю правду.
Б) Ты говоришь правду.
В) Мы оба говорим правду.
Г) Я всегда лгу.
Д) Только один из нас говорит правду.
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 28 - 1 = 27
|
Если эльф произнёс «я говорю правду», то это правдивое утверждение, так как он всегда говорит правду. Значит, эльф, действительно, мог произнести это предложение. Если тролль произнёс «я говорю правду», то это ложное утверждение, поскольку тролль всегда лжёт. Значит, тролль тоже мог произнести это предложение. Поскольку, согласно условиям конкурса, среди вариантов ответа только один правильный, им является ответ А.
Хотя правильный ответ уже найден, нетрудно убедиться, что предложения в других вариантах ответа не могли произнести эльф и тролль.
Б) «Ты говоришь правду» не мог произнести ни эльф, ни тролль.
В) «Мы оба говорим правду» не мог произнести эльф.
Г) «Я всегда лгу» не мог произнести ни эльф, ни тролль.
Д) «Только один из нас говорит правду» не мог произнести тролль.
Задание 14
|
У Маши ровно 10 белых кубиков, 9 светло-серых и 8 тёмно-серых, все одного размера. Она склеивает все кубики так, чтобы получился большой куб. Какой из следующих кубов у неё может получиться?

|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 27 - 1 = 26
|
По условию, склеенный Машей куб состоит из 10 белых, 9 серых и 8 чёрных кубиков. Куб в варианте ответа А имеет по крайней мере 10 серых кубиков (5 в верхнем слое, 2 в среднем слое и 3 в нижнем слое). То есть количество серых кубиков у этого куба больше, чем было у Маши. Поэтому ответ А не является правильным. На рисунке в ответе Б мы видим 9 серых кубиков и 10 белых. Поэтому, если все 8 невидимых кубиков являются чёрными, то такой куб мог быть склеен Машей. Следовательно, так как, по условиям конкурса, только один из вариантов ответа правильный, им является ответ Б.
Хотя правильный ответ уже найден, нетрудно убедиться, что все следующие варианты ответа не могут быть правильными. Действительно, в ответе В видно 11 белых кубиков, а у Маши их было только 10. В ответе Г видно 9 чёрных кубиков, а у Маши их было только 8. В ответе Д видно 10 серых кубиков, а у Маши их было только 9.
Задание 15
|
На следующих диаграммах отмечены жирной линией пути от X до Y. Какой из них самый короткий?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 26 + 4 = 30
|
Все пути в вариантах ответа состоят из четвертей окружностей (большой, средней и малой) и отрезков (вертикальных и горизонтальных) одинаковой длины. Для каждого из путей подсчитаем их количества. Результаты подсчётов приведены в таблице.

Сравнивая столбцы этой
таблицы, видим, что самым коротким является путь В.
Задание 16
|
Папа кенгуру живёт со своими тремя детьми. Они решают все вопросы путём голосования, и каждый член семьи имеет право на столько голосов, сколько ему лет. Сейчас папе 36 лет, а детям 13, 6 и 4 года. Поэтому папа всегда побеждает. Сколько лет должно пройти, чтобы дети могли выиграть у папы, если они с ним не согласны?
A) 5 Б) 6 В) 7 Г) 13 Д) 14
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 30 - 1 = 29
|
Согласно условию, сейчас при голосовании папа имеет 36 голосов, а дети
13 + 6 + 4 = 23 голоса.
Разность составляет
36 – 23 = 13 голосов.
С каждым годом число голосов у папы увеличивается на 1, а у детей – на 3. Тем самым, разность в количестве голосов уменьшается на 2.
Так как 13 : 2 = 6,5, а ближайшее целое число, большее 6,5, равно 7, то через 7 лет число голосов у детей впервые станет больше, чем у папы. Таким образом, правильным является ответ 7.
Задание 17
|
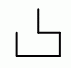
У Жоры есть два одинаковых куска проволоки, показанных на рисунке. Какую из следующих конструкций нельзя получить, спаяв два таких куска?
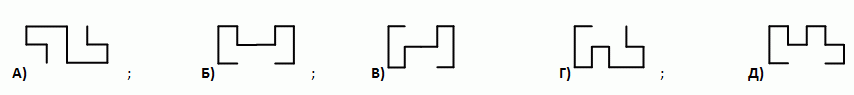
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 29 + 4 = 33
|
Ниже показано, что конструкции в вариантах ответа А) – Г) можно спаять из двух кусков, указанных в условии задачи:

Таким образом, правильным может быть только ответ Д.
Действительно, в конструкции  один из кусков (чёрный) является таким, который указан в условии задачи. Но второй кусок (красный), очевидно, таким не является.
один из кусков (чёрный) является таким, который указан в условии задачи. Но второй кусок (красный), очевидно, таким не является.
Задание 18
|
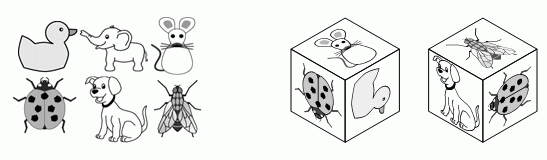
Аня наклеила шесть стикеров на грани кубика. На рисунке показаны эти стикеры и вид кубика с двух сторон. Какой стикер находится на грани, противоположной грани с мышью?
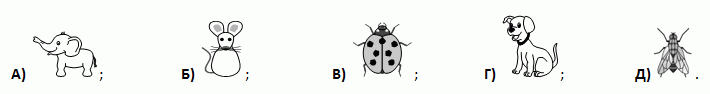
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 33 - 1 = 32
|
На первом изображении кубика божья коровка расположена головой вниз. Чтобы она была ориентирована так же на изображении второго кубика, нужно этот кубик перекатить так, как показано на рисунке.

Видим, что в результате стикер с собачкой окажется на нижней грани. А на верхней грани, как видно на первом изображении кубика, находится стикер мыши. Таким образом, на грани, противоположной грани с мышью, находится собачка.
Задание 19
|
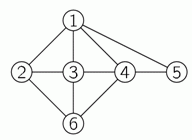
Рисунок показывает дружеские отношения между шестью девочками. Девочек зовут Аня, Бася, Валя, Галя, Дина и Ева. Девочки изображены кружочками с числами. Если какие-то две девочки дружат между собой, то соответствующие кружочки соединены отрезком. Валя, Галя и Ева имеют по 4 подруги. Бася дружит только с Валей и Галей. Каким числом обозначена на рисунке Ева?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 32 + 4 = 36
|

На схеме видно, что ровно две подруги имеет только девочка, изображённая кружочком 5. Значит, согласно условию, это Бася. Кроме того, так как Бася дружит только с Валей и Галей, то, согласно схеме, Валя и Галя обозначены кружочками 1 и 4. Валя и Галя имеют 4 подруги. Ещё, кроме них, по условию, 4 подруги имеет Ева. А на
схеме, кроме девочек 1 и 4 (Вали и Гали), ещё 4 подруги у девочки,
изображённой кружочком 3. Значит, этой девочкой является Ева. Таким образом, правильным является ответ 3.
Задание 20
|
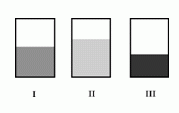
Маша налила одинаковое количество жидкости в три прямоугольных сосуда. Если смотреть на эти сосуды спереди, то кажется, что они имеют одинаковый размер. Но жидкости в них имеют разные уровни. На каком из следующих рисунков показан вид сверху на эти три сосуда?

|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 36 - 1 = 35
|
На рисунке в условии задачи самый высокий уровень жидкости во втором сосуде, а самый низкий – в третьем. Но, по условию, во всех сосудах объём жидкости одинаковый. Следовательно, площадь основания второго сосуда самая маленькая, а площадь основания третьего сосуда самая большая. Размеры основания прямоугольных сосудов такие же, как у их вида сверху. Сравнивая варианты ответа, видим, что основания сосудов обладают нужными свойствами только в ответе А.
Задание 21
|
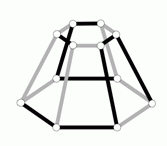
Как выглядит сверху следующая конструкция?

|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 35 - 1.25 = 33.75
|
Рассмотрим на рисунке пирамиды в условии задачи путь наибольшей длины, состоящий из чёрных рёбер (см. рис.).

Будем искать такой же путь на рисунках в вариантах ответа. Видим, что такой путь имеется только в варианте ответа Б. Сравнивая другие элементы рисунка в ответе Б с элементами пирамиды в условии задачи, убеждаемся, что и они идентичны. Таким образом, правильным является ответ Б.
Задание 22
|
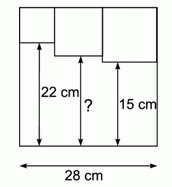
Внутри квадрата расположены три меньших квадрата так, как показано на рисунке. Чему равна длина отрезка, обозначенного знаком вопроса?
A) 17 см Б) 17,5 см В) 18 см Г) 15,5 см Д) 19 см
|
Правильный ответ: Д
|
Ответ участника: А
|
Промежуточный результат: 33.75 - 1.25 = 32.5
|
Так как сторона данного квадрата равна 28 см, то, согласно данным на рисунке в условии задачи, сторона меньшего квадрата в верхнем левом углу равна
28 – 22 = 6 см,
а сторона квадрата в правом верхнем углу равна
28 – 15 = 13 см (см. рис.).

Тогда сторона среднего меньшего
квадрата равна
28 – 6 – 13 = 9 см.
Поэтому искомая длина равна
28 – 9 = 19 см.
Задание 23
|
Будем называть трёхзначное число красивым, если его средняя цифра больше суммы его первой и последней цифры. Какое наибольшее количество последовательных трёхзначных чисел могут оказаться красивыми?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 32.5 - 1.25 = 31.25
|
Трёхзначное число не может начинаться цифрой 0. Поэтому первая цифра красивого числа не меньше 1. Последняя цифра красивого числа не может быть 8 или 9, иначе средняя цифра, согласно определению красивого числа, должна быть больше
1 + 8 = 9,
а таких цифр не существует. Следовательно, существует не более 8 возможных значений для последней цифры красивого числа: 0, 1, 2, 3, 4, 5, 6 и 7. Причём, если мы рассматриваем цепочку последовательных красивых чисел, то ни одна из этих цифр не может быть в такой цепочке последней дважды. Действительно, в противном случае таких чисел было бы не менее 11 (два с совпадающими последними цифрами и ещё 9 чисел между ними). Но тогда были бы числа с последней цифрой 8 и последней цифрой 9. Противоречие. Таким образом, последовательных красивых чисел не может быть более восьми. А восемь последовательных красивых чисел есть: 190, 191, 192, 193, 194, 195, 196, 197. Видим, что правильным является ответ 8.
Задание 24
|
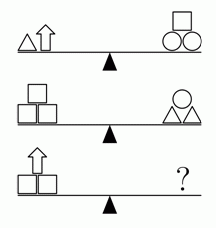
Какой из следующих наборов уравновесит третьи весы?
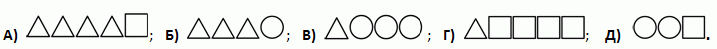
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 31.25 - 1.25 = 30
|
Поместим на одну чашу весов всё, что находится на левых чашах двух весов в условии задачи, а на другую – всё, что находится на правых чашах. Согласно условию, получим баланс (чаши будут уравновешены; см. рис.1).

После этого уберём с обеих чаш одинаковые предметы (треугольник и квадрат). Видим (см. рис.2), что правильным является ответ В.
Задание 25
|
Десять школьников заказали по одному шарику мороженого: 4 ванильного, 3 шоколадного, 2 лимонного и 1 манго. Они добавили к мороженому 4 зонтика, 3 вишенки, 2 вафли и 1 клубничку, к каждому шарику что-то ровно одно, так, что все десять сочетаний оказались различным. Какое из следующих сочетаний не могло получиться?
A) шоколадное с вишней
Б) манго с зонтиком
В) ванильное с зонтиком
Г) лимонное с вафлей
Д) ванильное с клубничкой
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 30 - 1.25 = 28.75
|
По условию, школьники заказали 4 порции ванильного мороженого и добавки к ним были разного вида из четырёх возможных. Значит, было ванильное мороженое с зонтиком, ванильное мороженое с вишней, ванильное мороженое с вафлей и ванильное мороженое с клубничкой. Уже видим, что ответы В и Д не являются верными.
Далее, на остальные мороженые (3 шоколадных, 2 лимонных и 1 манго) остаются в качестве добавок 3 зонтика, 2 вишни и 1 вафля. Так как, по условию, и шоколадные мороженые были с разными добавками, то одно шоколадное мороженое было с зонтиком, одно с вишней и одно с вафлей. Стало быть, и ответ А не является верным.
Наконец, на оставшиеся порции мороженого (2 лимонных и 1 манго) остаются в качестве добавок 2 зонтика и 1 вишня. Все лимонные мороженые тоже были с разными добавками. Поэтому было лимонное
мороженое с зонтиком, лимонное мороженое с вишней, и последнее мороженое манго было с зонтиком. Видим, что лимонного мороженого с вафлей не было. Поэтому верный ответ – это ответ Г.
Задание 26
|

У Вани есть 9 жетонов, с одной стороны они белые, а с другой – чёрные. Изначально жетоны выложены в ряд так, как показано на рисунке. За один ход Ваня может перевернуть любые 3 жетона. За какое наименьшее количество ходов Ваня может добиться того, чтобы сверху все жетоны были одного цвета?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 28.75 - 1.25 = 27.5
|
Так как за один ход Ваня может перевернуть ровно 3 жетона, то после одного хода все жетоны не могут быть одного и того же цвета сверху. А двух ходов для этого достаточно (см. рис.).

Задание 27
|
Магнус должен сыграть 15 партий в шахматном турнире. В какой-то момент времени из сыгранных партий он имел половину выигрышей, треть проигрышей и 2 ничьих. Сколько партий ещё оставалось сыграть Магнусу?
A) 2 Б) 3 В) 4 Г) 5 Д) 6
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 27.5 - 1.25 = 26.25
|
На тот момент, когда Магнус имел половину выигрышей, треть проигрышей и 2 ничьих, число сыгранных партий должно делиться на 2 и на 3, а значит, делиться на 6. Следовательно, к этому моменту было сыграно 6 или 12 партий (их не могло быть больше 15). Если было сыграно только 6 партий, то, согласно условию, среди них было
6 : 2 = 3 выигрыша, 6 : 3 = 2 проигрыша и тогда число ничьих равно
6 – 3 – 2 = 1. Противоречие: по условию, было 2 ничьих.
Видим, что к указанному моменту могло быть сыграно 12 партий. Легко убедиться, что в этом случае все условия задачи выполняются. Значит, после указанного момента Магнусу ещё оставалось сыграть
15 – 12 = 3 партии.
По-другому найти правильный ответ можно было так. В рассматриваемый момент времени у Магнуса было
1/2 + 1/3 = 5/6 результативных партий (побед и проигрышей) из сыгранных к данному моменту. Значит, 1/6 партий было сыграно вничью. По условию, это составляет 2 партии. Тогда всего к данному моменту было сыграно
2 · 6 = 12 партий и оставалось сыграть ещё
15 – 12 = 3 партии.
Задачу можно легко решить с помощью уравнений. Пусть x – число партий, сыгранных Магнусом к рассматриваемому моменту времени. Тогда, согласно условию,
x/2 + x/3 + 2 = x, откуда х = 12 и, значит, правильный ответ
15 – 12 = 3.
Задание 28
|
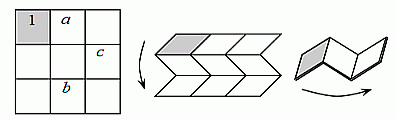
У Вадима имеется квадратный лист бумаги, состоящий из 9 клеток. Он хочет сложить его по линиям клеток сначала по горизонтали, а затем по вертикали, так чтобы серая клетка оказалась сверху (см. рис.). Вадим хочет вписать в клетки числа от 1 до 9 так, чтобы после сгиба квадрата числа в клетках располагались (сверху вниз) в порядке возрастания. Какие числа он должен вписать вместо букв а, b и c?
A) a = 6, b = 4, c = 8
Б) a = 4, b = 6, c = 8
В) a = 5, b = 7, c = 9
Г) a = 4, b = 5, c = 7
Д) a = 6, b = 4, c = 7
|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 26.25 - 1.25 = 25
|
После первого сворачивания клетки каждого столбца сложатся так, что верхние клетки останутся верхними, а нижние – нижними. Но после второго сворачивания клетки второго столбца поменяют своё расположение на обратное. Это значит, что в стопке клеток среднего столбца нижняя клетка с числом b окажется сверху, а верхняя с числом a – снизу. В стопке клеток первого и третьего столбцов расположение клеток (сверху вниз) не изменится. При этом три верхние клетки будут клетками первого столбца, следующие три клетки – клетками второго столбца, а последние три клетки – клетками третьего столбца. Следовательно, чтобы после сгибания квадрата числа в клетках располагались (сверху вниз) в порядке возрастания, нужно их вписать так, как показано на рисунке.

В частности, получаем: a = 6, b = 4, c = 8. Таким образом, правильным является ответ А.
В заключение следует заметить, что после сворачивания при просмотре клеток (сверху вниз) число 5 окажется перевёрнутым, а числа 2, 4, 6 и 8 – перевёрнутыми и расположенными на обратной стороне клетки.
Задание 29
|
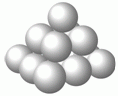
Дима строит пирамиду из одинаковых шариков. Нижний слой представляет собой квадрат из 9 шариков, средний – квадрат из 4 шариков, верхний – 1 шарик. Дима поместил по капле клея во все точки соприкосновения шариков. Сколько таких капель получилось?
A) 20 Б) 24 В) 28 Г) 32 Д) 36
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 25 - 1.25 = 23.75
|
В нижнем слое пирамиды имеется 12 точек соприкосновения шариков: по две в каждом горизонтальном ряду шариков и по две в каждом вертикальном ряду (см рис.).

В среднем слое, состоящем из четырёх шариков, имеется 4 точки их соприкосновения между собой. Далее, каждый из шариков среднего слоя соприкасается с 4 шариками нижнего слоя (всего имеем 4 · 4 = 16 таких точек соприкосновения) и по одному соприкосновению с верхним шариком пирамиды (ещё 4 точки соприкосновения). Всего получаем
12 + 4 + 16 + 4 = 36 точек соприкосновения.
Значит, всего Дима поместил в точки соприкосновения шариков 36 капель клея.
Задание 30
|
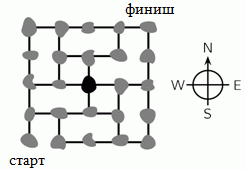
На рисунке показана карта нескольких островов и мостов между ними. Почтальон должен посетить каждый остров ровно один раз. Он начинает путь с острова с пометкой «старт» и хотел бы закончить его на острове с пометкой «финиш». Он только что достиг чёрного острова в центре карты. В каком направлении ему следует двигаться, чтобы завершить свой путь так, как он задумал?
A) на север
Б) на восток
В) на юг
Г) на запад
Д) такого направления не существует
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 23.75 + 5 = 28.75
|
Рассмотрим те острова, которые связаны с другими ровно двумя мостами. Ясно, что если этот остров – не «старт» и не «финиш», то почтальон должен проехать по обоим этим мостам. Иначе он не сможет въехать или выехать с такого острова. Отметим на карте все такие мосты зелёной линией (см. рис.1). Это даёт нам некоторые части искомого пути почтальона.

Далее, если через какой-то остров уже проходит построенная часть пути, то другие мосты, не отмеченные на этом пути, можно исключить из рассмотрения. Действительно, для каждого промежуточного острова существует только два моста на искомом пути (один, по которому почтальон въезжает на остров, и один, по которому он уезжает с острова). Удалим такие мосты на рисунке (см. рис.2). После этого появляются другие острова, из которых выходят только два моста, и путь можно достроить по таким же соображениям, как вначале (см. рис.3). Теперь легко завершишь построение пути от «старта» к «финишу» (см. рис.4). Видим, что такой путь единственный и через центральный остров он проходит слева направо, т.е. в направлении на восток.

















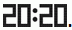 Когда она вернулась, то, вися вниз головой, снова увидела на часах
Когда она вернулась, то, вися вниз головой, снова увидела на часах  , то получим
, то получим  .
.


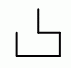
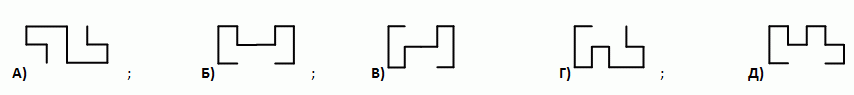

 один из кусков (чёрный) является таким, который указан в условии задачи. Но второй кусок (красный), очевидно, таким не является.
один из кусков (чёрный) является таким, который указан в условии задачи. Но второй кусок (красный), очевидно, таким не является.