Задание 1
|
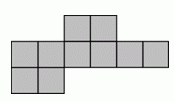
Фигура на рисунке состоит из клеток со стороной 1 см. Чему равен её периметр?
A) 14 см Б) 18 см В) 30 см Г) 32 см Д) 40 см
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 30 - 0.75 = 29.25
|
Периметр данной фигуры можно подсчитать непосредственно, складывая длины всех сторон. В результате получим 18 см.
Можно заметить также, что он равен периметру прямоугольника 6 х 3 (см. рис.).

Задание 2
|
Если значения следующих выражений расположить в порядке возрастания, то какое будет средним?
A) 1 + 2345
Б) 12 + 345
В) 123 + 45
Г) 1234 + 5
Д) 12345
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 29.25 + 3 = 32.25
|
Имеем:
А) 1 + 2345 = 2346,
Б) 12 + 345 = 357,
В) 123 + 45 = 168,
Г) 1234 + 5 = 1239,
Д) 12345.
Видим, что средним является выражение Г.
Задание 3
|
Чему равна сумма двух последних цифр произведения
1 • 2 • 3 • 4 • 5 • 4 • 3 • 2 • 1?
A) 2 Б) 4 В) 6 Г) 8 Д) 16
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 32.25 + 3 = 35.25
|
Поскольку 2 · 5 = 10, то последняя цифра данного в условии произведения равна 0, а предпоследняя цифра – это последняя цифра произведения
3 · 4 · 4 · 3 · 2 = 12 · 24.
Последняя цифра этого произведения – такая же, как у произведения последних цифр множителей, и равна 2 · 4 = 8. Следовательно, сумма двух последних цифр произведения из условия задачи равна 8 + 0 = 8.
Задание 4
|
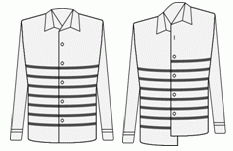
Когда Коля надевает свою новую рубашку правильно, как показано на левом рисунке, то горизонтальные полосы образуют семь замкнутых колец вокруг его талии. Этим утром он неправильно застегнул пуговицы, как показано на правом рисунке. Сколько замкнутых колец получилось вокруг талии Коли в этот раз?
A) 0 Б) 1 В) 2 Г) 3 Д) 4
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|
После того как Коля неправильно застегнул пуговицы, кольца на рубашке образовали одну непрерывную спираль (см. рис.). Ни одного кольца в результате не образовалось.

Задание 5
|
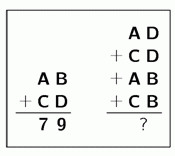
В приведённых вычислениях одинаковые буквы обозначают одинаковые цифры, а разные буквы – разные числа. Сумма двух чисел справа равна 79. Чему равна сумма четырёх чисел?
A) 79 Б) 158 В) 869 Г) 1418 Д) 7979
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Из условия следует, что
10(А + С) + (B + D) = 79.
Вторая сумма на рисунке в условии равна
20(A + C) + 2(B + D),
т. е. в два раза больше первой суммы и, значит, равна
2 · 79 = 158.
Задание 6
|
Сумма четырёх последовательных целых чисел равна 2. Чему равно наименьшее из этих чисел?
A) -3 Б) -2 В) -1 Г) 0 Д) 1
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 41.25 + 3 = 44.25
|
Пусть наименьшее из данных четырёх чисел равно x. Тогда сумма этих чисел равна
x + (x + 1) + (x + 2) + (x + 3) = 4x + 6.
Согласно условию, 4x + 6 = 2, откуда x = –1.
Задание 7
|
Годы 2020 и 1717 состоят из двух повторяющихся двухзначных чисел. Через какое наименьшее число лет после 2020 года наступит год с таким же свойством?
A) 20 Б) 101 В) 120 Г) 121 Д) 202
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 44.25 + 3 = 47.25
|
Год 2020 состоит из двух повторяющихся чисел 20. Следующим натуральным числом после числа 20 является число 21. Поэтому следующим годом после 2020, состоящим из двух повторяющихся чисел, является год 2121. Он наступит через
2121 – 2020 = 101 год.
Задание 8
|
У Мэри было несколько бумажных фигур: некоторые из них – квадраты, а остальные – треугольники. Она разрезала 3 квадрата по диагонали, и у неё получилось 13 фигур, имеющих 42 вершины. Сколько треугольников выло у Мэри до того, как она сделала разрезы?
A) 8 Б) 7 В) 6 Г) 5 Д) 4
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 47.25 + 3 = 50.25
|
По условию, 13 фигур (треугольников и квадратов) имеют 42 вершины. Если бы все фигуры были треугольниками, то у них было бы 13 · 3 = 39 вершин. Квадрат имеет на одну вершину больше, чем треугольник. Поэтому превышение на 42 – 39 = 3 вершины имеет место из-за того, что среди фигур есть 3 квадрата. Так как до этого на треугольники были
разрезаны 3 квадрата, то вначале их было 3 + 3 = 6. Заметим также, что после разрезания каждого квадрата на 2 треугольника
число фигур увеличивается на 1. Поэтому вначале было 13 – 3 = 10 фигур и, значит, среди них было 10 – 6 = 4 треугольника.
По-другому задачу можно было решить так. Пусть вначале было x треугольников. После разрезания 3 квадратов из каждого квадрата получилось 2 треугольника, вследствие чего число треугольников увеличилось на 3 · 2 = 6 и их стало x + 6. Тогда квадратов среди образовавшихся фигур стало
13 – (x + 6) = 7 – x.
По условию, число вершин у образовавшихся фигур равно 42. Имеем:
3(x + 6) + 4(x – 7) = 42, или 46 – x = 42, откуда x = 4.
Задание 9
|
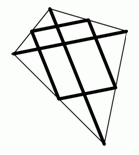
Мартин изготовил воздушного змея (см. рис.). Для этого он взял прямую деревянную планку и разрезал её на 6 частей. Две из них, длины 120 см и 80 см, он использовал как диагонали. Остальными четырьмя частями он соединил середины стороны воздушного змея. Какой длины была планка до того, как её разрезали?
A) 300 см Б) 370 см В) 400 см Г) 410 см Д) 450 см
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 50.25 + 3 = 53.25
|
Обозначим вершины змея и середины его сторон так, как показано на рисунке.

Согласно условию, меньшая диагональ AC = 80 см, а большая BD = 120. Далее, отрезки KL и NM являются средними линиями треугольников ABC и ACD соответственно, параллельными основанию AC. Поэтому
KL = NM = AC : 2 = 80 : 2 = 40 см.
Аналогично,
KN = LM = BD : 2 = 120 : 2 = 60.
Тогда длина планки, использованной для изготовления змея, равнялась
80 + 40 + 40 + 120 + 60 + 60 = 400 см.
Задание 10
|

На клетчатой бумаге со стороной клетки 1 отмечены четыре точки, как показано на рисунке. Какую наименьшую площадь может иметь треугольник с вершинами в каких-то трёх из отмеченных точек?
A) 1/2 Б) 1 В) 3/2 Г) 2 Д) 5/2
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 53.25 - 0.75 = 52.5
|
Всего можно построить 4 треугольника с вершинами в отмеченных точках. Нарисовав каждый из них, мы уже по рисункам видим, что наименьшую площадь имеет тот треугольник, который показан на рисунке ниже.

Вообще, у каждого треугольника с вершинами в узлах сетки можно указать сторону и проведённую к ней высоту, которые имеют длину не меньше 1. Поэтому площадь любого треугольника с вершинами в узлах сетки не меньше 1/2. Изображённый на рисунке треугольник как раз имеет такую площадь. Поэтому правильным является ответ А.
Задание 11
|
Елена хочет провести 18 дней подряд в гостях у бабушки. Её бабушка рассказывает ей интересные истории по вторникам, субботам и воскресеньям. Елена хочет услышать как можно больше бабушкиных историй. В какой день недели ей для этого нужно приехать?
A) в понедельник
Б) во вторник
В) в пятницу
Г) в субботу
Д) в воскресенье
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 52.5 + 4 = 56.5
|
18 дней включают две полные недели (их можно отсчитывать со дня приезда Елены) и ещё 4 дня третьей недели. Поэтому Елена услышит наибольшее количество бабушкиных историй, если на эти последние 4 дня придётся наибольшее число дней, которые являются вторником, субботой и воскресеньем. Понятно, что таких дней среди 4 подряд идущих дней не более 3. Но если Елена приедет в субботу, то их как раз и будет 3. А если она приедет в другой день, то таких дней будет меньше. Поэтому правильным является ответ Г.
Задание 12
|
Целые числа a, b, c и d удовлетворяют равенству ab = 2cd. Какое из следующих чисел не может быть значением произведения abcd ?
A) 50 Б) 100 В) 200 Г) 450 Д) 800
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 56.5 - 1 = 55.5
|
Из равенства ab = 2cd следует, что abcd = 2(ab)2, т.е. произведение abcd является удвоенным квадратом некоторого числа. Разделив на 2 числа в вариантах ответа, получим:
А) 25, Б) 50, В) 100, Г) 225, Д) 400
Видим, что только в варианте ответа Б число не является полным квадратом. Примеры значений a, b, c и d для других вариантов ответа легко подобрать. Таким образом, правильным является ответ 100.
Задание 13
|
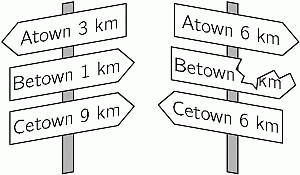
Кратчайший путь от Атауна до Цетауна пролегает через Бетаун. На этом пути сначала встречается левый указатель, а затем – правый (см. рис.). Какое расстояние было написано на сломанном знаке?
A) 1 км Б) 2 км В) 3 км Г) 4 км Д) 5 км
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 55.5
Из данных на первом указателе следует, что расстояния между Атауном и Бетауном равно 3 + 1 = 4 км, а расстояние между Бетауном и Цетауном равно 9 – 1 = 8 км (см. рис.)

Поэтому видим, что, согласно данным на втором указателе, расстояние от него до Бетауна равно 8 – 6 = 2 км. Поэтому правильным является ответ 2.
Заметим в заключение, что если ехать по дороге от Атауна до Цетауна, то первый указатель должен быть расположен на левой стороне дороги, в второй – на правой. Кроме того, в условии данной задачи, как и в условии аналогичной задачи №11 для 7-8 классов, имеются лишние данные. Ответ можно найти без сведений о расстоянии до Цетауна на обоих указателях.
|
Задание 14
|
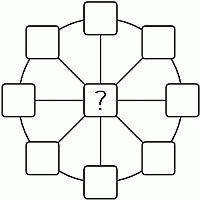
Том вписывает числа во все девять ячеек на рисунке. Он хочет, чтобы суммы трёх чисел на каждом диаметре были равны 13, а сумма всех восьми чисел на окружности равнялась 40. Какое число Том должен вписать в центральную ячейку?
A) 3 Б) 5 В) 8 Г) 10 Д) 12
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 55.5
Сложим суммы чисел на четырёх диагоналях. С одной стороны, получим 4 · 13 = 52, так как сумма чисел на каждой диагонали равна 13. С другой стороны, если x – число в центре, то найденная сумма равна 40 + 4х, так как сумма чисел на окружности равна 40 и x входит как слагаемое в каждую из четырёх сумм на диагоналях. Имеем: 40 – 4х = 52, откуда х = 3.
Пример для чисел на окружности не обязателен. Но таких примеров существует бесконечно много. Достаточно на концах каждой диагонали вписать любые два числа, сумма которых равна 10.
|
Задание 15
|
Одна из сторон равнобедренного треугольника имеет длину 20 см. Длины двух других сторон относятся как 2 : 5. Какой периметр имеет этот треугольник?
A) 36 см Б) 48 см В) 60 см Г) 90 см Д) 120 см
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 55.5 + 4 = 59.5
|
По условию, длина одной из сторон данного треугольника равна 20 см, а длины двух других сторон равны 20х см и 50х см при некотором x. Так как треугольник равнобедренный, то либо 20х = 20, либо 50х = 20. В первом случае стороны треугольника (в см) равны 20, 20 и 50. Но такого треугольника не существует, так как одна из сторон оказывается больше суммы двух других, что невозможно. Во втором случае стороны треугольника равны 20, 20 и 8. Такой треугольник действительно существует, и его периметр равен
20 + 20 + 8 = 48 см.
Задание 16
|
Маша поставила знак умножения между 2-й и 3-й цифрами числа 2020 и заметила, что полученное произведение 20 • 20 является полным квадратом. Сколько всего чисел от 2010 до 2099 обладают таким же свойством?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 59.5 - 1 = 58.5
|
Задача состоит в том, чтобы найти числа вида 20A, где A – двузначное число,
20 ≤ А ≤ 100, и такое, что
20А = n2 для некоторого натурального n.
Из последнего равенства следует, что n = 10m для некоторого натурального m. Тогда
A/5 = m2 и
4 ≤ A/5 = m2 < 20.
Только три числа m = 2, 3 и 4 удовлетворяют полученным ограничениям. Поэтому правильным является ответ 3.
Нетрудно подсчитать, что искомыми тремя числами в пределах от 2020 до 2099 включительно являются числа 2020, 2045
и 2080.
Задание 17
|
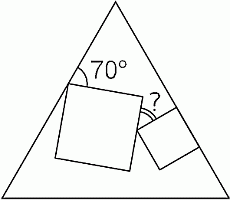
Внутри равностороннего треугольника находятся два квадрата разного размера. Одна из сторон меньшего квадрата лежит на одной из сторон треугольника, как показано на рисунке. Чему равна величина угла, отмеченного знаком вопроса?
A) 25° Б) 30° В) 35° Г) 45° Д) 50°
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 58.5 - 1 = 57.5
|
В верхней части данного треугольника (см. рис. в условии задачи) находится невыпуклый пятиугольник KLTPN. Все его углы, кроме искомого, понятны из условия задачи. Их значения равны 60°, 70°, 270° и 90°. А поскольку сумма углов любого пятиугольника равна 540°, то величина искомого угла равна
540° – 60° – 70° – 270° – 90 = 50°.
Правильный ответ можно найти и другими способами. Например, так. Продлим одну из сторон большего квадрата так, как показано на рисунке.

В полученном четырёхугольнике KLMN находим:
∠LMN = 360° – 60° – 70° – 90° = 140°.
Тогда в треугольнике MPT смежный угол ∠NMT равен
180° – 140° = 40° и, значит, искомый угол
∠MNT равен 90° – 40° = 50°.
Задание 18
|
Макар отправился в 520-километровую поездку. В топливном баке ёмкостью 40 литров было 14 литров топлива. Автомобиль Макара потребляет 1 литр топлива на 10 км. Проехав 55 км, Макар увидел дорожный знак, показывающий расстояния до ближайших автозаправочных станций впереди по дороге. Эти расстояния равны 35 км, 45 км, 55 км, 75 км и 95 км. Макар хочет только один раз остановиться для дозаправки. На каком расстоянии находится нужная автозаправочная станция?
A) 35 км Б) 45 км В) 55 км Г) 75 км Д) 95 км
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 57.5 - 1 = 56.5
|
Так как Макар проехал 55 км, то заправочные станции, о которых идёт речь, находятся от места старта на расстояниях
35 + 55 = 90 км,
45 + 55 = 100 км,
55 + 55 = 110 км,
75 + 55 = 130 км и
95 + 55 = 150 км соответственно.
Согласно условию, бензина в баке было на 14 · 10 = 140 км. Поэтому Макар на имеющемся топливе не может доехать до последнего из указанных пунктов заправки, но сможет доехать до остальных четырёх пунктов.
От четвёртого пункта заправки Макару останется ещё ехать 520 – 130 = 390 км. Поэтому, если он зальёт в этом пункте полный
бак топлива, то, по условию, сможет проехать ещё 40 · 10 = 400 км, чего достаточно для завершения поездки без второй дозаправки.
Если же Макар заправит полный бак раньше, то без ещё одной заправки сможет проехать от старта не более 110 + 400 = 510 км, чего недостаточно для завершения поездки. Таким образом, правильным является ответ 75 км.
Задание 19
|
Если 17x + 51y = 102, то чему равно значение 9x + 27y?
A) 54 Б) 36 В) 34 Г) 18 Д) невозможно определить
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 56.5 + 4 = 60.5
|
Сначала разделим обе части уравнения
17x + 51y = 102 на 17.
Получим: x + 3y = 6.
Затем умножим обе части этого уравнения на 9. Получим:
9x + 27y = 54.
Видим, что правильным является ответ 54.
По-другому ответ можно было получить так. Выразим из данного уравнения x через y. Получим:
x = 6 – 3y.
Подставим в выражение, значение которого нужно найти:
9x + 27y = 9(6 – 3y) + 27y = 54.
Задание 20
|
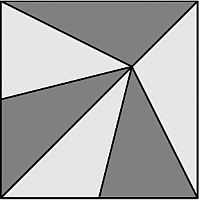
Витраж квадратной формы площади 81 дм2 состоит из шести равновеликих треугольников (см. рис.). В общей вершине всех этих треугольников сидит муха. На какой высоте от нижнего края витража она находится?
A) 3 дм Б) 5 дм В) 5,5 дм Г) 6 дм Д) 7,5 дм
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 60.5
Так как, по условию, площадь данного квадрата равна 81 дм2, его сторона равна 9 дм. Поскольку квадрат состоит из 6 равновеликих треугольников, то площадь каждого из них равна
81 : 6 = 13,5 дм2.
Тогда, рассматривая верхний из треугольников (см. рис.),

получаем 0,5 · 9 · x = 13,5, откуда x = 3 и, значит, y = 9 – 3 = 6.
По-другому найти ответ можно было так. Снова начнём с того, что сторона квадрата равна 9 дм. Далее заметим, что два равновеликих треугольника с основаниями на нижней стороне квадрата имеют равные площади и общую высоту y. Поэтому основания этих треугольников равны между собой и, значит, равны половине стороны квадрата. А основанием верхнего треугольника является вся сторона квадрата, т.е. в 2 раза больше, чем основания нижних треугольников. Поэтому высота x в 2 раза меньше высоты y. Тогда, учитывая, что x + y = 9, находим: x = 3 и y = 6.
|
Задание 21
|
Цифры от 1 до 9 располагаются случайным образом, образуя 9-значное число. Какова вероятность того, что полученное число делится на 18?
A) 1/2 Б) 4/9 В) 5/9 Г) 1/3 Д) 3/4
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 60.5
У любого числа, составленного из цифр от 1 до 9, взятых по одному разу, сумма цифр, равная
1 + 2 + 3 + ... + 9 = 45, делится на 9. Значит, по признаку делимости, и число делится на 9. Чтобы оно делилось на 18, необходимо и достаточно, чтобы оно ещё делилось на 2. А для этого нужно, чтобы его последняя цифра была чётной. Из девяти данных цифр чётными являются четыре цифры. Поэтому искомая вероятность равна 4/9.
|
Задание 22
|
Заяц и Черепаха соревновались в гонке на 5 км по прямой. Скорость Зайца в 5 раз больше скорости Черепахи. Они стартовали одновременно, но Заяц по ошибке побежал перпендикулярно нужному направлению. Через некоторое время он понял свою ошибку, повернул и побежал по прямой к финишу. В результате он прибыл к финишу одновременно с Черепахой. Каково расстояние между точкой поворота Зайца и точкой финиша?
A) 11 км Б) 12 км В) 13 км Г) 14 км Д) 15 км
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 60.5
Согласно условию, траектории движения черепахи и зайца от старта к финишу образуют прямоугольный треугольник (см. рис.).

Кроме того, путь черепахи SF равен
5 км, а путь зайца равен
SP + PF = 5 · 5 = 25 км.
Пусть SP = x. Тогда, по теореме Пифагора,
x2 + 52 = (25 – x)2, или
x2 + 25 = 625 – 50x + x2, или
50x = 600, откуда x = 12. В результате
PF = 25 – 12 = 13 км.
|
Задание 23
|
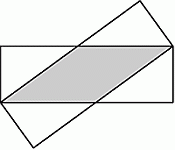
Два одинаковых прямоугольника со сторонами 3 см и 9 см расположены так, как показано на рисунке. Чему равна площадь фигуры, по которой они перекрываются?
A) 12 см2 Б) 13,5 см2 В) 14 см2 Г) 15 см2 Д) 16 см2
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 60.5 - 1.25 = 59.25
|
Пусть ABCD и AECK – два данных прямоугольника (см. рис.1).

Заметим, что треугольники AKL и LCD равны
(AK = CD = 3 см, ∠AKL = ∠LCD = 90° и ∠ALK = ∠CLD, как вертикальные). Обозначим AL = LC = x. Тогда
LD = AD – AL = 9 – x см.
По теореме Пифагора для треугольника
LCD получаем
(9 – x)2 + 32 = x2, или
90 – 18x = 0, откуда x = 5. Тогда искомая площадь параллелограмма ANCL равна
AL · CD = 5 · 3 = 15 см2.
По-другому решить эту задачу можно так. Как показано выше, AL = LC. Поэтому параллелограмм ANCL, площадь которого нужно найти, является ромбом (см. рис.2). Тогда его диагонали AC и NL
пересекаются под прямым углом. По теореме Пифагора для треугольника ACD находим

Далее, заметим, что прямоугольные треугольники ATL и ACD подобны (угол
при вершине A у них общий) с коэффициентом подобия

Тогда
 ,
,
и в результате
 .
.
Задание 24
|
На столе находятся несколько квадратов и треугольников. Некоторые из них синие, а остальные красные. Некоторые из этих фигур большие, а остальные маленькие. Известно, что справедливы следующие два утверждения:
1) если фигура большая, то это квадрат:
2) если цвет фигуры синий, то это треугольник.
Какое из следующих утверждений верно?
A) все красные фигуры являются квадратами
Б) все квадраты большие
В) все маленькие фигуры синие
Г) все треугольники синие
Д) все синие фигуры маленькие
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 59.25
Изобразим ситуацию, описанную в условии задачи, с помощью диаграммы Эйлера-Венна. Пусть круг T – множество треугольников, а круг K – множество квадратов. Эти круги не пересекаются, поскольку квадрат не может быть треугольником.

Далее, согласно условию 1) множество Б (больших фигур) содержится внутри множества K. А согласно условию 2) множество С (синих фигур) содержится внутри множества T (см. рис.). Видим, что, кроме больших квадратов, могут быть маленькие квадраты и, значит, утверждение Б), вообще говоря, неверное. Кроме того, и утверждение А), вообще говоря, неверное, поскольку могут быть не синие треугольники.
Далее, поскольку, кроме синих треугольников, могут быть красные, то и утверждение Г), вообще говоря, неверно. Наконец, из диаграммы видно, что все синие фигуры не являются большими, но могут быть маленькие красные фигуры. Поэтому заведомо
верно утверждение Д) и, вообще говоря, неверно утверждение В).
|
Задание 25
|
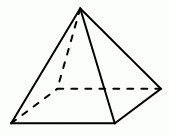
Кенга пронумеровал вершины четырёхугольной пирамиды числами 1, 2, 3, 4 и 5. Затем для каждой грани Кенга вычислил сумму чисел в вершинах данной грани. Четыре из этих сумм оказались равны 7, 8, 9 и 10. Чему равна сумма чисел в вершинах пятой грани?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 59.25 + 5 = 64.25
|
В основании пирамиды находятся 4 вершины. Поэтому сумма чисел на основании не меньше
1 + 2 + 3 + 4 = 10.
Следовательно, если бы одна из этих сумм (а это может быть только сумма 10) действительно была суммой чисел на основании, то в вершине пирамиды было бы записано число 5. А тогда все числа на боковых гранях были бы не меньше
1 + 2 + 5 = 8.
Но, по условию, среди сумм есть сумма 7. Противоречие. Значит, 7, 8, 9 и 10 – суммы чисел на боковых гранях. Если сложить все эти суммы, то каждое число в вершинах нижней грани будет подсчитано дважды, а число в вершине пирамиды будет подсчитано 4 раза. Следовательно,
7 + 8 + 9 + 10 = 2 · (1 + 2 + 3 + 4 + 5) + 2x,
где x – число в вершине пирамиды. Полученное уравнение равносильно
34 = 30 + 2x, откуда x = 2.
Поэтому сумма чисел на основании равна
1 + 3 + 4 + 5 = 13.

Хотя для решения это не требуется, на рисунке показан вид пирамиды сверху с распределением чисел по вершинам и суммами чисел на боковых гранях.
По-другому ответ можно было найти так. Существует только один способ получить на грани сумму 7, а именно
7 = 1 + 2 + 4.
Поэтому сумма 7 – это сумма чисел одной из боковых граней. Тогда одно из чисел 1, 2 или 4 записано в вершине пирамиды, а два других – в вершинах ребра на основании. В вершинах противоположного ребра на основании записаны числа 3, 5, не входящие в сумму
7 = 1 + 2 + 4.
В частности, получаем, что сумма чисел на основании пирамиды не меньше
(3 + 5) + 1 + 2 = 11.
Поэтому все суммы 7, 8, 9, 10 – суммы чисел на боковых гранях.
Далее, заметим, что если сложить две суммы на противоположных боковых гранях, то получится такой же результат, как
если бы мы сложили суммы на двух других противоположных гранях. Действительно, в обоих случаях мы получим сумму всех чисел на основании пирамиды и числа в вершине пирамиды, взятого дважды. В нашем случае есть только один способ разбить числа 7, 8, 9, 10 на пары с одинаковыми суммами:
7 + 10 = 8 + 9.
Отсюда следует, что 8 и 9 – суммы чисел на противоположных боковых гранях и поэтому имеют только одно общее слагаемое в вершине пирамиды. Существует ровно два возможных способа получить сумму
8 = 1 + 2 + 5 = 1 + 3 + 4
и два способа получить сумму
9 = 1 + 3 + 5 = 2 + 3 + 4.
Среди них единственной парой, которая имеет ровно одно общее слагаемое, является
8 = 1 + 2 + 5 и 9 = 2 + 3 + 4.
Этим общим слагаемым является число 2. Следовательно, именно оно записано в вершине пирамиды, и поэтому сумма чисел на основании равна
1 + 2 + 3 + 4 = 13.
Задание 26
|
Большой куб построен из 64 меньших одинаковых кубиков. Три из граней большого куба окрасили. Какое наибольшее количество маленьких кубиков может иметь ровно одну окрашенную грань?
A) 27 Б) 28 В) 32 Г) 34 Д) 40
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 64.25
Ясно, что построенный куб имеет размеры 4 х 4 х 4. Существует только два способа взаимного расположения трёх окрашенных граней куба: либо эти три грани имеют общую вершину, либо не имеют её, и тогда две из граней являются противоположными. В первом случае на каждой из трёх окрашенных граней будет по 9 кубиков, у которых только одна грань окрашена (светло-серая на рис.1).

Всего имеем 3 · 9 = 27 таких кубиков. Во втором случае, для определённости, будем считать окрашенными левую, правую и верхнюю грани (см. рис.2). Видим, что на верней грани куба 8 кубиков имеют ровно одну окрашенную грань (светло-серая).
На правой грани 12 таких кубиков. Ясно, что их столько же и на левой грани. Всего получаем
8 + 12 + 12 = 32 кубика. Это больше, чем в первом случае, и, значит, правильным является ответ 32.
|
Задание 27
|
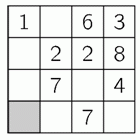
Аня хочет вписать числа во все клетки квадрата 4 × 4 так, чтобы суммы чисел во всех строчках и всех столбцах были одинаковыми. Несколько чисел она уже вписала, как показано на рисунке. Какое число она должна будет вписать в серую клетку?
A) 5 Б) 6 В) 7 Г) 8 Д) 9
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 64.25 + 5 = 69.25
|
Пусть число во второй клетке первой строчки равно x (см. рис.1).

Тогда сумма чисел в первой строчке равна
1 + x + 6 + 3 = x + 10.
Значит, согласно условию, сумма чисел во всех строчках и столбцах также равна x + 10. Поэтому число в нижней клетке второго столбца равно
(x + 10) – x – 2 – 7 = 1.
Аналогично, если число в нижней клетке правого столбца равно y, то сумма чисел в правом столбце равна
3 + 8 + 4 + y = y + 15.
Тогда и сумма чисел в нижней строчке тоже равна y + 15. Поэтому число в серой клетке должно быть равно
(y + 15) – 1 – 7 – y = 7.
Хотя правильный ответ уже найден, отметим, что если продолжить заполнение таблицы до конца, то получим единственно
возможный результат, приведённый на рис.2.
Задание 28
|
Алиса, Белла и Виктория устроили соревнование по армрестлингу. В каждом поединке боролись две девушки, в то время как третья отдыхала. После каждого поединка победительница продолжала борьбу с той девушкой, которая отдыхала. Известно, что Алиса участвовала в 10 поединках, Белла – в 15, а Виктория – в 17. Кто проиграл во втором поединке?
A) Алиса
Б) Белла
В) Виктория
Г) Алиса или Белла
Д) Алиса или Виктория
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 69.25
Найдём число всех поединков. По условию, Алиса участвовала в 10 поединках, Белла – в 15, а Виктория – в 17. При этом в каждом поединке участвовали две девушки. Поэтому общее число поединков равно
(10 + 15 + 17) : 2 = 21.
Заметим также, что если Алиса в каком-то поединке не участвовала, то она обязательно участвовала в следующем после него поединке (с той девушкой, которая перед этим победила). Другими словами, по крайней мере, в одном из двух подряд идущих поединков Алиса обязательно участвовала. Но Алиса провела 10 поединков из 21 и в 11 поединках не участвовала. Это означает, что во всех нечётных поединках Алиса не участвовала, а во всех
чётных участвовала, причём каждый раз проигрывала. В частности, во втором поединке она участвовала и проиграла. Поэтому правильным является ответ Алиса.
|
Задание 29
|
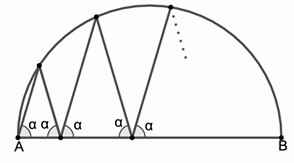
Ломаная вписана в полукруг. Она начинается в точке A диаметра AB и заканчивается в точке B (см. рис.). Внутри дуги полукруга ломаная имеет 4 вершины. Все углы между отрезками ломаной и диаметром AB равны α. Чему равен угол α?
A) 60° Б) 72° В) 75° Г) 80° Д) другой ответ
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 69.25
Отразим симметрично данную ломаную вместе с полуокружностью относительно её диаметра AB (см. рис.).

Легко видеть, что данная ломаная ACLDOENFB симметрична относительно диаметра, перпендикулярного диаметру AB (штриховая линия). В частности, точка O является центром
полученной окружности и, значит, угол ∠AOD = α является центральным углом данной окружности. Тогда угловая величина дуги ACD равна α.
Далее, в силу симметричности ∠ALK = ∠DLO = α. Поэтому точки K, L и D лежат на одной прямой. Тогда

Подсчитывая сумму углов в треугольнике AKL, получаем
2α + β = 180°, или
2,5α = 180°, откуда α = 72°.
По-другому найти правильный ответ можно было, например, так. Снова отразим данную ломаную вместе с полуокружностью относительно её диаметра AB. Снова заметим, что вершины ломаной, расположенные на диаметре AB, лежат на образовавшихся хордах: точка L лежит на хордах KD и CM, O – на хордах ME и DP, N – на хордах ER и FP. Кроме того, эти хорды параллельны:
AC || KD || ME || PF || RB и
AK || CM || DP || ER || FB.
Дуги  в силу симметричности. Кроме того, поскольку дуги между параллельными хордами равны, имеем:
в силу симметричности. Кроме того, поскольку дуги между параллельными хордами равны, имеем:

и

Поэтому

Так как этих пять равных дуг образуют полуокружность, то

и тогда

|
Задание 30
|
Восемь последовательных трёхзначных натуральных чисел имеют следующее свойство: каждое из них делится на его последнюю цифру. Какова сумма цифр наименьшего из этих восьми целых чисел?
A) 10 Б) 11 В) 12 Г) 13 Д) 14
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 69.25
Последняя цифра любого набора из таких восьми чисел не может быть равна 0, поскольку на 0 деление невозможно. Таким образом, набор из 8 последовательных чисел должен иметь в качестве последних цифр либо 1, 2, 3, 4, 5, 6, 7, 8, либо 2, 3, 4, 5, 6, 7, 8, 9.
В первом случае данные восемь последовательных чисел делятся на 1, 2, 3, 4, 5, 6, 7, 8 соответственно. Пусть N – наименьшее из этих чисел. Тогда N + 1 делится на 2, N + 2 делится на 3, N + 3 делится на 4, …, N + 7 делится на 8. Отсюда следует, что
N – 1 = (N + 1) – 2 делится на 2,
N – 1 = (N + 2) – 3 делится на 3,
N – 1 = (N + 3) – 4 делится на 4, …,
N – 1 = (N + 7) – 8 делится на 8.
Видим, что число N – 1 делится на 2, 3, 4, 5, 6, 7, 8, а значит, делится на
НОК(2, 3, 4, 5, 6, 7, 8) = 3 · 5 · 7 · 8 = 840.
И поскольку N – трёхзначное число, то единственное значение N равно
840 + 1 = 841.
Во втором случае, аналогично, наименьшее из искомой восьмёрки чисел, число N, таково, что N – 1 делится на 3, 4, 5, 6, 7, 8, 9 и, значит, делится на
НОК(3, 4, 5, 6, 7, 8, 9) = 9 · 5 · 7 · 8 = 2520.
Видим, что в этом случае N не может быть трёхзначным. Таким образом, наименьшим в данной восьмёрке чисел является число 841. Сумма его цифр равна
8 + 4 + 1 = 13.
|
























 ,
, .
.








 в силу симметричности. Кроме того, поскольку дуги между параллельными хордами равны, имеем:
в силу симметричности. Кроме того, поскольку дуги между параллельными хордами равны, имеем:




