Задание 1
|

Какой из следующих блоков можно сложить из данных шести кирпичей?

|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 30
По условию, блок должен состоять из 2 белых и 4 серых кирпичей. Однако, во всех вариантах ответа, кроме Г, использовано 3 белых и 3 серых кирпича. Поэтому блоки в этих вариантах ответа построить из данного набора кирпичей нельзя. А блок в
ответе Г построить можно, что непосредственно легко видеть.
|
Задание 2
|

Сколько пар детей на рисунке держат друг друга за левую руку?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 30 - 0.75 = 29.25
|
У того из детей, кто на рисунке стоит к нам спиной, левая рука находится слева. А у того, кто стоит лицом, левая рука на рисунке находится справа. Поэтому держит друг друга левой рукой только одна пара, отмеченная на рисунке.

Задание 3
|
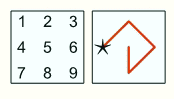
В квадрате на первом рисунке записаны цифры от 1 до 9. Будем строить число, начиная с цифры, указанной звездочкой, и последовательно записывая цифры, расположенные по ходу некоторой линии. Например, линия на втором рисунке задаёт число 42685. Какая из следующих линий задаёт наибольшее число?

|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 29.25

Все зашифрованные в вариантах ответа числа – пятизначные. Поэтому достаточно рассмотреть ответы Б и Д, числа в которых начинаются с наибольшей цифры – цифры 9. Но в ответе Б следующие две цифры 85, а в ответе Д – 86. Поэтому наибольшим из зашифрованных чисел является число в ответе Д.
Хотя правильный ответ уже найден, приведём полные значения всех зашифрованных чисел: А) 15786, Б) 98542, В) 26847, Г) 65742, Д) 98651.
|
Задание 4
|
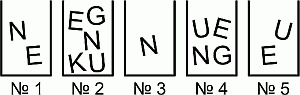
Софья хочет составить слово KENGU из букв, находящихся в коробках. Она может взять только одну букву из каждой коробки. Какую букву Софья должна взять из коробки №4?
A) K Б) E В) N Г) G Д) U
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 29.25
В слове KENGU пять разных букв и коробок тоже пять. Поэтому из каждой коробки Софья должна взять ровно одну букву. Из коробки №3 она может взять только букву N (см. рис.). Тогда из коробки №1 она может взять только букву E и, далее, из коробки №5 – только букву U. В результате из коробки №4 она должна
взять G.
По-другому этот ответ можно получить так. Заметим, что буква K имеется только в коробке №2. Поэтому из этой коробки нужно взять именно K. А буква G, помимо коробки №2, из которой нельзя взять вторую букву, имеется только в коробке №4. Следовательно, из коробки №4 можно взять только G.
|
Задание 5
|

Если правильно сложить 5 плиток пазла, получится прямоугольник с примером на сложение. Чему равен результат вычислений в этом примере?
A) 22 Б) 32 В) 41 Г) 122 Д) 203
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 29.25
Ясно, что пазл с цифрой 1 должен быть самым левым, а с цифрой 0 – самым правым. Остальные три пазла располагаются между ними. Заметим при этом, что два пазла с цифрами 2 не могут быть соседними. Поэтому из данных пазлов можно сложить только такой прямоугольник, который приведён на рисунке.

Результат вычислений в получившемся примере равен 12 + 20 = 32.
|
Задание 6
|
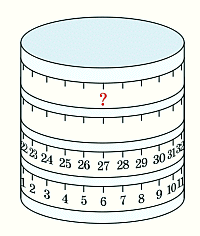
На цилиндр намотали мерную ленту, как показано на рисунке. Какое число стоит на месте, обозначенном знаком вопроса?
A) 53 Б) 60 В) 69 Г) 77 Д) 81
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 29.25 + 3 = 32.25
|
На рисунке в условии задачи видно, что после одного оборота мерной ленты числа по вертикали увеличиваются на 21. Так, например, над числом 6 находится число 27 = 6 + 21. Тогда над числом 27 должно быть число 27 + 21 = 48, а над числом 48 (т. е. на месте, обозначенном знаком вопроса) – число 48 + 21 = 69.
Задание 7
|
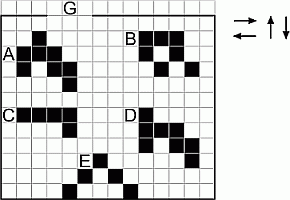
Пять фигур на клетчатой поверхности могут перемещаться только в направлениях, указанных стрелками. Какая из них может выйти через ворота G?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 32.25 - 0.75 = 31.5
|
Из условия следует, что фигуры нельзя поворачивать. Поэтому фигура не пройдёт через ворота ширины 3, если её ширина по какой-то из горизонталей больше 3. То есть не проходит, если в какой-то строчке между крайними чёрными кубиками фигуры находится более одного кубика (чёрного или белого). Такими фигурами являются A, C, D и E. На рисунке у них отмечены крестиками крайние клетки горизонталей, которые не проходят в ворота. У фигуры B по всем горизонталям ширина равна 3, и эта фигура проходит через ворота.

Задание 8
|
Карина собирается покрасить стены в своей комнате в зелёный цвет. Зелёная краска слишком тёмная, поэтому она решила смешать её с белой краской. Какая из следующих смесей даст самый светлый зелёный цвет?
A) 1 часть зелёной + 3 части белой
Б) 2 части зелёной + 6 частей белой
В) 3 части зелёной + 9 частей белой
Г) 4 части зелёной + 12 частей белой
Д) все смеси дают один и тот же цвет
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 31.5 + 3 = 34.5
|
Во всех первых четырёх вариантах ответа на 1 часть зелёной краски приходится 3 части белой. Поэтому правильным является ответ Д все смеси дают один и тот же цвет.
Задание 9
|
У Марии был лист бумаги. Она сложила его ровно пополам. Потом снова сложила ровно пополам. В результате получился треугольник:  .
.
Какой из следующих могла быть исходная форма листа?
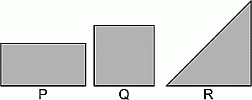
A) только P
Б) только Q
В) только R
Г) только P и Q
Д) любая из указанных
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 34.5 + 3 = 37.5
|
На следующих рисунках показано, что каждый из трёх данных листов бумаги можно сложить так, что получится приведённый в условии задачи треугольник. Поэтому форма листа могла быть любая из указанных.

Задание 10
|
Внутри квадрата нарисованы отрезки. Концами отрезков, помимо одной вершины, являются середины других отрезков или сторон квадрата. В каком из следующих ответов окрашена восьмая часть площади данного квадрата?

|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 37.5

В варианте А) данный квадрат разбит штриховыми линиями на 4 равных квадрата. В свою очередь, один из них также разбит на 4 равных квадрата. Окрашенная клетка является четвёртой частью одного из последних. Поэтому её площадь составляет 1/4 ⋅ 1/4 ⋅ 1/4 = 1/64 от площади данного квадрата.

В варианте Б) данный квадрат разбит штриховыми линиями также на 4 равных квадрата. Один из них
разбит вертикальной штриховой линией на два равных прямоугольника. Окрашенный треугольник по площади составляет половину от одного такого прямоугольника. Поэтому окрашенная часть составляет 1/2 ⋅ 1/2 ⋅ 1/4 = 1/16 от площади данного квадрата.

В варианте В) данный квадрат разбит вертикальной штриховой линией на два равных прямоугольника. Окрашенный треугольник по площади составляет половину от одного такого прямоугольника. Поэтому окрашенная часть составляет 1/2 ⋅ 1/2 = 1/4 от площади данного квадрата.

В варианте Г) данный квадрат разбит штриховыми линиями на 4 равных квадрата. Окрашенный треугольник составляет по площади половину от одной из таких четвертей. Поэтому окрашенная часть составляет 1/2 ⋅ 1/4 = 1/8 от площади данного квадрата.

Наконец, в варианте Д), легко видеть, площадь заштрихованной части составляет 1/4 от площади данного квадрата.
Видим, что правильным является ответ Г.
|
Задание 11
|
На полоске бумаги было записано число 5021972970. Юля разрезала полоску на три части так, что получилось три числа. Какую наименьшую сумму могли иметь эти три числа?
A) 3244 Б) 3444 В) 5172 Г) 5217 Д) 5444
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 37.5
Данное число 5021972970 состоит из 10 цифр. Если его разбить на 3 части так, как сказано в условии задачи, то по крайней мере одно из слагаемых будет состоять не менее чем из
4-х цифр. Поэтому любая сумма полученных при разбиении чисел – не менее чем 4-значное число. Сумма будет тем меньше, чем меньше старшие цифры самых больших по количеству цифр слагаемых. Поэтому наименьшее 4-значное число, которым может оказаться одно из слагаемых, – это число 1972 (начинается с цифры 1). Соответствующее разбиение даёт сумму
502 + 1972 + 970 = 3444.
(Даже если допустить, что число может начинаться с цифры 0, то всё равно мы получаем сумму, не меньшую
5 + 02197 + 2970 > 5000 > 3444.)
Покажем, что сумма 3444 – наименьшая. Действительно, если хоть одно из слагаемых – 5-значное число, то сумма будет больше полученной. Если первое слагаемое является 4-значным, то сумма больше 5021 и, тем самым, больше 3444. Если второе и третье слагаемые – 4-значные числа, то соответствующая сумма
50 + 2197 + 2970 > 5000 > 3444.
Если только третье слагаемое 4-значное, то соответствующая сумма равна
502 + 197 + 2970 = 3669 > 3444.
Итак, наименьшая сумма равна 3444.
|
Задание 12
|

A, B и C на карте – автобусные станции. Круговой маршрут, соединяющий станцию А с зоопарком и портом, составляет 10 км. Круговой маршрут, соединяющий станцию B с парком и зоопарком, составляет 12 км. Круговой маршрут, соединяющий станцию C с портом и парком, составляет 13 км. А круговой маршрут, соединяющий зоопарк, парк и порт, имеет протяженность 15 км. Какова длина кругового маршрута, соединяющего все станции? (Каждый круговой маршрут проходит только по указанным в нём станциям и не проходит ни через какую станцию или дорогу дважды.)
A) 18 км Б) 20 км В) 25 км Г) 35 км Д) 50 км
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 37.5
Суммарная длина трёх круговых маршрутов, проходящих через станции A, B и C, равна 10 + 12 + 13 = 35 км. Заметим, что эти три маршрута образованы в точности всеми дорогами на схеме, взятыми по одному разу. Если удалить из этих трёх маршрутов дороги, расположенные внутри схемы, то как раз останутся дороги, образующие круговой маршрут между станциями. А так как внутренние дороги образуют маршрут длиной 15 км, то маршрут между станциями имеет длину 35 – 15 = 20 км.
|
Задание 13
|

Роза хочет вставить отсутствующую плитку в центр квадрата так, чтобы можно было по линиям пройти от левой стрелки до правой. Какая из следующих плиток для этого НЕ подходит?

|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 37.5 + 4 = 41.5
|
Выделим линию, идущую от левой стрелки в направлении этой стрелки, и линию, идущую от правой стрелки в противоположном к этой стрелке направлении (см. рис.).

Видим, что они обрываются в двух чёрных точках на границе отсутствующей плитки. Поэтому, чтобы получить нужный путь, необходимо, чтобы эти две точки соединялись линией непосредственно на плитке, которую следует положить в центр квадрата, или соединялись через две правые точки на границе отсутствующей плитки. (Линии, идущие вверх и вниз от границы отсутствующей плитки, не имеют общих точек с выделенными линиями и ведут за границы квадрата.) Легко видеть, что таким свойством не обладает только плитка Г.
Задание 14
|
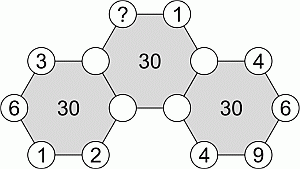
В вершины трёх шестиугольников вписаны числа. Некоторые числа указаны на рисунке, а числа в пустых кружочках скрыты. Сумма шести чисел в вершинах каждого шестиугольника равна 30. Какое число находится в вершине, отмеченной знаком вопроса?
A) 3 Б) 4 В) 5 Г) 6 Д) 7
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 41.5 - 1 = 40.5
|

Сумма четырёх указанных на рисунке чисел в вершинах левого шестиугольника равна
3 + 6 + 1 + 2 = 12.
Тогда сумма двух неизвестных чисел
a + b = 30 – 12 = 18.
Аналогично, сумма известных чисел в вершинах правого шестиугольника равна
4 + 9 + 6 + 4 = 23.
Тогда сумма двух неизвестных чисел
c + d = 30 – 23 = 7.
Тогда в среднем шестиугольнике сумма чисел в пяти вершинах
a + b + c + d + 1 = 18 + 7 + 1= 26.
Следовательно, шестое (искомое) число
x = 30 – 26 = 4.
Задание 15
|
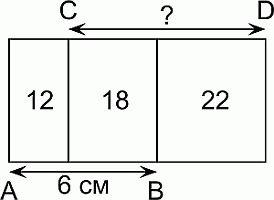
На рисунке изображены три прямоугольника, имеющие общую высоту. Чему равна длина отрезка CD, если известно, что AB = 6 см?
A) 7 см Б) 7,5 см В) 8 см Г) 8,2 см Д) 8,5 см
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 40.5 - 1 = 39.5
|

Пусть h – высота данных прямоугольников. Тогда
6h = AB • h = 12 + 18 = 30,
откуда h = 30 : 6 = 5.
Далее, CD • 5 = CD • h = 18 + 22 = 40,
откуда находим CD = 40 : 5 = 8.
Задание 16
|

Пирамида на рисунке состоит из 10 шаров одинакового радиуса. На каждом шаре написана одна из букв A, B, C, D или E. Каждой буквой помечено по 2 шара. На рисунке также показаны три вида пирамиды сбоку. Какой буквой помечен шар со знаком вопроса?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: А
|
Ответ участника: Б
|
Промежуточный результат: 39.5 - 1 = 38.5
|
Заметим, что верхний шар пирамиды виден на всех боковых гранях. Им является шар А. Согласно условию, среди шаров есть ещё один шар с буквой А. Но других букв А среди указанных на рисунке нет. В то же время каждый из десяти шаров можно видеть хотя бы на одной боковой грани. Следовательно, на шаре, отмеченном знаком вопроса, должна быть буква А.
Задание 17
|
У Ромы было четыре белых жетона, а у Вани – четыре серых. Мальчики играли в игру, в которой они по очереди выкладывали по одному из своих жетонов в какую-то из двух стопок. Первым ходил Рома. Какая из следующих пар стопок у них не могла получиться?

|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.5
Заметим, что последний жетон, который положит Ваня, будет верхним в одной из стопок. То же самое можно сказать о последнем жетоне Ромы. Поэтому при любом ходе игры в одной стопке верхний жетон должен быть серым (последний ход Вани), а в другой – белым (последний ход Ромы). Следовательно, стопки в варианте ответа Д не могли получиться. Поскольку, по правилам конкурса, ровно один из ответов правильный, им является ответ Д.
Хотя правильный ответ уже найден, покажем, что стопки в других вариантах ответа получиться могли. Соответствующие примеры приведены ниже, числа на жетонах указывают номера ходов.

|
Задание 18
|
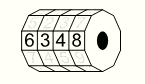
У моего младшего брата есть 4-значный велосипедный замок с цифрами от 0 до 9, записанными по возрастанию на каждом кольце. Он начал с правильной комбинации (открывающей замок) и на всех кольцах сделал одинаковые повороты в одном и том же направлении. В результате он получил комбинацию 6348. Какая из следующих комбинаций не может быть правильной?

|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 38.5 + 4 = 42.5
|
Комбинация В) 4906 начинается с цифры 4, которая на 2 меньше первой цифры полученной комбинации 6348. Если в комбинации 6348 уменьшить на 2 все цифры, получится комбинация 4126, которая может быть единственной начинающейся с цифры 4 правильной комбинацией. Следовательно, комбинация В) 4906 не может быть правильной.
Легко убедиться, что комбинации в других вариантах ответа могли быть правильным. Вообще, последовательно уменьшая в данной комбинации 6348 все цифры на 1 (при уменьшении цифры 0 происходит переход к цифре 9), можно выписать все комбинации, которые могут быть правильными. Они приведены ниже.

Задание 19
|
В коробке находилось 20 яблок и 20 груш. Коля наугад взял 20 фруктов из коробки, а остальные взял Лёша. Какое из следующих утверждений заведомо верно?
A) Коля взял, по крайней мере, одну грушу.
Б) Коля взял столько же яблок, сколько и груш.
В) Коле досталось столько же яблок, сколько и Лёше.
Г) Коля взял столько же груш, сколько яблок взял Лёша.
Д) Коле досталось столько же груш, сколько и Лёше.
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 42.5 - 1 = 41.5
|
Коля взял 20 фруктов: яблок и груш. Если все его груши заменить всеми яблоками, которые достались Лёше, то у Коли снова будет 20 фруктов, поскольку всего в коробке было 20 яблок. Следовательно, у Коли столько груш, сколько яблок досталось Лёше. Видим, что утверждение Г верное.
Остальные ответы не являются заведомо верными, поскольку Коля мог взять любое количество груш от 0 до 20. В частности, он мог не взять ни одной груши, что противоречит А), и мог не взять 10 груш, что противоречит утверждениям Б), В) и Д).
По-другому найти правильный ответ можно так. Пусть Коля взял x груш. Тогда он взял 20 – x яблок. Остальные 20 – (20 – х) = х яблок достались Лёше. Видим, что у Коли столько же груш, сколько у Лёши яблок.
Задание 20
|
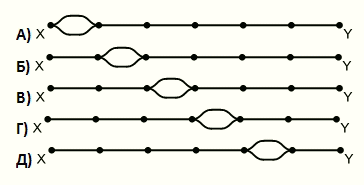
Станции X и Y соединяет единственный железнодорожный путь. Железнодорожная компания хочет одновременно отправлять один поезд из X в Y и один из Y в X. Поезда движутся с постоянными скоростями. Время на дорогу от X до Y составляет 180 минут, а от Y до X – 60 минут. На каком из участков следует построить разъезд, чтобы избежать столкновения?
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 41.5
Дорога между X и Y разбита на 6 равных участков. По условию, время поезда на дорогу от X до Y составляет 180 минут, а от Y до X – 60 минут, что в 180 : 60 = 3 раза меньше. Это значит, что поезд от X до Y движется в 3 раза медленнее, чем встречный поезд. И пока он преодолеет 1 участок, встречный поезд преодолеет 3 участка. После этого их будут разделять 2 участка. Тогда, если поезд от X до Y преодолеет половину следующего участка, встречный
поезд преодолеет 3 такие же половины. В результате вместе они покроют последние 2 участка. Видим, что поезда встретятся в середине второго слева участка. Следовательно, именно на этом участке следует построить разъезд. Таким образом, правильным является ответ Б.
|
Задание 21
|
Аня, Боря, Валя, Гена и Дима сидят за круглым столом. Аня сидит не рядом с Борей, Гена рядом с Димой, а Боря – не рядом с Геной. Кто сидит рядом с Валей?
A) Аня и Боря
Б) Боря и Гена
В) Гена и Дима
Г) Дима и Аня
Д) невозможно определить
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 41.5 - 1.25 = 40.25
|
Решение 1.

Согласно условию, Б (Боря) сидит не рядом с А (Аней) и не рядом с Г (Геной). При этом за столом сидят 5 человек. Поэтому пара А и Г сидит
напротив Б, как показано слева на рис.1. Ещё два места отмечены знаком «?». Их занимают В (Валя) и Д (Дима). По условию, Г и Д сидят рядом. Поэтому рассадка всех пятерых (с точностью до симметрии) такая, как справа на рис.1. Видим, что рядом с В сидят А и Б. Таким образом, правильным является ответ А.
Решение 2.

Г и Д сидят рядом, как показано слева на рис.2. В не может быть рядом с Г, потому что тогда два оставшихся соседних места были бы для A и Б. Но, по условию, А и Б не сидят рядом. Точно так же В не может быть рядом с Д. Поэтому В сидит напротив пары Г и Д, как показано справа на рис.2. Тогда рядом с В на двух оставшихся местах (в каком-то порядке) сидят A и B.
Заметим, что в этом решении нам не понадобилось условие, что Б и Г не сидят рядом. Приведём ещё одно решение, которое не использует это условие.
Решение 3.

По условию, A и B не сидят рядом друг с другом и всего за столом сидит 5 человек. Поэтому с одной стороны
между A и B сидит один человек (вверху
на рис. 3), а с другой – два (внизу на рис.
3). Но Г и Д, по условию, сидят рядом. Поэтому они в каком-то порядке занимают два соседних места внизу на рис.3, а В занимает одиночное место вверху на рис.3. Видим, что В сидит между А и Б.
Задание 22
|
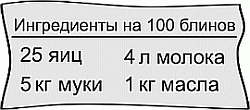
Маша получила у повара рецепт приготовления блинов. У неё есть 6 яиц, 400 г муки, 0,5 л молока и 200 г масла. Какое наибольшее количество блинов Маша сможет приготовить по этому рецепту?
A) 6 Б) 8 В) 10 Г) 12 Д) 15
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 40.25
Согласно рецепту, для приготовления одного блина нужно 0,25 яйца, 0,04 л молока, 0,05 кг муки и 0,01 кг масла. Тогда 6 яиц достаточно для приготовления 6 : 0,25 = 24 блинов; 400 г (т.е. 0,4 кг) муки – для 0,4 : 0,05 = 8 блинов; 0,5 л молока – для 0,5 : 0,04 = 12,5 блинов; 200 г (т.е. 0,2 кг) масла – для 0,2 : 0,01 = 20 блинов. Видим, что из имеющихся ингредиентов Маша в полном соответствии с рецептом может приготовить самое большее 8 блинов.
|
Задание 23
|

На рисунке показаны три шестерёнки. На каждой имеется по одному чёрному зубу. Как будут расположены чёрные зубья, если меньшая шестерёнка совершит полный оборот?

|
Правильный ответ: А
|
Ответ участника: Д
|
Промежуточный результат: 40.25 - 1.25 = 39
|
Меньшая шестерёнка имеет 10 зубьев. Поэтому если она совершит полный поворот, т.е. поворот на 10 зубьев, по ходу часовой стрелки, то нижняя шестерёнка тоже совершит поворот на 10 зубьев, но против хода часовой стрелки, а тогда правая – на 10 зубьев по ходу часовой стрелки. Отсчитаем на этих шестерёнках по 10 зубьев в соответствующих направлениях (см. рис.). 10-ые зубья на них будут после поворота чёрными. Следовательно, правильным является ответ А.

Задание 24
|
Яблоко и апельсин весят столько же, сколько груша и персик. Яблоко и груша весят меньше апельсина и персика, а груша и апельсин весят меньше яблока и персика. Какой из этих фруктов самый тяжелый?
A) яблоко
Б) апельсин
В) персик
Г) груша
Д) невозможно определить
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 39 + 5 = 44
|
Пусть яблоко весит Я (единиц веса), апельсин – А, груша – Г и персик – П. Тогда согласно условию задачи,
Я + А = Г + П, (1)
Я + Г < А + П, (2)
Г + А < Я + П. (3)
Сложив (1) и (2), получим
Я + А + Я + Г < Г + П +А + П,
откуда Я < П. А тогда, согласно (1), Г < А.
Аналогично, складывая (1) и (3), после упрощения получим А < П, и тогда, согласно (1), Г < Я.
Четыре полученных неравенства можно записать как два двойных неравенства:
Г < Я < П, (4)
Г < А < П. (5)
Видим, что самый большой вес (П) имеет персик.
Задание 25
|

Какое наименьшее количество клеток в квадрате на рисунке нужно ещё закрасить, чтобы полученный рисунок имел 4 оси симметрии?
A) 1 Б) 9 В) 12 Г) 13 Д) 21
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 44
Единственные четыре оси симметрии квадрата – это прямые, проходящие через середины противоположных сторон, и прямые, проходящие по диагоналям. Проведём эти прямые и будем последовательно отражать относительно них тройки закрашенных клеток. Результат показан на рисунке. Подсчёты показывают, что для получения требуемого рисунка нужно закрасить ещё не менее 21 клетки.

|
Задание 26
|
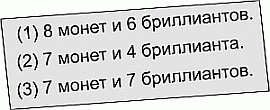
Трёх пиратов спросили, сколько монет и сколько бриллиантов имеет их друг Серая Борода. Каждый из троих ответил правдиво на один из вопросов, но солгал на другой. Их ответы приведены на рисунке. Сколько вместе монет и бриллиантов у Серой Бороды?
A) 11 Б) 12 В) 13 Г) 14 Д) 15
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 44 - 1.25 = 42.75
|
Если бы первое утверждение второго и третьего пиратов было ложным (они оба сказали «7 монет»), то, по условию задачи, их вторые утверждения были бы правдивыми. Но этого не может быть, потому что их вторые утверждения разные и, следовательно, не могут быть оба правдивыми. Следовательно, «7 монет» – правдивое утверждение. А тогда у первого пирата верным является второе высказывание: «6 бриллиантов». Таким образом, общее количество монет и бриллиантов у Серой Бороды равно 7 + 6 = 13.
Задание 27
|

На каждой из трёх полок находится по 64 децилитра яблочного сока. Он разлит в бутылки трёх разных размеров: большие, средние и маленькие. Сколько децилитров сока содержится в средней бутылке?
A) 3 Б) 6 В) 8 Г) 10 Д) 14
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 42.75
Пусть вместимость большой бутылки равна Б дл, средней – С дл, маленькой – М дл. Тогда, согласно условию задачи,
3Б + 4М = 64, (1)
2Б + 2С + 3М = 64, (2)
4С + 6М = 64. (3)
Из (3) следует
2С + 3М = 32. (4)
А тогда, согласно (2), получаем
2Б + 32 = 64, откуда Б = 16.
Далее, согласно (1), получаем
3 • 16 + 4М = 64, или 12 + М = 16, откуда М = 4.
Поэтому, согласно (4),
2С + 3 • 4 = 32, или С + 6 = 16, откуда С = 10. То есть объём средней бутылки 10 дл.
|
Задание 28
|
На каждой из шести граней куба со стороной 7 см нарисовали красным фломастером по две диагонали. Затем большой куб разрезали на кубики со стороной 1 см. На скольких маленьких кубиках будет нарисована хотя бы одна красная линия?
A) 54 Б) 62 В) 70 Г) 78 Д) 86
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 42.75

На рисунке видно, что по три красные линии будут на всех кубиках в вершинах данного куба. Число таких кубиков равно числу вершин куба и равно 8. Кроме того, красные линии будут на 9 внутренних кубиках каждой из шести граней куба (см. рис.). Число таких кубиков равно 9 · 6 = 54. Всего с красными линиями будет 8 + 54 = 62 кубика.
|
Задание 29
|
Группа состоит из 10 мифических существ – эльфов и троллей. Каждому из них выдали жетон с одним из чисел от 1 до 10, всем с разными числами. Затем у каждого из них спросили, какое число на его жетоне. Каждый назвал число от 1 до 10. Сумма названных чисел оказалась равна 36. При этом каждый тролль соврал, а каждый эльф сказал правду. Какое наименьшее количество троллей могло быть в этой группе?
A) 1 Б) 3 В) 4 Г) 5 Д) 7
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 42.75 - 1.25 = 41.5
|
Сумма чисел на всех десяти жетонах равна
1 + 2 + … + 10 = 55.
Это на 55 – 36 = 19 больше суммы названных чисел. Один тролль, солгав, может уменьшить число на жетоне не более
чем на 10 – 1 = 9 (при условии, что у него жетон с числом 10). Два тролля могут уменьшить эту сумму не более чем на 9 + 8 = 17 (при
условии, что у них жетоны с числами 10 и 9). Следовательно, троллей в группе не менее трёх. С другой стороны, если в группе ровно три тролля и если они, например, получили жетоны с числами 10, 9 и 8, а назвали соответственно числа 1, 1 и 6, то сумма всех названных чисел будет равна
1 + 2 + … + 7 + 6 + 1 + 1 = 36.
Таким образом, наименьшее
число троллей в группе равно 3.
Задание 30
|
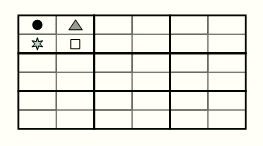
Прямоугольные карточки разделены на четыре равные ячейки, в которых нарисованы четыре разные фигурки. Из карточек можно сложить прямоугольник так, что соседние карточки будут соприкасаться друг с другом ячейками с одинаковыми фигурками. Одна из карточек этого прямоугольника показана на рисунке. Какой из следующих карточек заведомо НЕ может быть в таком прямоугольнике?

|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 41.5

На рисунках показано, что карточки А) – Г) (на рисунках они заштрихованы) в данном прямоугольнике быть могли. Здесь приведены только 4 карточки в левом верхнем углу прямоугольника. Что касается остальных карточек, то две карточки справа и две карточки ниже будем считать симметричными соседним карточкам на данных рисунках. Карточка в правом нижнем углу при этом может быть симметричной одновременно и левой, и верхней карточкам, как в примере Г) на рисунке выше. В результате все условия задачи будут соблюдены.
Таким образом, согласно правилам конкурса, верным является ответ Д. Покажем, тем не менее, что это действительно так. Обратим внимание, что в левом верхнем углу карточки Д) находится квадрат. Впишем квадраты в прямоугольнике из условия в те клетки, в которых они заведомо должны быть, и отметим крестиком те клетки, в которых их заведомо быть не может (см. рис. 1). Учитывая расположение квадрата на карточке Д), видим, что она могла бы располагаться только в центре прямоугольника. Поместим её туда и впишем в соответствующие клетки карточек слева и справа те фигурки, которые, по
условию, в них должны быть (см. рис. 2). Видим, что тогда в карточке слева должно быть две звёздочки. Противоречие.

|
















 .
.






































