Задание 1
|
Каждый год третий четверг марта называют Днём Кенгуру. Дата одного из следующих Дней Кенгуру указана неправильно. Какая именно?
A) 17 марта 2022 г.
Б) 16 марта 2023 г.
В) 14 марта 2024 г.
Г) 20 марта 2025 г.
Д) 19 марта 2026 г.
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 30 + 3 = 33
|
Так как неделя состоит из 7 дней, третий четверг не может приходиться на даты с 1 по 14. Поэтому дата 14 марта 2024 г. не может быть Днём кенгуру.
Задание 2
|
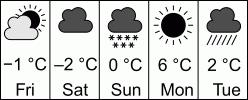
Женя каждый день просматривает приложение, которое показывает прогнозируемую погоду и максимальную температуру на ближайшие пять дней. В каком из следующих ответов приведён график максимальной температуры данного на рисунке прогноза?

|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 33 + 3 = 36
|
Согласно данным приложения, максимальная температура за данные пять дней была в четвёртый день. Поэтому все варианты ответа, кроме Б) и Г), заведомо неправильные. Но в варианте Г) первые три дня температура строго возрастала, что противоречит данным наблюдения. А вариант Б) полностью им соответствует, поэтому он и является правильным.
Задание 3
|
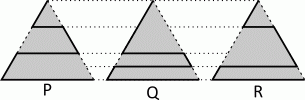
Парк имеет форму равностороннего треугольника. Кошка хочет пройти от верхней вершины до правой нижней вершины по одному из трёх путей, выделенных жирной линией. Длины путей обозначены буквами P, Q и R, как показано на рисунке. Какое из следующих соотношений является верным?
A) P < Q < R
Б) P < R < Q
В) P < Q = R
Г) P = R < Q
Д) P = Q = R
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 36 - 0.75 = 35.25
|
У всех трёх путей одна и та же нижняя часть (нижняя сторона треугольника). Кроме того, у них одинаковые суммы длин частей на боковых сторонах (вместе они составляют одну боковую сторону). Рассмотрим внутренние горизонтальные части. Обозначим их длины буквами a, b и c, как показано на рисунке.

Ясно, что a < b < c.
Поэтому a + b < a + c < b + c
и, следовательно, P < R < Q.
Задание 4
|
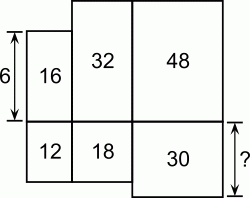
Шесть прямоугольников расположены так, как показано на рисунке. Левый верхний прямоугольник имеет высоту 6 см. Числа внутри прямоугольников указывают их площадь в см2. Какую высоту имеет правый нижний прямоугольник?
A) 4 см Б) 5 см В) 6 см Г) 7,5 см Д) 10 см
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 35.25 + 3 = 38.25
|

Мы имеем три пары прямоугольников с одинаковыми горизонтальными сторонами в каждой паре (см. рис.). Поэтому вертикальные стороны в каждой паре пропорциональны площадям данных прямоугольников. В левой паре вертикальная сторона нижнего прямоугольника равна 6 ⋅ 12/18 = 4 (см). А тогда в средней паре вертикальная сторона верхнего прямоугольника равна 4 ⋅ 32/16 = 8 (см). Наконец, в правой паре вертикальная сторона нижнего прямоугольника равна 8 ⋅ 30/48 = 5 (см).
Задание 5
|
Первый тайм гандбольного матча закончился со счётом 9 : 14, т. е., команда гостей опережала команду хозяев на 5 мячей. Но во втором тайме хозяева забили вдвое больше голов, чем их соперники, и в результате выиграли матч с перевесом в 1 мяч. С каким счётом закончился матч?
A) 20 : 19
Б) 21 : 20
В) 22 : 21
Г) 23 : 22
Д) 24 : 23
|
Правильный ответ: Б
|
Ответ участника: Б
|
Промежуточный результат: 38.25 + 3 = 41.25
|
Пусть x – количество голов, забитых гостями во втором тайме. Тогда всего в матче они забили 14 + x голов, а хозяева забили 9 + 2x голов. Согласно условию,
9 + 2x = (14 + x) +1, откуда x = 6.
Следовательно, хозяева в матче забили
9 + 2 · 6 = 21 гол, а гости 14 + 6 = 20 голов. В результате матч закончился со счётом 21 : 20.
Задание 6
|
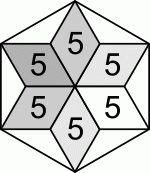
Шесть равных ромбов, каждый площадью 5 см2, образуют звезду. Концы звезды соединили отрезками, и в результате получился правильный шестиугольник, показанный на рисунке. Какую площадь он имеет?
A) 36 см2
Б) 40 см2
В) 45 см2
Г) 48 см2
Д) 60 см2
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 41.25 - 0.75 = 40.5
|
Звезду, составленную из шести ромбов, дополняют до шестиугольника шесть треугольников. Заметим, что, если два таких треугольника склеить по большей стороне, получится один такой же ромб, из которых состоит звезда. Поэтому площадь полученного шестиугольника равна площади звезды и ещё 3 ромбов, из которых она состоит, т.е. она равна площади 9 ромбов, а именно 9 · 5 = 45 см2.
Задание 7
|
В джаз-бэнде Джузеппе играет на саксофоне, Серджио – на трубе, а Элиана поёт. Все они одного возраста. В состав джаз-бэнда входят ещё трое участников, их возрасты: 19, 20 и 21 год. Средний возраст всех участников джаз-бэнда равен 21 году. Сколько лет Элиане?
A) 20 Б) 21 В) 22 Г) 23 Д) 24
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 40.5 - 0.75 = 39.75
|
Пусть x (лет) – возраст Джузеппе, Серджио и Элианы. Тогда, согласно условию,
(3x + 19 + 20 + 21)/6 = 21, или
3x + 60 = 126, откуда x = 22.
Задание 8
|
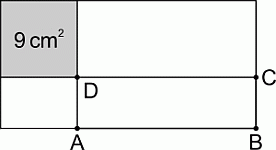
Прямоугольник с периметром 30 см разбит на 4 прямоугольника, как показано на рисунке. Один из них – квадрат площадью 9 см2. Чему равен периметр прямоугольника ABCD?
A) 14 см Б) 16 см В) 18 см Г) 21 см Д) 24 см
|
Правильный ответ: В
|
Ответ участника: А
|
Промежуточный результат: 39.75 - 0.75 = 39
|
Легко видеть, что сумма периметров данного квадрата и прямоугольника ABCD равна периметру всего прямоугольника. По условию, периметр всего прямоугольника равен 30 см. Квадрат площади 9 см2 имеет сторону 3 см, а его периметр равен 4 · 3 = 12 см. Поэтому периметр прямоугольника ABCD равен 30 – 12 = 18 см.

Немного по-другому ответ можно найти так. Определив, что сторона серого квадрата равна 3, обозначим стороны прямоугольника ABCD через a и b (см. рис.). Тогда стороны всего данного прямоугольника равны a + 3 и b + 3. Вычисляя его периметр, получаем уравнение
2(a + 3) + 2(b + 3) = 30, откуда
2a + 2b = 18. А это и есть периметр ABCD.
Задание 9
|
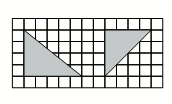
Алла нарисовала на клетчатой бумаге три треугольника. Ровно два из них имеют одинаковую площадь, ровно два из них равнобедренные, и ровно два – прямоугольные. На рисунке показаны два из этих треугольников. Каким может быть третий?

|
Правильный ответ: Г
|
Ответ участника: Д
|
Промежуточный результат: 39 - 0.75 = 38.25
|
Данные два треугольника – прямоугольные. У одного из них катеты 4 и 5, у другого 4 и 4. В частности, их площади равны 10 и 8, и один из них – равнобедренный. Поэтому, согласно условию, третий треугольник должен быть непрямоугольным, равнобедренным, площади 8 или 10. Равнобедренные непрямоугольные треугольники изображены только в ответах В и Г. В первом случае площадь равна 0,5 ⋅ (4 ⋅ 6) = 12 , а во втором 0,5 ⋅ (4 ⋅ 4) = 8. Видим, что правильным является ответ Г.
Задание 10
|
Кенгурёнок обнаружил любопытное число: если вычесть из него 1/10, то получится такой же результат, как и при умножении этого числа на 1/10. Какое число обнаружил кенгурёнок?
A) 1/100 Б) 1/11 В) 1/10 Г) 11/100 Д) 1/9
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
Обозначим любопытное число через x. Согласно условию,
x - 1/10 = x ⋅ 1/10, т.е.
x (1 - 1/10) = 1/10, откуда
x = 1/10 : 9/10 = 1/9.
Задание 11
|
У Тома было десять бенгальских огней одинакового размера. Он зажёг первый из них. Когда до его сгорания оставалась десятая часть, он зажёг второй. Когда до сгорания оставалась десятая часть второго огня, он зажёг третий огонь и т.д. Бенгальские огни горят с одинаковой скоростью по всей длине. Один бенгальский огонь сгорает за 2 минуты. За какое время сгорели все 10 огней?
A) 18 мин 20 сек
Б) 18 мин 12 сек
В) 18 мин
Г) 17 мин
Д) 16 мин 40 сек
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 37.5 - 1 = 36.5
|
Согласно условию, каждый следующий бенгальский огонь зажигался через 0,9 · 2 = 1,8 минуты после предыдущего. Поэтому десятый огонь был зажжён через 9 · 1,8 = 16,2 минуты после первого и горел ещё 2 минуты. Таким образом, все огни сгорели за 16,2 + 2 = 18,2 минуты, т.е. за 18 мин 12 сек.
Немного по-другому ответ можно найти так. Если бы каждый следующий бенгальский огонь зажигался ровно тогда, когда догорал предыдущий, то все 10 огней горели бы 10 · 2 = 20 минут. Но у нас имеется 9 опережений, каждое на 2 · 0,1 = 0,2 минуты. Поэтому последний огонь догорит на 9 · 0,2 = 1,8 минуты раньше. Следовательно, все огни будут гореть 20 – 1,8 = 18,2 минуты, т.е. 18 мин 12 сек.
Задание 12
|
Миша хочет подняться по лестнице на 8 ступенек. За один шаг он может подняться на 1 или 2 ступеньки. Но шестая ступенька сломана, поэтому он не может стать на неё. Сколько всего имеется различных способов, чтобы Миша мог дойти до 8-й ступеньки, став на неё?
A) 6 Б) 7 В) 8 Г) 9 Д) 10
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 36.5 - 1 = 35.5
|
Первое решение.
Поднимаясь вверх по лестнице, Миша может пропустить не более одной ступеньки, и на 6-ю ступеньку он не может стать. Поэтому он обязательно должен стать на 5-ю ступеньку. После этого продолжение пути однозначно: 5 → 7 → 8. Следовательно, количество различных путей равно количеству способов ступить на 5-ю ступеньку. Их нетрудно подсчитать непосредственно, если, например, принимать во внимание ступеньки до 5-й, которые можно пропустить. Есть только один способ не пропустить ни одной ступеньки, 4 способа пропустить ровно одну ступеньку (любую из первых 4-х) и 3 способа пропустить две не соседние ступеньки (либо 1 и 3, либо 1 и 4, либо 2 и 4). Больше половины (в нашем случае больше 2-х из 4-х) ступенек пропустить, соблюдая условие, нельзя. Всего имеем 1 + 4 + 3 = 8 способов.
Такой подсчёт было бы трудно реализовать, если бы нужно было найти число способов добраться до ступеньки с большим номером. Поэтому приведём другое решение, лишённое этого недостатка.
Второе решение.
Обозначим через fn число способов ступить на n-ю ступеньку с соблюдением условий задачи (при условии, что до неё сломанных ступенек нет). Легко видеть, что f1 = 1, f2 = 2. Далее, заметим, что справедлива формула:
fn+1 = fn–1 + fn для n ≥ 2.
Действительно, на (n + 1)-ю ступеньку можно ступить непосредственно только с одной из двух предыдущих ступенек: с n-й (поднявшись на 1 ступеньку) или с (n – 1)-й (поднявшись на 2 ступеньки). При этом число способов подняться на n-ю ступеньку равно fn, а на (n – 1)-ю – fn–1. Теперь, пользуясь формулой, легко находим:
f3 = 1 + 2 = 3,
f4 = 2 + 3 = 5,
f5 = 3 + 5 = 8,
f6 = 5 + 8 = 13,
f7 = 8 + 13 = 21, и т.д.
Полученная выше последовательность чисел fn называется последовательностью Фибоначчи. Вычисление чисел Фибоначчи и изучение их свойств играют важную роль при решении некоторых комбинаторных задач. См., например, задачу №29.
Задание 13
|
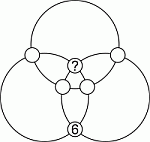
В кружочки на пересечениях трёх колец вписаны числа от 1 до 6. На рисунке указано положение числа 6. Суммы чисел, записанных во всех четырёх кружочках каждого кольца, одинаковы. Какое число находится в кружочке со знаком вопроса?
A) 1 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 35.5
По условию задачи, суммы чисел на всех трёх кольцах одинаковы. Сложим суммы чисел на всех трёх кольцах. Так как каждое из данных шести чисел находится на пересечениях ровно двух колец, получим
2 · (1 + 2 + 3 + 4 + 5 + 6) = 2 · 21 = 42.
По условию, суммы чисел на кольцах одинаковые. Поэтому сумма чисел на одном кольце равна 42 : 3 = 14. Рассмотрим два кольца, на которых есть число 6 и число, которое требуется найти. На каждом из них сумма трёх чисел, без числа 6, равна 8. Есть только два способа, как можно представить число 8 в виде трёх различных натуральных чисел от 1 до 5, а именно: 8 = 1 + 2 + 5 и 8 = 1 + 3 + 4. Заметим, что только число 1 является общим у этих двух сумм. Значит, только оно может быть искомым и, по правилам конкурса, верным является ответ 1.
Пример на рисунке показывает, что вписать числа так, как требуется в условии, можно.

Несколько по-другому закончить подсчёты можно было так. Только число 6 и искомое число (пусть оно равно x) не входят в сумму чисел на верхнем кольце. Как было установлено выше, сумма чисел на одном кольце равна 14, а сумма всех шести данных чисел равна 21. Поэтому 6 + x = 21 – 14 = 7, откуда x = 1.
|
Задание 14
|
Число 2021 при делении на 6, 7, 8 и 9 даёт один и тот же остаток 5. Сколько всего натуральных чисел, меньших 2021, тоже дают остаток 5 при делении на 6, 7, 8 и 9?
A) 4 Б) 3 В) 2 Г) 1 Д) ни одного
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 35.5 - 1 = 34.5
|
Пусть n – одно из искомых чисел. Из условия следует, что n – 5 делится на 6, 7, 8 и 9, т.е. делится на
НОK(6, 7, 8, 9) = НОK(2 · 3, 7, 23, 32) = 23 · 32 · 7 = 504.
Поэтому n = 504k + 5, где k – целое неотрицательное число. Чисел такого вида, меньших 2021, четыре:
504 · 0 + 5 = 5,
504 · 1 + 5 = 509,
504 · 2 + 5 = 1013,
504 · 3 + 5 = 1517.
Задание 15
|
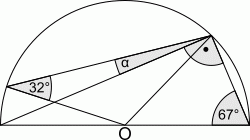
На рисунке показан полукруг с центром O и указаны величины двух углов. Какова величина угла α?
A) 9° Б) 11° В) 16° Г) 17,5° Д) 18°
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 34.5
Первое решение.

В треугольнике ACD угол ∠ACD = 90°, как вписанный, опирающийся на диаметр (см. рис.). Тогда
∠CAD = 90° – ∠CDA = 90° – 67° = 23°.
Далее, треугольник AOC – равнобедренный (OA = OC, как радиусы). Поэтому
∠ACO = ∠OAC = 23°.
Треугольник BOC – также равнобедренный (OB = OC, как радиусы). Поэтому
∠BCO = ∠OBC = 32°.
Тогда α = ∠ BCO – ∠ACO = 32° – 23° = 9°.
Второе решение.
В равнобедренных треугольниках COD и BOC (см. рис.) находим:
∠COD = 180° – 2 · 67° = 46° и
∠BOC = 180° – 2 · 32° = 116°.
Поэтому ∠AOB = 180° – 46° – 116° = 18°.
Угол ∠ACB вписан в окружность и опирается на дугу AB. Поэтому его величина равна половине величины центрального угла ∠AOB, т.е.
α = ∠ ACB = ∠AOB : 2 = 18° : 2 = 9°.
|
Задание 16
|
Имеется пять коробок, в каждой из которых лежат шары. Количества шаров в коробках соответственно равны: 9, 15, 17, 19 и 21. В каждой коробке либо все шары красные, либо все шары синие. Когда убрали одну из коробок, то в оставшихся четырёх коробках число красных шаров стало ровно в 3 раза больше числа синих. Сколько шаров было в убранной коробке?
A) 9 Б) 15 В) 17 Г) 19 Д) 21
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 34.5 - 1 = 33.5
|
Пусть после того, как одну коробку убрали, в четырёх коробках осталось n синих шаров и тогда, по условию, 3n красных. Тогда всего осталось n + 3n = 4n. Это означает, что число оставшихся шаров кратно 4. Всего во всех пяти коробках был
9 + 15 + 17 + 19 + 21 = 81 шар.
Если убрать одну из коробок, то число шаров в оставшихся коробках может равняться 81 – 9 = 72, 81 – 15 = 66, 81 – 17 = 64, 81 – 19 = 62 или 81 – 21 = 60 соответственно. Среди полученных чисел только три числа делятся на 4, а именно, числа 72, 64 и 60. Тогда число n синих шаров будет, соответственно, равно 72 : 4 = 18, 64 : 4 = 16, 60 : 4 = 15. Но из этих трёх чисел только число 15 является числом шаров одной из данных пяти коробок. Коробок (одной или нескольких) с 18 или 16 шарами нет. Следовательно, осталось 15 · 4 = 60 шаров, а в коробке, которую убрали, был 81 - 60 = 21 шар.
Задание 17
|
Пять автомобилей стартовали в следующем порядке:

Каждый раз, когда одна машина обгоняла другую, ей начислялось 1 очко. Машины финишировали в следующем порядке:

Каково наименьшее возможное общее количество всех начисленных очков?
A) 10 Б) 9 В) 8 Г) 7 Д) 6
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 33.5 + 4 = 37.5
|
Сравнивая порядок автомобилей на финише с тем, который был на старте, видим следующие результаты.

Автомобиль II опередил 3 автомобиля (III, IV и V – все те, которые на старте были у него впереди). Поэтому он получил по крайней мере 3 очка. Автомобиль IV опередил 1 автомобиль (а именно, V) и получил по крайней мере 1 очко. Автомобиль I опередил 2 автомобиля (III и V) и получил по
крайней мере 2 очка. Таким образом, число набранных очков не меньше 3 + 1 + 2 = 6. Пример, реализующий данное количество очков, получается, если сначала II последовательно обгоняет III, IV и V, затем IV обгоняет V, наконец, I
обгоняет III и V.
Задание 18
|

В каждой клетке квадрата 3 × 3 было записано число 0. За один ход можно увеличить на 1 числа во всех клетках какого-то из четырёх квадратов 2 × 2, содержащихся в квадрате 3 × 3 (например, в клетках серого квадрата на первом рисунке). После нескольких ходов получился квадрат, показанный на втором рисунке. Но некоторые числа в этом квадрате скрыты. Какое число может быть в клетке со знаком вопроса?
A) 14 Б) 15 В) 16 Г) 17 Д) 19
|
Правильный ответ: В
|
Ответ участника: Д
|
Промежуточный результат: 37.5 - 1 = 36.5
|
Пусть числа в угловых клетках таблицы увеличивались a, b, c и d раз. Тогда в результате должен получиться квадрат, изображённый на рисунке.

Заметим, что сумма чисел в трёх серых клетках равна числу в центральной клетке. Согласно данным на втором рисунке из условия задачи, 13 + 18 + d = 47, откуда d = 16.
Задание 19
|
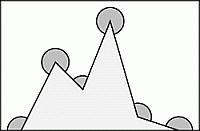
Чему равна сумма отмеченных на рисунке углов?
A) 360° Б) 900° В) 1080° Г) 1120° Д) 1440°
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 36.5 + 4 = 40.5
|
Первое решение.

Сумма всех отмеченных углов и углов заштрихованного шестиугольника равна
4 · 360° + 2 · 180° = 1800°.
В то же время, так как сумма внутренних углов n-угольника равна (n – 2) · 180°, сумма углов заштрихованного 6-угольника равна 4 · 180° = 720°. Поэтому сумма отмеченных углов равна 1800° – 720° = 1080°.
Второе решение.
Рассмотрим
10-угольник на рисунке.

Сумма всех его внутренних углов по формуле внутренних углов n-угольника, упомянутой в первом решении, равна
(10 – 2) · 180° = 1440°.
Четыре его угла – прямые, их сумма равна 4 · 90° = 360°. Тогда сумма остальных (т.е. отмеченных) углов равна 1440° – 360° = 1080°.
Задание 20
|
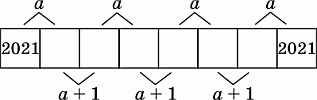
Полоска состоит из 8 клеток. Суммы чисел в парах соседних клеток равны a или a + 1, как показано на рисунке. Числа в крайних клетках равны 2021. Чему равно a?
A) 4041 Б) 4042 В) 4043 Г) 4044 Д) 4045
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 40.5
С одной стороны, сумма всех чисел в полоске равна 4a. С другой стороны, она равна
2 · 2021 + 3(a + 1).
Получаем уравнение
4a = 2 · 2021 + 3(a + 1), откуда a = 4045.
Другое, но более длинное, решение можно получить так. Начнём заполнять клетки полоски слева направо. В первой клетке стоит число 2021. В сумме со вторым оно даёт a. Поэтому число во второй клетке равно a – 2021. Это число в сумме с числом в третьей клетке даёт a + 1. Поэтому третье число равно
(a + 1) – (a – 2021) = 2022.
Далее, четвёртое число равно a – 2022, пятое равно
(a + 1) – (a – 2022) = 2023,
шестое – a – 2023, седьмое –
(a + 1) – (a – 2023) = 2024,
наконец, последнее число равно a – 2024. Но, по условию, последнее число равно 2021. Получаем уравнение
a – 2024 = 2021, откуда a = 4045.
Хотя для решения это не обязательно, легко вычислить значения всех чисел в данной полоске. Они приведены ниже.

|
Задание 21
|
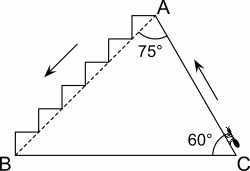
Муравей поднимается по наклонной тропинке CA и спускается по лестнице от A к B, как показано на рисунке. Чему равно отношение пути от С до A к пути от A до В?
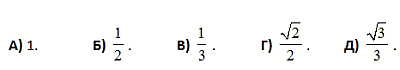
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 40.5

Проведём в треугольнике ABC высоту AH (см. рис.). Получим:
∠CAH = 90° – 60° = 30° и, значит,
∠BAH = 75° – 30° = 45°.
Тогда ∠DAH = 90° – 45° = 45°. Поэтому
BH = AH = AC · sin 60° =  , где a = AC.
, где a = AC.
Далее, проецируя вертикальные части ступенек на AH, а горизонтальные – на BH, видим, что путь муравья по ступенькам от A до B равен
BH + AH = 
Поэтому отношение путей равно

|
Задание 22
|
Числа a, b и c удовлетворяют равенствам a + b + c = 0 и abc = 78. Чему может быть равно выражение
(a + b) (b + c) (c + a)?
A) –156
Б) –39
В) 78
Г) 156
Д) ни одному из предыдущих
|
Правильный ответ: Д
|
Ответ участника: Г
|
Промежуточный результат: 40.5 - 1.25 = 39.25
|
Из уравнения a + b + c = 0 следует:
a + b = –c,
b + c = –a,
c + a = –b. Поэтому
(a + b) (b + c) (c + a) = (-c) (-a) (-b) = -abc = -78
Видим, что найденное значение не совпадает ни с одним значением в вариантах ответа A) – Г). Поэтому правильным является ответ Д.
Задание 23
|
Пусть N – наименьшее натуральное число, сумма цифр которого равна 2021. Чему равна сумма цифр числа N + 2021?
A) 10 Б) 12 В) 19 Г) 28 Д) 2021
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 39.25
Так как 9 – наибольшая из цифр и 2021 = 9 · 224 + 5, то данное число N состоит не менее чем из 225 цифр и наименьшее значение цифры в старшем разряде равно 5. Следовательно,
N = 5999...99 (5 и 224 цифры 9).
Тогда число N + 2021 = (N + 1) + 2020 = 6000…0000 + 2020 = 6000…02020.
Сумма цифр этого числа равна 6 + 2 + 2 = 10.
|
Задание 24
|
Трое мальчиков играют в игру «Слова», в которой они пишут по 10 слов. Каждый игрок получает 3 балла за каждое слово, которого нет у других игроков, а за каждое слово, которое встречается только у одного из двух других игроков, он получает 1 балл. За слова, которые встречаются у всех трёх игроков, баллов не начисляется. После игры мальчики подсчитали свои баллы, и оказалось, что у всех результаты разные. У Сени оказалось меньше всего – 19 баллов. Больше всего баллов оказалось у Димы. Сколько баллов набрал Дима?
A) 20 Б) 21 В) 23 Г) 24 Д) 25
|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 39.25 - 1.25 = 38
|
Так как Сеня получил 19 баллов, то 3-балльных слов у него не более шести, иначе только 3-балльные слова ему принесли бы не менее 7 · 3 = 21 балла. С другой стороны, 3-балльных слов у Сени не менее пяти, иначе всего он набрал бы не более
4 · 3 + 6 · 1 = 18 баллов.
Итак, 3-балльных слов у Сени 5 или 6. Рассмотрим эти два случая отдельно.
Пусть 3-бальных слов было 6. Они дают 6 · 3 = 18 баллов. Тогда, помимо этих шести слов, было одно 1-балльное слово и три 0-балльных слова. Тогда у каждого из игроков было по три 0-балльных слова. Поэтому максимальные количества баллов, которые могли получить Дима и третий игрок, – это
7 · 3 = 21 и 6 · 3 + 1 · 1 = 19.
Но последний результат – это количество баллов, набранных Сеней, а его количество баллов, по условию, наименьшее среди всех игроков и не совпадает с результатами других игроков. Противоречие.
Таким образом, у Сени было пять 3-балльных слов. Они дают 5 · 3 = 15 баллов. Значит, ещё 19 – 15 = 4 балла он получил за четыре 1-балльных слова. И из всех 10 слов за одно слово он получил 0 баллов. Тогда ровно по одному 0-балльному слову было и у двух других игроков. Кроме того, у них на двоих имеется 4 общих с Сеней 1-балльных слова.
Подсчитаем с учётом сделанных замечаний, сколько баллов мог набрать Дима и третий игрок. Если у Димы нет 1-балльных слов, то он набрал
9 · 3 + 0 · 1 + 1 · 0 = 27 баллов.
Тогда у третьего игрока по крайней мере четыре 1-балльных слова и, значит, он набрал не более
5 · 3 + 4 · 1 + 1 · 0 = 19 баллов.
Но 19 баллов набрал Сеня, и это – наименьший результат.
Если у Димы одно 1-балльное слово, то он набрал
8 · 3 + 1 · 1 + 1 · 0 = 25.
Тогда третий игрок мог набрать
6 · 3 + 3 · 1 + 1 · 0 = 21 балл.
В этом случае все условия задачи выполняются.
Если бы у Димы было два 1-балльных слова, то он набрал бы
7 · 3 + 2 · 1 + 1 · 0 = 23 балла.
Третий игрок, по условию, набрал меньше баллов, чем Дима. Поэтому у него
должно быть больше 1-балльных слов, чем у Димы. Заметим также, что сумма всех баллов, полученных игроками за 1-балльные слова, является чётной. Действительно, ведь за каждое 1-балльное слово по 1 баллу получают 2 игрока
(те, у которых это слово является общим). Тогда у третьего игрока не менее четырёх 1-балльных слов. В результате его сумма баллов не превосходит
5 · 3 + 4 · 1 + 1 · 0 = 19. Противоречие.
При увеличении количества 1-балльных слов у Димы их количество увеличивается и у третьего игрока, вследствие чего сумма его баллов становится строго меньше 19, что противоречит условию задачи. Таким образом, единственно возможное количество баллов у Димы равно 25.
Задание 25
|
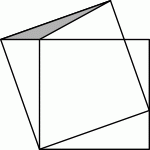
На рисунке площадь меньшего квадрата равна 16, а площадь серого треугольника равна 1. Чему равна площадь большего квадрата?
A) 17 Б) 18 В) 19 Г) 20 Д) 21
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 38

Опустим перпендикуляр LH из вершины L большего квадрата на сторону BC меньшего квадрата (см. рис.). В результате получим треугольник KLH, равный треугольнику AKB. Действительно, эти треугольники прямоугольные с равными гипотенузами (стороны большего квадрата) и равными острыми углами (их стороны перпендикулярны).
Пусть LH = KB = a. Тогда площадь SKLB = 0,5a2. С другой стороны, по условию, площадь этого треугольника равна 1. Поэтому 0,5a2 = 1, откуда a2 = 2. По условию, площадь меньшего квадрата равна 16 и, значит, его сторона равна 4. Тогда в треугольнике AKB по теореме Пифагора
KA2 = AB2 + KB2 = 42 + 2 = 18.
Поэтому площадь большего квадрата тоже равна 18.
|
Задание 26
|
Числа a и b являются квадратами целых чисел. Разность a – b является простым числом. Какое из следующих значений может принимать b?
A) 100 Б) 144 В) 256 Г) 900 Д) 10000
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 38
Пусть a = m2 и b = n2. Тогда, согласно условию,
a – b = (m – n) (m + n) = p – простое число.
Это возможно, только если (m – n) = 1 и (m + n) = p. Из этих двух равенств находим: p = 2n + 1. Подсчитаем для значений b, указанных в вариантах ответа, соответствующие значения p. Они приведены в следующей таблице.

Но здесь из найденных значений p только число 61 является простым. Поэтому правильным является ответ Г 900.
|
Задание 27
|
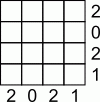
В таблице 4 × 4 некоторые клетки нужно окрасить в чёрный цвет. Числа, записанные справа от строчек и ниже столбцов, указывают, сколько чёрных клеток должно быть в соответствующей строчке или столбце. Сколько всего существует различных раскрасок, удовлетворяющих этим условиям?
A) 1 Б) 2 В) 3 Г) 5 Д) больше 5
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 38 + 5 = 43
|
По условию, во второй строчке и втором столбце не должно быть ни одной чёрной клетки. Поэтому данные строчку и столбец просто можно вычеркнуть и рассматривать таблицу 3 × 3 на рис.1. На ответ это никак не повлияет.

Теперь, если в левом верхнем квадрате 2 × 2 все клетки чёрные, то существует только одна удовлетворяющая условию раскраска (см. рис.2). Если в этом квадрате только одна клетка белая, то в каждом из четырёх возможных случаев раскраска клеток вне этого квадрата строится однозначно. Например, если белая клетка находится в первой строчке и втором столбце (рис.4), то за пределами данного квадрата 2 × 2 в этой же (т.е. в первой) строчке должна быть чёрная клетка (в третьем столбце) и в этом же втором столбце должна быть чёрная клетка (в третьей строчке). Все остальные клетки – белые. В результате имеется ещё 4 различные раскраски (рис. 3–6). Наконец, заметим, что всего (если, например, считать по строчкам) в таблице должно быть 2 + 2 + 1 = 5 чёрных клеток. Поэтому две или менее чёрных клеток в левом верхнем квадрате 2 × 2 быть не может. Иначе в третьей строчке и третьем столбце должно оказаться не менее трёх чёрных клеток, что невозможно. Видим, что всего существует 5 различных
удовлетворяющих условию раскрасок.
Задание 28
|
У скольких пятизначных натуральных чисел произведение цифр равно 1000?
A) 10 Б) 20 В) 30 Г) 40 Д) 60
|
Правильный ответ: Г
|
Ответ участника: нет ответа
|
Промежуточный результат: 43
Имеем каноническое разложение: 1000 = 23 · 53.
Поэтому, если произведение цифр пятизначного числа равно 1000, то три из этих цифр – это цифры 5, и ещё две цифры имеют произведение, равное 23 = 8. Есть два варианта: либо эти две цифры – это 2 и 4, либо это 1 и 8. В первом случае, чтобы получить из данных цифр пятизначное число достаточно выбрать два разряда из пяти для цифр 2 и 4 (остальные разряды займут цифры 5). Для цифры 2 можно выбрать любой из пяти разрядов (5 возможностей). При
любом выборе разряда для цифры 2, цифру 4 можно поместить в любой из 4-х оставшихся разрядов. Всего получаем 5 · 4 = 20 чисел. Ясно, что во втором случае (1 и 8, вместо 2 и 4) получим столько же чисел. Таким образом, всего нужное произведение цифр имеют 20 + 20 = 40 чисел.
|
Задание 29
|
У Кристины есть восемь монет, веса которых выражаются разными натуральными числами граммов. Как бы Кристина ни положила по две монеты на две чаши весов, всегда перевесит та чаша, на которой находится самая тяжёлая из четырёх монет на весах. Какой наименьший вес может быть у самой тяжёлой монеты?
A) 8 г Б) 12 г В) 34 г Г) 128 г Д) 256 г
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 43 + 5 = 48
|
Обозначим веса монет и упорядочим их по величине следующим образом:
a1 < a2 < a3 < a4 < a5 < a6 < a7 < a8.
Здесь все числа – натуральные, и требуется найти наименьшее значение a8. Из условия следует, что
ak+2 + a1 > ak+1 + ak для любого 2 ≤ k ≤ 6.
Заметим, что если a1 > 1, то все соотношения не изменятся, если каждое число (в том числе и a8) уменьшить на a1 – 1. Поэтому значение a8 будет наименьшим при a1 = 1. Тогда, a2 ≥ 2, a3 ≥ 3, и для любого 2 ≤ k ≤ 6 мы имеем:
ak+2 + 1 > ak+1 + ak, или
ak+2 ≥ ak+1 + ak.
Тогда a4 ≥ 3 + 2 = 5,
a5≥ 5 + 3 = 8,
a6 ≥ 8 + 5 = 13,
a7 ≥ 13 + 8 =21,
a8 ≥ 21 + 13 = 34.
Все условия сохранятся, если нестрогие неравенства выше заменить равенствами. Поэтому значение 34 для a8 достигается.
В заключение отметим, что полученная здесь последовательность 1, 2, 3, 5, 8, 13, 21, 34 и т.д. (с a1 = 1, a2 = 2 и условием ak+2 = ak+1 + ak для следующих значений) – это последовательность Фибоначчи, которая уже упоминалась в задаче №12.
Задание 30
|
2021 мяч выложены в ряд и пронумерованы числами от 1 до 2021. Каждый мяч окрашен в один из четырёх цветов: зелёный, красный, жёлтый или синий. Известно, что одновременно выполнены следующие три условия:
1) среди любых пяти подряд лежащих мячей есть ровно один красный, один жёлтый и один синий мяч;
2) после каждого красного мяча лежит жёлтый мяч;
3) мячи с номерами 2, 20 и 202 зелёные.
Какого цвета мяч номер 2021?
A) зелёный
Б) красный
В) жёлтый
Г) синий
Д) невозможно определить
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 48 - 1.25 = 46.75
|
Из условия следует, что среди любой пятёрки подряд лежащих мячей имеется ровно по одному красному, жёлтому и синему мячу и по два зелёных. Тогда цвета мячей повторяются с периодом 5. Действительно, если рассмотреть 6 подряд лежащих мячей, то мы имеем две такие пятёрки: первые 5 мячей и последние 5 мячей. 4 мяча в этих пятёрках общие. А расцветки всех пяти мячей в этих двух наборах одинаковые. Это возможно, только если цвет шестого мяча совпадает с цветом первого. Периодичность повторения цветов означает, что мячи, имеющие одинаковые остатки при делении на 5, имеют одинаковый цвет, и наоборот. По условию, 2-й шар зелёный. 20-й шар также зелёный, а значит, и 5-й шар зелёный. Поэтому первая пятёрка имеет вид: – З – – З (З означает зелёный; далее аналогично будем обозначать названия цветов мячей их заглавными буквами). По условию, красный и жёлтый мячи всегда расположены непосредственно друг за другом. Поэтому имеем уточнённый вид первой пятерки:
– З К Ж З. Наконец, окончательный вид: С З К Ж З. Видим, что первый мяч – синий. Значит, и 2021-й мяч – тоже синий.
Заметим, что данные в условии задачи о цвете 202-го мяча являются лишними, для решения они не понадобились.





























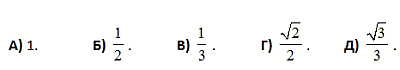

 , где a = AC.
, где a = AC.






