Задание 1
|
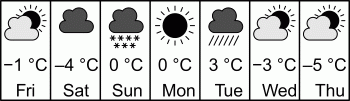
Павел просматривает приложение «Погода», которое показывает прогнозируемую погоду и максимальную температуру на ближайшие семь дней. В каком из следующих ответов приведён график максимальной температуры данного на рисунке прогноза?

|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 30 + 3 = 33
|
Непосредственно под таблицей данных о погоде построим график изменения температуры по дням недели (см. рис.).

Сравнивая его с вариантами ответа, видим, что правильным является ответ Д.
Задание 2
|
Сколько целых чисел находится в интервале
(20 – √21; 20 + √21)?
A) 9 Б) 10 В) 11 Г) 12 Д) 13
|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 33 + 3 = 36
|
Так как 4 < √21 < 5 , на интервале (−√21; √21)
находится 9 целых чисел (от –4 до 4 включительно). Если увеличить все числа на интервале (−√21; √21) на 20, получим интервал (20 − √21; 20 + √21). Целых чисел
на нём столько же, т.е. 9.
Задание 3
|
Куб с ребром 1 разрезали на два одинаковых параллелепипеда. Чему равна площадь поверхности одного такого параллелепипеда?
A) 1,5 Б) 2 В) 3 Г) 4 Д) 5
|
Правильный ответ: Г
|
Ответ участника: А
|
Промежуточный результат: 36 - 0.75 = 35.25
|

Все грани исходного куба имеют площадь 1. Пусть разрез проходит в горизонтальной плоскости (см. рис.). Тогда он разбивает боковые грани на равные прямоугольники площади 0,5. В результате площадь поверхности одного из полученных параллелепипедов равна
2 · 1 + 4 · 0,5 = 4.
Задание 4
|
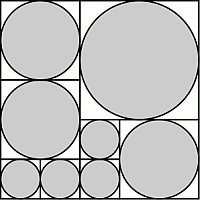
Большой квадрат разбит на меньшие квадраты так, как показано на рисунке. В каждый из этих квадратов вписали серый круг. Какая часть площади большого квадрата закрашена серым цветом?
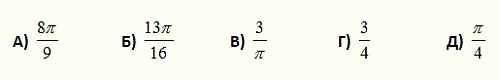
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 35.25
Пусть a – сторона квадрата.
Тогда его площадь равна a2, а площадь вписанного круга равна π/4 · a2. Видим,
что отношение этих площадей равно π/4 независимо от размера квадрата. Поэтому для любого количества квадратов любых размеров отношение суммы площадей вписанных в них кругов к сумме площадей этих квадратов также равно π/4. В нашем случае сумма площадей отдельных квадратов равна площади большого квадрата, который они образуют. Серая часть – совокупность вписанных в квадраты кругов. Поэтому закрашенная часть площади квадрата равна π/4.
|
Задание 5
|
После шторма прошлой ночью флагшток (вертикальный шест, на котором крепится флаг) на здании нашей школы наклонился. Если смотреть с северо-запада, его вершина находится справа от его нижней точки. Если смотреть с востока, то его вершина тоже будет правее его нижней точки. В каком из следующих направлений мог наклониться флагшток?

|
Правильный ответ: А
|
Ответ участника: А
|
Промежуточный результат: 35.25 + 3 = 38.25
|

На рисунке стрелками показаны направления взгляда с северо-запада и взгляда с востока. Правые полукруги от линии взгляда закрашены серым цветом. Некоторый сектор (тёмно-серый) оказался в двух полукругах. Согласно условию, вершина флагштока наклонилась в направлении этого сектора, что соответствует ответу А.
Задание 6
|
Прямоугольный лист бумаги имеет длину x и ширину y, где x > y. Лист можно свернуть двумя способами так, чтобы получилась боковая поверхность цилиндра. Чему равно отношение объёма более длинного цилиндра к объёму более короткого цилиндра?
A) y2 : x2
Б) y : x
В) 1 : 1
Г) x : y
Д) x2 : y2
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 38.25 - 0.75 = 37.5
|
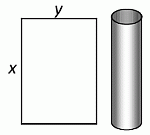
Найдём объём более длинного цилиндра (см. рис.). Его высота h = x, а радиус основания r такой, что 2πr = y, т.е. 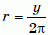 .
.
Тогда его объём 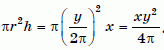
Аналогично, объём второго цилиндра
равен  .
.
Отношение этих объёмов равно 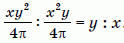 .
.
Задание 7
|
Пусть х = π/4. Какое из следующих чисел наибольшее?
A) x4
Б) x2
В) x
Г) √x
Д) 4√x
|
Правильный ответ: Д
|
Ответ участника: Д
|
Промежуточный результат: 37.5 + 3 = 40.5
|
Переобозначим x через a. Так как π = 3,14, то для x, а теперь для a: 0 < a < 1. При таком основании показательная функция y = ax убывает. Поэтому
a4 < a2 < a < √a < 4√a.
Видим, что наибольшим из чисел в вариантах ответа (поскольку a – это x) является число 4√x.
Задание 8
|
Сколько всего существует кратных 3 трёхзначных чисел, в записи которых участвуют только цифры 1, 3 и 5? (Одну и ту же цифру можно использовать несколько раз).
A) 3 Б) 6 В) 9 Г) 18 Д) 27
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 40.5 + 3 = 43.5
|
Согласно критерию делимости на 3, число делится на 3 тогда и только тогда, когда его сумма цифр делится на 3. Это условие заведомо выполняется, если у трёхзначного числа все цифры одинаковые. В нашем случае такими числами являются 111, 333, 555. Имеем 3 числа. Кроме того, сумма трёх цифр кратна 3, если они имеют разные остатки при делении на 3. В нашем случае это так, если все разрешённые цифры различны, т.е. число представляет собой перестановку цифр 1, 3 и 5. Число таких перестановок равно 6. Таким образом, всего существует 3 + 6 = 9 удовлетворяющих условию чисел.
Задание 9
|
Чему равна площадь треугольника на координатной плоскости с вершинами в точках (p; q), (3p; q) и (2p; 3q), где p, q > 0?
A) pq /2 Б) pq В) 2pq Г) 3pq Д) 4pq
|
Правильный ответ: В
|
Ответ участника: В
|
Промежуточный результат: 43.5 + 3 = 46.5
|
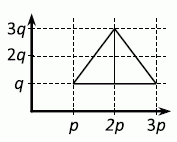
Построим на координатной плоскости данный треугольник (см. рис.). Видим, что он имеет горизонтальное основание длиной 3p – p = 2p; высота, проведённая к этому основанию, равна 3q – q = 2q. Поэтому площадь данного треугольника равна
0,5 · 2p · 2q = 2pq.
Задание 10
|
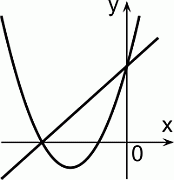
Парабола на рисунке имеет уравнение y = ax2 + bx + c при некоторых a, b и c. Какое из следующих уравнений может иметь прямая на рисунке?
A) y = bx + c
Б) y = cx + b
В) y = ax + b
Г) y = ax + c
Д) y = cx + a
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 46.5 + 3 = 49.5
|
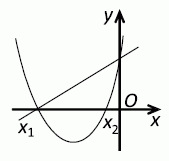
Из расположения данной параболы
y = ax2 + bx + c следует, что все коэффициенты в её уравнении положительны. Действительно, a > 0, так как ветви направлены вверх. Поскольку имеется два отрицательных корня x1 и x2, то, согласно формулам Виета,
b = –a(x1 + x2) > 0 и c = a · x1 · x2 > 0.
Теперь пусть данная прямая имеет уравнение А)
y = bx + c, и x1 – меньший из корней уравнения
y = ax2 + bx + c. Тогда имеем:
ax12 + bx1 + c = 0 и bx1 + c = 0, откуда ax12 = 0 . Так как x1 ≠ 0, получаем a = 0; противоречие.
Пусть уравнение прямой – Б) y = cx + b. Поскольку одна из точек пересечения прямой и параболы находится на оси ординат,
c · 0 + b = a · 02 + b · 0 + c. т.е. b = c. Тогда
x1 = -b/c = -1. Подставив это значение в уравнение параболы, получим a – b + c = 0, откуда a = 0; снова противоречие.
Пусть уравнение прямой – В) y = ax + b. Тогда, как и выше, b = c, и уравнения данных прямой и параболы можно переписать в виде
y = ax + c и y = ax2 + cx + c. Из первого уравнения x1 = -c/a. Подставив во второе уравнение, получим
a(-с/а)2 - с·с/а + с = 0, откуда c = 0; противоречие.
В случае Д) y = cx + a, как и раньше, получаем c = a. Поэтому уравнения данных прямой и параболы можно переписать в виде
y = ax + a и y = ax2 + bx + a. Из уравнения прямой находим x1 = –1. Подставив в уравнение параболы, получим
a – b + a = 0, откуда b = 2a. Тогда уравнение параболы имеет вид:
y = ax2 + 2ax + a, или y = a(x + 1)2. Но тогда оба корня x1 и x2 совпадают и равны –1; противоречие.
Видим, что только ответ Г) может быть правильным. В этом нетрудно убедиться непосредственно. Действительно, если y = ax + c, то
x1 = -с/а и а(-с/а)2 - b·с/а + с = 0 или
с2/а - b·с/а + с = 0. Разделив на c и умножив на a, получим:
с – b + a = 0, откуда b = a + c. Тогда уравнение параболы имеет вид
y = ax2 + (a + c)x + c.
Так как один корень x1 = -с/а и по формуле Виета произведение x1x2 = с/а, то x2 = -1.
В результате, если 0 < a < c и b = a + c, все условия выполняются.
Задание 11
|
Какую часть составляют нечётные делители числа 7! среди всех его делителей? (Запись n! обозначает произведение всех натуральных чисел от 1 до n.)
A) 1/2 Б) 1/3 В) 1/4 Г) 1/5 Д) 1/6
|
Правильный ответ: Г
|
Ответ участника: Г
|
Промежуточный результат: 49.5 + 4 = 53.5
|
Первое решение.
Запишем каноническое разложение числа:
7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 24 · 32 · 5 · 7.
Тогда каноническое разложение всякого делителя этого числа имеет вид
2l · 3n · 5m · 7k, где 0 ≤ l ≤ 4, 0 ≤ n ≤ 2, 0 ≤ m ≤ 1, 0 ≤ k ≤ 1. Так как показатели l, n, m и k могут принимать
соответственно 5, 3, 2 и 2 различных значения, количество всех делителей числа 7! равно 5 · 3 · 2 · 2 = 60. При этом делитель будет нечётным, если и только если l = 0. Поэтому количество нечётных делителей равно 3 · 2 · 2 = 12. Следовательно, нечётные делители среди всех делителей составляют 12/60 = 1/5 часть.
Второе решение.
Заметим, что 7! делится на 24, но не делится на бо́льшую степень 2. Теперь пусть d – нечётный делитель числа 7!. Тогда делителями числа 7! являются также 2d, 22d, 23d и 24d. Другими словами, на всякий нечётный делитель приходится 4 различных чётных делителя. Поэтому чётных делителей в 4 раза больше, чем нечётных. Значит, нечётные делители среди всех делителей составляют пятую часть.
Задание 12
|
Если A = (0; 1) ∪ (2; 3) и B = (1; 2) ∪ (3; 4), то чему равно множество всех чисел вида a + b, где a ∈ A, b ∈ B?
A) (1; 7)
Б) (1; 5) ∪ (5; 7)
В) (1; 3) ∪ (3; 7)
Г) (1; 3) ∪ (3; 5) ∪ (5; 7)
Д) другой ответ
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 53.5 - 1 = 52.5
|
Обозначим множество чисел вида x + y, где x ∈ X, y ∈ Y, через X + Y. Пусть (a, b) и (c, d) два числовых интервала (a < b и c < d). Докажем, что
(a, b) + (c, d) = (a + c, b + d). (*)
Поскольку a < x < b и c < y < d, то a + c < x + y < b + d. Следовательно, (a, b) + (c, d) ⊆ (a + c, b + d). Покажем, что имеет место и обратное включение.
Заметим сначала, что условие z ∈ (a, b) равносильно z = a + k(b – a) для некоторого 0 < k < 1. Действительно, из данного представления z находим
k = (z - а)/(b - а).
Причём условие a < z < b равносильно 0 < z – a < b – a, что, в свою очередь, равносильно
0 < (z - а)/(b - а) < 1.
Теперь пусть t ∈ (a + c, b + d). Тогда
t = a + c + k(b + d – a – c) для некоторого 0 < k < 1.
По-другому t = a + k(b – a) + c + k(d – c).
Положим x = a + k(b – a) и
y = c + k(d – c).
Тогда x ∈ (a, b), y ∈ (c, d) и t = x + y. Тем самым, имеем обратное включение
(a + c, b + d) ⊆ (a, b) + (c, d), и равенство (*) доказано.
Остаётся применить (*) для интервалов, из которых состоят множества
A = (0; 1) ∪ (2; 3) и B = (1; 2) ∪ (3; 4).
Получаем:
(0; 1) + (1; 2) = (1; 3),
(0; 1) + (3; 4) = (3; 5),
(2; 3) + (1; 2) = (3; 5),
(2; 3) + (3; 4) = (5; 7).
В результате A + B = (1; 3) ∪ (3; 5) ∪ (5; 7).
Задание 13
|
Сколько трёхзначных натуральных чисел обладает свойством: если цифры числа записать в обратном порядке, то получится число, на 99 большее исходного?
A) 8 Б) 64 В) 72 Г) 80 Д) 81
|
Правильный ответ: Г
|
Ответ участника: Б
|
Промежуточный результат: 52.5 - 1 = 51.5
|
Пусть abc = 100a + 10b + c – данное число. Согласно условию,
100c + 10b + a – (100a + 10b + c) = 99,
или 99c – 99a = 99,
или c – a = 1.
Значит, условию удовлетворяют числа вида 1b2, 2b3, …, 8b9 (8 типов). В каждом из типов цифра b может принимать 10 различных значений. Поэтому всего имеется 8 · 10 = 80 таких чисел.
Задание 14
|
Первые 1000 натуральных чисел записали в некотором порядке. Затем в каждой тройке подряд стоящих чисел вычислили их сумму. Какое наибольшее количество нечётных сумм могло получиться?
A) 997 Б) 996 В) 995 Г) 994 Д) 993
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 51.5 - 1 = 50.5
|
Заметим, что всего существует 998 сумм, о которых идёт речь. Покажем сначала, что все 998 сумм не могут быть нечётными. Для определения чётности суммы достаточно знать чётности слагаемых. Поэтому можно считать, что вместо чисел от 1 до 1000 в ряд в каком-то порядке записаны 500 чисел 1 (вместо нечётных) и 500 чисел 0 (вместо чётных). Кроме того, если в сумме есть два или три числа 1, то в этой сумме можно 1 + 1 заменить на 0. Чётность при этом не изменится. Другими словами, будем считать, что 1 + 1 = 0. Заметим
теперь, что если бы все суммы были нечётными, то наш ряд из 500 нулей и 500 единиц был бы периодическим с периодом 3. Действительно, если все суммы нечётные (т.е. равны 1 при нашем способе подсчёта) и если взять в этом ряду четыре подряд идущих числа a, b, c и d, то
a + b + c = b + c + d, откуда a = d.
Далее, сумма чисел в тройке будет нечётной, только если либо все три слагаемых равны 1, либо ровно одно слагаемое равно 1. Но в первом случае из-за периодичности все числа должны быть равны 1. А во втором случае количество чисел 1 в данном ряду либо 333 (если первое число 0), либо 334 (если первое число 1). Однако мы имеем 500 единиц; противоречие.
Итак, нечётных сумм не может быть 998. Покажем, что их может быть 997. Для этого достаточно построить пример. Сначала выпишем 225 троек (1, 0, 0) (будут исчерпаны все 500 чисел 0), после чего запишем оставшиеся
225 чисел 1. Мы получим:
…1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1… .
Здесь только одна тройка имеет чётную сумму (она подчёркнута). Таким образом, правильным является ответ 997.
Задание 15
|
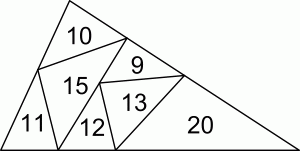
Треугольник разрезали на меньшие треугольники так, как показано на рисунке. Число внутри каждого меньшего треугольника указывает его периметр. Чему равен периметр исходного треугольника?
A) 31 Б) 34 В) 41 Г) 62 Д) другому числу
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 50.5 - 1 = 49.5
|
Если сложить периметры 10, 9, 20, 12 и 11 (всех тех треугольников, у которых есть стороны, лежащие на границе исходного треугольника), то получится периметр этого треугольника, увеличенный на сумму периметров 15 и 13 (двух внутренних треугольников). Следовательно, периметр данного треугольника равен
(10 + 9 + 20 + 12 + 11) – (15 + 13) = 34.
Задание 16
|
Обозначим через p(N) произведение цифр числа N. Например, p(23) = 2 • 3 = 6. Чему равна сумма
p(10) + p(11) + p(12) + … + p(99) + p(100)?
A) 2025 Б) 4500 В) 5005 Г) 5050 Д) другому числу
|
Правильный ответ: А
|
Ответ участника: Г
|
Промежуточный результат: 49.5 - 1 = 48.5
|
Сразу можно исключить из подсчёта слагаемые p(10), p(20) и т.д., так как они равны 0. Рассмотрим девятку чисел, у которых первая цифра равна n. Сумма произведений цифр таких чисел равна
n · (1 + 2 + 3 + ... + 9) = 45n.
Поэтому искомая сумма равна
1 · 45 + 2 · 45 + 3 · 45 + ... + 9 · 45 = (1 + 2 + 3 + ... + 9) · 45 = 45 · 45 = 2025.
Задание 17
|
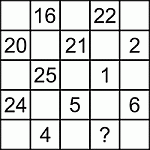
В каждую клетку квадрата 5 × 5 записано целое число. Некоторые из чисел показаны на рисунке, а некоторые скрыты. При этом, суммы чисел, стоящих во всех строчках и столбцах одинаковы. Какое число записано в клетке, отмеченной вопросительным знаком?
A) 8 Б) 10 В) 12 Г) 18 Д) 23
|
Правильный ответ: Б
|
Ответ участника: В
|
Промежуточный результат: 48.5 - 1 = 47.5
|
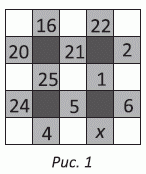
По условию, суммы чисел во всех строчках и столбцах одинаковые. Тогда сумма чисел в двух закрашенных строчках равна сумме чисел в двух закрашенных столбцах (см. рис.1). Опуская одинаковые слагаемые в этих суммах, расположенные на пересечениях рассматриваемых строчек и столбцов, получаем равенство
(20 + 21 + 2) + (24 + 5 + 6) = (16 + 25 + 4) + (22 + 1 + x), где x – искомое число.
Упрощая полученное уравнение, находим
43 + 35 = 45 + 23 + x , откуда x = 10.
В результате, чтобы найти правильный ответ, нам совсем не понадобилось заполнять все пустые клетки таблицы. Приведём всё же пример целиком заполненной таблицы, удовлетворяющей условию задачи.
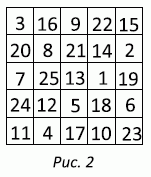
Это магический квадрат на рис.2. В его клетки вписаны числа от 1 до 25. Суммы чисел во всех строчках и всех столбцах, а также на двух диагоналях одинаковы и равны 65.
Задание 18
|
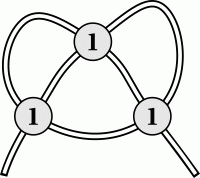
На столе лежит верёвка, частично закрытая тремя монетами, как показано на рисунке. Под каждой монетой верёвка может выглядеть как 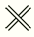 или
или  с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?
с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?
A) 1/2 Б) 1/4 В) 1/8 Г) 3/4 Д) 3/8
|
Правильный ответ: Б
|
Ответ участника: А
|
Промежуточный результат: 47.5 - 1 = 46.5
|
Поскольку виды перекрытий верёвки меняются на противоположные, если верёвку перевернуть, а наличие или отсутствие узла от этого не зависит, можно считать, что перекрытие под верхней монетой имеет вид  . Два других перекрытия могут быть любого вида. На рисунке ниже показаны все четыре возможных случая.
. Два других перекрытия могут быть любого вида. На рисунке ниже показаны все четыре возможных случая.

В первом и втором случае левая часть верёвки находится выше левого и верхнего перекрытий. Видим, что, если потянуть за правый конец верёвки, узел не образуется. В третьем случае, правая часть верёвки находится ниже правого и верхнего перекрытий. Если теперь потянуть за левый конец верёвки, то узел также не образуется. В четвёртом случае если двигаться вдоль верёвки, начав, например, с левого конца, положение верёвки при переходе через перекрытия каждый раз меняется (нижнее → верхнее → нижнее → верхнее → нижнее → верхнее). Поэтому в данном случае, если потянуть за концы верёвки, получим узел. Поскольку имеется 4 равновозможных случая и только в одном из них образуется узел, вероятность получить узел равна 1/4.
Задание 19
|

Вредный щенок схватил конец рулона бумаги и начал его тянуть с постоянной скоростью. Какой из приведённых ниже графиков функции лучше всего описывает толщину y рулона в зависимости от длины x развёрнутой части?

|
Правильный ответ: Д
|
Ответ участника: Б
|
Промежуточный результат: 46.5 - 1 = 45.5
|
Сначала исключим заведомо неверные ответы. Ясно, что при увеличении x толщина рулона y постоянно уменьшается. Поэтому ответы A и В – неверные. Кроме того, так как с увеличением x диаметр рулона уменьшается, скорость его вращения увеличивается. В результате толщина рулона уменьшается всё быстрее, т.е. с ускорением. Следовательно, ответы Б и Г также не являются верными. Остаётся ответ Д, который, по правилам конкурса, обязан быть верным.
В этом можно убедиться непосредственно. Найдём объём вытянутой части бумаги двумя способами. Если ширина бумаги равна h, толщина равна t (считаем, что она очень маленькая), длина вытянутой части равна x, то объём этой части (т.е. тонкого параллелепипеда) V = thx. Далее, рулон бумаги будем считать цилиндром (хотя это не совсем так: более точно, это своеобразная спираль). Поэтому, если начальный диаметр рулона равен d, а через некоторое время диаметр стал равен y, то
V = π/4·(d2 - y2)h (как
разность объёмов двух цилиндров). Из этих двух равенств получаем зависимость
tx = π/4·(d2 - y2),
или x = –ay2 + b, где

Данная зависимость – квадратичная, её графиком является парабола, что подтверждает правильность ответа Д.
Задание 20
|

На рисунке изображены три квадрата: PQRS, TRVU и UWXY. Точки P, T и X лежат на одной прямой. Площадь квадрата PQRS равна 36, а площадь TRVU равна 16. Чему равна площадь треугольника PXV?
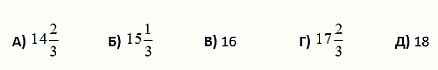
|
Правильный ответ: В
|
Ответ участника: Б
|
Промежуточный результат: 45.5 - 1 = 44.5
|
По условию, площадь квадрата PQRS равна 36, а площадь TRVU равна 16. Поэтому
их стороны равны соответственно 6 и 4. Обозначим сторону квадрата UWXY через a (см. рис. 1).

Поскольку точки P, T и X лежат на одной прямой, стороны треугольников PQT и TWX параллельны и, значит, эти треугольники подобны. Из подобия получаем:
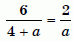 ,
,
откуда находим a = 2. Вычислим искомую площадь по схеме:
SPXV = SPXZS – SPSV – SVZX. Имеем:
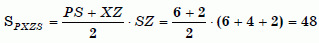 ,
,
 ,
,
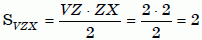 .
.
В результате SPXV = 48 – 30 – 2 = 16.
По-другому легко найти ответ, если построить аккуратный чертёж на клетчатой бумаге со стороной клетки 1 (см. рис. 2).

Видим, что SPXV = SPYZS – SPSV – SVZX – SPYX = 6 · 12 – 0,5 · 6 · 12 – 0,5 · 2 · 2 – 0,5 · 12 · 4 = 72 – 36 – 2 – 24 = 16.
Задание 21
|
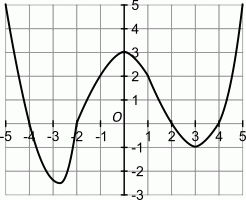
На рисунке изображён график функции f: [–5; 5] →  . Сколько различных решений имеет уравнение f(f(x)) = 0?
. Сколько различных решений имеет уравнение f(f(x)) = 0?
A) 2 Б) 4 В) 6 Г) 7 Д) 8
|
Правильный ответ: Д
|
Ответ участника: В
|
Промежуточный результат: 44.5 - 1.25 = 43.25
|
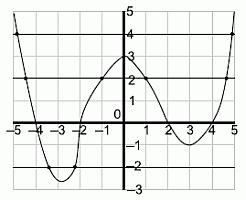
Из графика данной функции y = f(x) видно, что корнями уравнения f(x) = 0 являются числа –4, –2, 2 и 4.
Поэтому f(f(x)) = 0, только если либо f(x) = –4, либо f(x) = –2, либо f(x) = 2, либо f(x) = 4. Графически определить количество решений уравнения f(x) = a можно, если провести горизонтальную прямую y = a и найти количество её точек пересечения с графиком y = f(x). Соответствующие прямые изображены на рисунке. Видим, что количество их точек пересечения с графиком данной функции равно 8. Следовательно, уравнение f(f(x)) = 0 имеет 8 различных решений.
Задание 22
|
На доске были записаны числа 1, 2, 7, 9, 10, 15 и 19. Двое игроков по очереди стирали по одному числу, пока на доске не осталось только одно число. Сумма чисел, удалённых одним из игроков, оказалась в два раза больше суммы чисел, удалённых другим игроком. Какое число осталось?
A) 7 Б) 9 В) 10 Г) 15 Д) 19
|
Правильный ответ: Б
|
Ответ участника: Г
|
Промежуточный результат: 43.25 - 1.25 = 42
|
Пусть суммы чисел, удалённых игроками, равны S и 2S (по условию, одна сумма в 2 раза больше другой). Тогда сумма чисел, удалённых обоими игроками, равна 3S, т.е. кратна 3. Сумма всех семи данных чисел
1 + 2 + 7 + 9 + 10 + 15 + 19 = 63
также кратна 3. Следовательно, и число, которое осталось, обязано быть кратно 3. Среди данных чисел такими являются только числа 9 и 15. Покажем, что число 15 не могло остаться. Действительно, в противном случае, мы бы получили 3S = 63 – 15, откуда S = 16. Однако сумму 16 не дают никакие три из данных чисел (при этом нужно исключить из рассмотрения число 15). Итак, могло остаться только число 9. Легко привести и соответствующий пример. Если осталось число 9, то 3S = 63 – 9, откуда S = 18. Имеем:
1 + 7 + 10 = 18 и 2 + 15 + 19 = 36 = 2 · 18.
Задание 23
|
Функция f(x) такова, что f(1) = 2 и для любых x и y верно равенство f(x + y) = f(x) • f(y). Чему равно значение
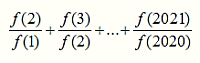 ?
?
A) 0 Б) 2021 В) 2 Г) 2020 Д) другому числу
|
Правильный ответ: Д
|
Ответ участника: нет ответа
|
Промежуточный результат: 42
В равенстве
f(x + y) = f(x) · f(y)
положим y = 1. Получим:
f(x + 1) = f(x) · f(1), откуда

при любом x. Тогда

|
Задание 24
|
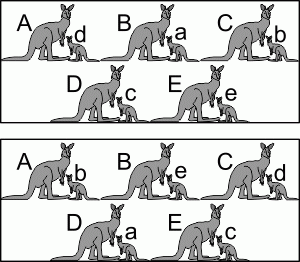
У пяти кенгуру с именами A, B, C, D и E есть по одному ребенку с именами a, b, c, d и e. На первом групповом фото ровно двое кенгурят стоят рядом со своими мамами. На втором фото ровно трое кенгурят стоят рядом со своими мамами. Чьим ребенком является кенгурёнок а?
A) A Б) B В) C Г) D Д) E
|
Правильный ответ: Г
|
Ответ участника: В
|
Промежуточный результат: 42 - 1.25 = 40.75
|
Изобразим пары, указанные на рисунках в условии задачи, в виде графа. Вершинами графа будут кенгуру-мамы и кенгуру-дети. Если какие-то кенгуру-мама и кенгурёнок находятся в паре на первом рисунке, то соединим соответствующие вершины сплошной линией, а если они находятся в паре на втором рисунке, то соединим штриховой линией. Эти линии будем называть рёбрами. Таким образом, в графе из каждой вершины должно выходить ровно два ребра: одно сплошное и одно штриховое. Такой граф представляет собой цикл или объединение непересекающихся циклов. Его можно изобразить так, что рёбра не будут иметь пересечений.

В нашем случае (см. рис.) граф является объединением двух циклов: короткого (4 вершины) и длинного (6 вершин). Далее, если пару образуют родные мама и ребёнок, то такую пару и соответствующее ребро будем называть правильными, в противном случае – неправильными. Согласно условию, на графе 5 правильных рёбер: 2 сплошных и 3 штриховых. Число неправильных рёбер тоже равно 5. Заметим, что правильные рёбра не могут быть соседними, т.е. выходить из одной вершины. Иначе это бы означало, что у какого-то кенгурёнка две мамы, или у какой-то мамы два родных кенгурёнка. По условию, это не так. Следовательно, правильные и неправильные рёбра в каждом цикле чередуются. Поэтому в каждом цикле они изображены одинаковыми линиями: либо сплошными, либо штриховыми. Ровно два сплошных ребра имеется в коротком цикле, а ровно 3 штриховых – в длинном цикле. Они и являются правильными. В частности, ребро a-D – правильное. Это значит, что кенгурёнок a является ребёнком кенгуру-мамы D.
Задание 25
|
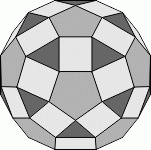
Многогранник на рисунке имеет 12 правильных пятиугольных граней, а остальные грани – либо равносторонние треугольники, либо квадраты. Каждая пятиугольная грань окружена пятью квадратными гранями, а каждая треугольная грань окружена тремя квадратными гранями. Ваня записал число 1 на каждой треугольной грани, число 5 на каждой пятиугольной грани и число -1 на каждой квадратной грани. Чему равна сумма чисел на всех гранях данного многогранника?
A) 20 Б) 50 В) 60 Г) 80 Д) 120
|
Правильный ответ: Б
|
Ответ участника: Д
|
Промежуточный результат: 40.75 - 1.25 = 39.5
|
Задача заключается в том, чтобы найти число квадратных и число треугольных граней данного многогранника. После этого сумма чисел на гранях вычисляется элементарно.
По условию, имеется 12 пятиугольников. У каждого пятиугольника 5 соседних (по общей стороне) квадратов. Но у каждого квадрата ровно по 2 соседних пятиугольника. Поэтому число квадратов равно (12 ⋅ 5) : 2 = 30. Далее, у каждого квадрата 2 соседних треугольника. Но каждый треугольник является соседним для 3 квадратов. Поэтому число треугольников равно (30 ⋅ 2) : 3 = 20. В результате сумма чисел на всех гранях данного многогранника равна
12 ⋅ 5 + 30 ⋅ (−1) + 20 ⋅ 1 = 50.
По-другому найти число квадратов и треугольников можно, если рассмотреть вершины данного многогранника. Заметим, что каждая вершина является вершиной одного из пятиугольников. Поэтому число вершин равно 12 · 5 = 60. С другой стороны, каждая вершина является вершиной одного треугольника. Поэтому, если t – число треугольников, то число всех вершин равно 3t. Наконец, каждая вершина является вершиной ровно двух квадратов. Поэтому, если k – число квадратов, то число всех вершин равно 4k : 2 = 2k. Получаем двойное уравнение 3t = 2k = 60, откуда k = 30 и t = 20. Далее, аналогично вычисляем сумму чисел на гранях.
Ещё один способ получить уравнения для нахождения t (числа треугольников) и k (числа квадратов) состоит в том, чтобы по-разному подсчитать число рёбер данного многогранника. Как и выше, замечаем, что число вершин равно 60. Из каждой вершины выходит ровно 4 ребра, но каждое ребро связывает две вершины, являющиеся его концами. Поэтому число рёбер равно (60 · 4) : 2 = 120. С другой стороны, каждое ребро является ребром ровно одного квадрата. Поэтому число рёбер равно 4k. Наконец, каждое ребро является либо ребром пятиугольника, либо ребром треугольника. Поэтому число рёбер равно 5 · 12 + 3t. Из двойного уравнения 60 + 3t = 4k = 120 снова находим: k = 30 и t = 20.
Отметим в заключение, что многогранник в данной задаче называется ромбикосододекаэдром. Он является одним из 13 полуправильных архимедовых многогранников, впервые был описан в 4 веке нашей эры.
Задание 26
|
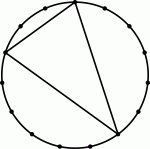
На окружности через равные промежутки отмечено 15 точек. Сколько существует попарно не равных треугольников с вершинами в этих точках?
A) 19 Б) 91 В) 46 Г) 455 Д) 23
|
Правильный ответ: А
|
Ответ участника: В
|
Промежуточный результат: 39.5 - 1.25 = 38.25
|
Первое решение.
Число способов выбрать 3 вершины из 15, а значит, число всех треугольников с вершинами в данных точках, равно

Среди них имеется 5 равносторонних треугольников, которые равны друг другу, потому считаем их за 1. Среди оставшихся 455 – 5 = 450 треугольников имеется 6 различных равнобедренных (при фиксированной вершине равнобедренного треугольника есть 6 способов выбрать его основание). Из каждого такого треугольника можно получить 15 равных ему треугольников при поворотах по кругу. Это в общей сложности даёт 6 · 15 = 90 треугольников, которые мы считаем за 6. У остальных 450 – 90 = 360 треугольников все стороны разные. Они тоже переходят в 15 равных им треугольников
при поворотах. Кроме того, они переходят в равные треугольники и в результате 15 симметрий относительно прямых, проходящих через центр окружности и одну из отмеченных точек. Последние треугольники имеют другую
круговую ориентацию, по сравнению с теми, которые получаются при поворотах (повороты круговую ориентацию не меняют). Поэтому среди оставшихся 360 треугольников существует 360 : (15 + 15) = 12 неравных друг другу треугольников. В результате, всего получаем 1 + 6 + 12 = 19 различных треугольников.
Второе решение.
Окружность делится отмеченными
точками на 15 дуг по 360° : 15 = 24° градуса каждая. Углы рассматриваемых треугольников вписаны в окружность и опираются на одну или несколько таких дуг. Поэтому углы рассматриваемых треугольников равны или кратны 24° : 2 = 12°. Итак, углы всех рассматриваемых треугольников (в градусах) равны 12n, 12m и 12k для некоторых натуральных n, m и k, причём 12n + 12m + 12k = 180, откуда n + m + k = 15. В данной ситуации рассматриваемые треугольники равны тогда и только тогда, когда их углы равны. Поэтому число различных треугольников среди них равно количеству различных разбиений числа 15 на три натуральных слагаемых, порядок следования которых неважен.
Следует отметить, что задача нахождения числа разбиений натурального числа N на конкретное (или произвольное) число слагаемых является важной, но непростой задачей комбинаторики и теории чисел. Однако в нашем случае, учитывая, что 15 – небольшое число, можно выписать все возможные разбиения непосредственно. Сделаем это систематически. Будем записывать слагаемые в порядке неубывания. При этом сначала выпишем группу всех разбиений с первым слагаемым равным 1, последовательно увеличивая второе слагаемое, затем группу с первым слагаемым 2 и т.д. Вот, что получим:
1+ 1 + 13,
1 + 2 + 12,
1 + 3 + 11, ...,
1 + 7 + 7,
2 + 2 + 11,
2 + 3 + 10, ...,
2 + 6 + 7,
3+ 3 + 9, ...,
3 + 6 + 6,
4 + 4 + 7,
4 + 5 + 6,
5 + 5 + 5.
Число записанных разбиений равно
7 + 5 + 4 + 2 + 1 = 19.
Задание 27
|
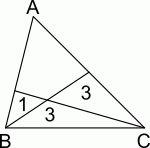
Треугольник ABC разбит на четыре части двумя отрезками, как показано на рисунке. Площади треугольных частей равны 1, 3 и 3. Чему равна площадь исходного треугольника?
A) 12 Б) 12.5 В) 13 Г) 13.5 Д) 14
|
Правильный ответ: А
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Разобьём дополнительно четырёхугольную часть на два треугольника так, как показано на рисунке.
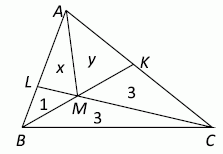
Пусть их площади равны x и y. Из того, что площади треугольников BMC и MKC равны, следует, что BM = MK. А из этого равенства, в свою очередь, следует, что площади треугольников BAM и MAK равны, т.е. x + 1 = y. Аналогично, поскольку площади треугольников BLM и BMC относятся как 1 : 3, то так же относятся
длины отрезков LM и MС. А из этого, в свою очередь, следует, что так же относятся площади треугольников ALM и MAC, т.е. 3x = y + 3. Последнее уравнение с учётом полученного ранее можно переписать в виде 3x = x + 4, откуда x = 2, и тогда y = 3. В результате площадь треугольника ABC равна
1 + 3 + 3 + 2 + 3 = 12.
|
Задание 28
|
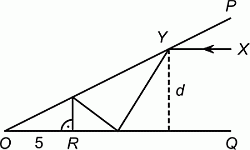
Два плоских зеркала OP и OQ наклонены под острым углом (см. рис.). Луч света XY, параллельный QO, падает на зеркало OP в точке Y. После этого он отражается и попадает на зеркало OQ, повторно отражается и снова попадает на зеркало OP. После третьего отражения луч попадает под прямым углом на зеркало OQ в точку R. Известно, что OR = 5. На каком расстоянии d от зеркала OQ находится точка Y?
A) 4 Б) 4.5 В) 5 Г) 5.5 Д) 6
|
Правильный ответ: В
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Пусть зеркала наклонены под углом α. Тогда, согласно условию, первый раз луч падает на зеркало OP и отражается от него тоже под углом α (см. рис.1).

Пусть β – угол следующего падения (и отражения) на зеркало OP в точке T. Согласно условию, TR ⊥ OQ. Поэтому треугольник OTR – прямоугольный. А тогда и подобный ему (по углам α и β) треугольник TZY также прямоугольный. То есть ∠TZY = 90°. Тогда на углы ∠TZR и ∠YZD (падения и отражения в точке Z) также приходится 180° – 90° = 90° и, значит, они равны 45°. Пусть TR = a. Тогда в прямоугольном равнобедренном треугольнике TRZ гипотенуза TZ = a√2, а в прямоугольном равнобедренном треугольнике ZYD гипотенуза ZY = d√2. И из подобия треугольников OTR и TZY получаем:
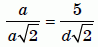 , откуда d = 5.
, откуда d = 5.
Немного по-другому можно получить ответ с помощью тригонометрии. Пусть углы падения и отражения луча равны α, β и γ, как показано на рис.2.

Тогда снова, легко видеть, треугольник TZY – прямоугольный. Последовательно рассматривая справа налево имеющиеся прямоугольные треугольники, находим:
d = YD = ZY · sinγ = TZ · ctgα · sinγ = TR · ctgα = OR = 5.
Приведём ещё одно решение.
Пусть зеркала наклонены под углом α, и тогда α – первый угол падения и отражения. Заметим, что каждый следующий угол падения и отражения увеличивается
на α (см. рис.3).

Действительно, угол ∠YZD, как внешний для треугольника OYZ, равен ∠OYZ + ∠YOZ = 2α. Далее, аналогично ∠YTZ = ∠TOZ + ∠OZT = α + 2α = 3α и ∠TRD = ∠TOR + ∠OTR = α + 3α = 4α. Согласно условию, 4α = 90°. В частности, треугольник TZY – прямоугольный. Пусть TZ'Y – симметричный ему треугольник относительно прямой OP. Легко видеть, что четырёхугольник OZYZ' – ромб и △ZYD = △Z′YR . Тогда в прямоугольном треугольнике ZYD имеем: ZD = OR = 5 и ∠YZD = 2α = 45°. Поэтому он равнобедренный и, значит, d = YD = ZD = 5.
|
Задание 29
|
Пусть M(k) – максимальное значение выражения |4x2 – 4x + k| при x ϵ [–1; 1], где k –произвольное действительное число. Чему равно наименьшее возможное значение M(k)?
A) 4 Б) 9/2 В) 5 Г) 11/2 Д) 8
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Графиком функции y = 4x2 – 4x является парабола. Легко подсчитать, что абсцисса её вершины xв = 0,5.
График функции y = 4x2 – 4x + k получается сдвигом данной параболы по вертикали на величину k.
Если все значения функции y = 4x2 – 4x + k неотрицательны, то её график является также графиком функции y = |4x2 – 4x + k|. В противном случае, чтобы получить график y = |4x2 – 4x + k| из параболы y = 4x2 – 4x + k, нужно всю её часть, расположенную ниже оси абсцисс, отразить симметрично относительно этой оси.
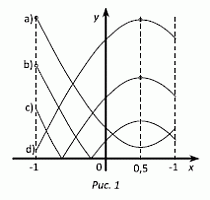
На рис.1 приведены возможные варианты
графика на отрезке [–1; 1] при различных значениях k. Видим, что максимальное значение функции y = |4x2 – 4x + k| на отрезке [–1; 1] достигается либо в вершине параболы, т.е. при x = 0,5, либо на конце данного отрезка, точнее, на левом конце (в силу того, что он находится дальше от абсциссы вершины, чем правый) т.е. при x = –1. Соответствующие точки максимума обозначены на графиках. Значение |4x2 – 4x + k| при x = –1 равно |k – 1|, а при x = –1 равно
|k + 8|. Поэтому M(k) = max{|k – 1|, |k + 8|}.
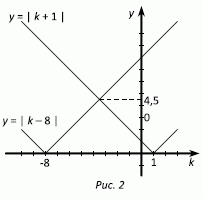
На рис.2 приведены графики функций y = |k + 8| и y = |k – 1|. График функции y = M(k) получится, если при всех значениях k из двух соответствующих точек этих графиков выбрать ту, которая выше. Поэтому он имеет V-образный вид, и наименьшее значение достигается в точке пересечения графиков на рис.2. Несложные вычисления показывают, что оно равно 4,5, или 9/2.
|
Задание 30
|
В некоторой игре, чтобы выиграть, нужно опередить другого игрока на 3 очка. Два игрока A и B играют в такую игру и в некоторый момент игрок A опережает игрока В на 1 очко. Игроки имеют одинаковую вероятность выиграть каждое следующее очко. Какова вероятность того, что А выиграет игру?
A) 1/2 Б) 2/3 В) 3/4 Г) 4/5 Д) 5/6
|
Правильный ответ: Б
|
Ответ участника: нет ответа
|
Промежуточный результат: 38.25
Будем говорить, что на данном этапе произошло событие A, если на этом этапе А получил 1 очко, и, соответственно, событие B, если B получил 1 очко. По условию, эти события не зависят от результатов на предыдущих этапах и равновозможны, т.е. имеют вероятность 1/2. Далее, игрок А имеет на 1 очко больше, чем B. Для того чтобы ему победить в игре, нужно получить ещё на 2 очка больше, чем B. Пусть искомая вероятность равна p. События AA, AB, ВA и ВВ образуют полную группу результатов следующих двух игр. Они равновозможны и имеют вероятности 1/4. В первом случае A уже победил (вероятность победы равна 1), во втором и третьем случае он попрежнему опережает противника на 1 очко (вероятность победы равна p), в четвёртом случае игрок B опережает A на 1 очко (вероятность того, что победит B, равна p, а значит, вероятность победы A равна 1 – p). По формуле полной вероятности имеем:
p = 1/4 ⋅ 1 + 1/4 ⋅ p + 1/4 ⋅ p + 1/4 ⋅ (1 - p).
Упрощая, получим 4p = 1 + p + p + 1 − p , откуда p = 2/3.
Немного по-другому задачу можно решить так. Снова, пусть искомая вероятность равна p. Если после того, как A опережает соперника на 1 очко, В выиграет 1 очко (вероятность этого равна 1/2), то у них очков поровну. Следовательно, после этого вероятность одержать окончательную победу для A равна 1/2. Если же после того, как A, имея превосходство в 1 очко, выигрывает ещё 1 очко (вероятность 1/2), то ситуация следующая. На очередном этапе он может снова выиграть очередное очко с вероятностью 1/2 и в результате одержать окончательную победу. Либо 1 очко выиграет B (вероятность 1/2). Тогда A будет опережать его по-прежнему на 1 очко, вероятность одержать после этого окончательную победу равна p. По формуле полной вероятности имеем:
p = 1/2 ⋅ 1/2 + 1/2 ⋅ 1/2 ⋅ 1 + 1/2 ⋅ 1/2 ⋅ p, откуда снова p = 2/3.
|








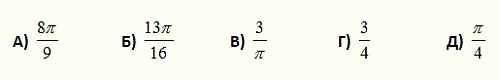



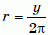 .
.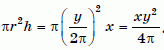
 .
.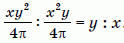 .
.







 или
или  с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?
с одинаковой вероятностью. С какой вероятностью образуется узел, если потянуть за концы этой верёвки?




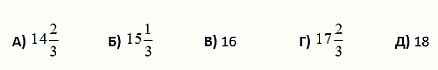

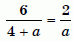 ,
,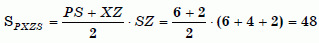 ,
, ,
,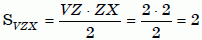 .
.

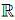 . Сколько различных решений имеет уравнение f(f(x)) = 0?
. Сколько различных решений имеет уравнение f(f(x)) = 0?
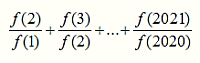 ?
?










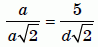 , откуда d = 5.
, откуда d = 5.



